高阶滑模控制
高阶滑模控制
定义和思想
为什么使用高阶滑模控制
传统的滑模控制针对大范围的控制问题,在具有不确定因素的条件下,已经可以提供鲁棒、高精度的控制效果,但其还存在 2 个限制
- 在滑模面上的约束方程只能具有 1 的 relative degree ,这意味着控制量显示的出现在约束方程的第一阶导数中
- 控制量会出现高频的 chattering,这是在实际应用中很难接受的
基本实现
简要性质证明
- 滑模控制 有下面几点好处:
- robustness
- parameter variations
- reduced order dynamics
高阶滑模控制保持了滑模控制的多数好处,其是一阶滑模控制的推广延伸
相比于传统的滑模控制,高阶滑模控制影响的是滑模变量的高阶导数,而非仅仅传统的
- 比如:
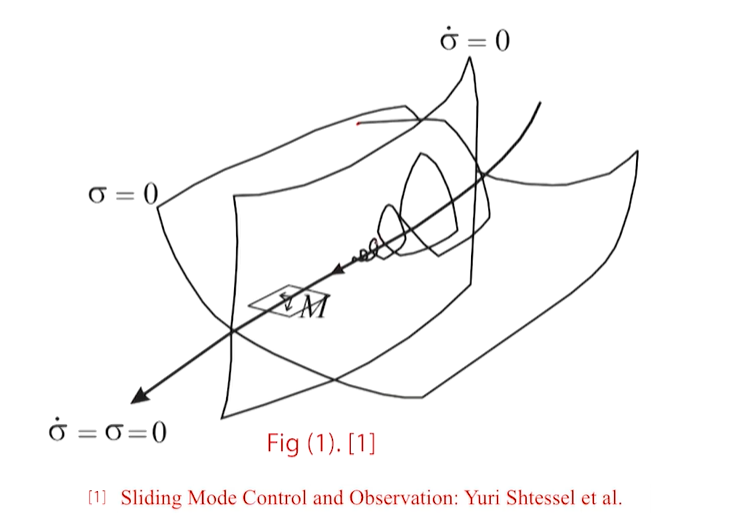
note
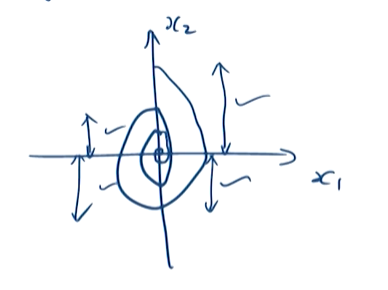
状态轨迹有限时间收敛
参考引文 1 完成证明
note
证明的主要思想:证明相轨线距离原点的距离在“逐渐”缩短。图中示意的是轴线上的距离逐渐变短
给定下面这样的示意系统:
^eqn-system
设计输入为:
^eqn-control-law
收敛性
分析设计的滑模控制器在相图中的轨迹变化情况
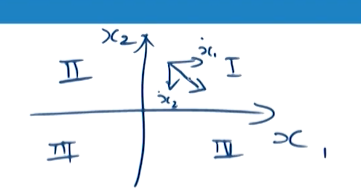
第一象限
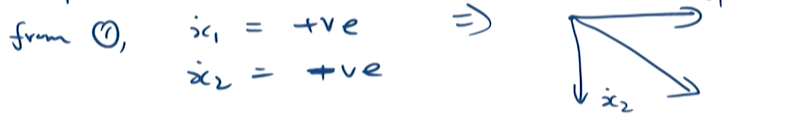
第四象限

第三象限
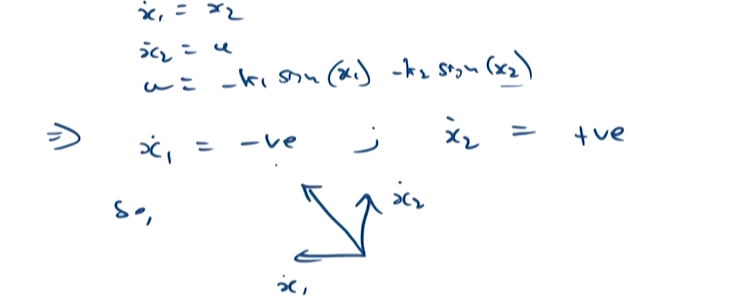
第四象限
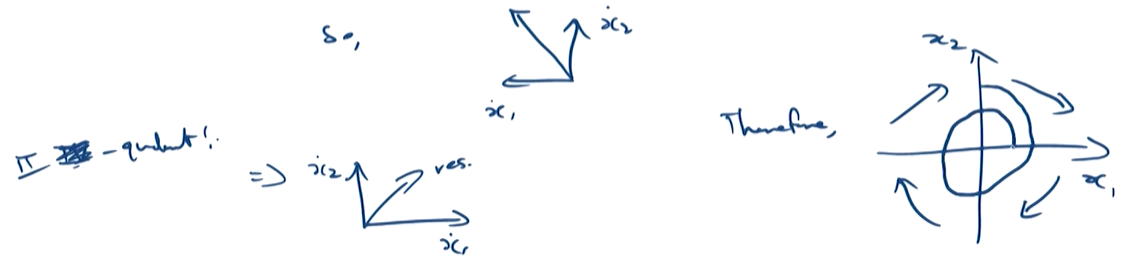
上面的分析表明会行程上面的螺线,下面证明会收敛
根据 ^eqn-system 和 ^eqn-control-law^eqn-control-law,又由于滑模变量 有:
看到上面这个式子,很常见的一个想法是:
因此有:
根据 第一象限 的分析,有:
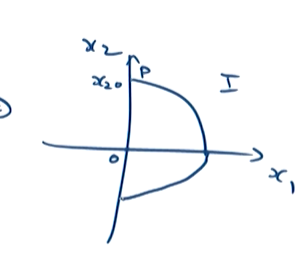
类似的,考虑 第四象限 的分析,有:
这意味着在 轴向距离逐渐缩短
其余的基本类似
有限时间
证明了收敛性,下面考虑有限时间收敛性质
注意到在第一象限,由于 ^eqn-control-law,而 u 直接控制 ,因此:
在第四象限,类似的,有:
总时间为:
note
注意这里考虑的是总时间,从对称性角度考虑的
类似的,有:
从而表明,根据数列收敛的性质表明有限时间收敛
备注
滑模控制的创始人之一 utkin 于 2016 年 3 月在 IEEE TAC 刊出的“Discussion aspects of high order sliding mode control”一文中全面的质疑了高阶滑模控制对于传统滑模控制的优越性,包括相对阶问题,有限时间收敛性,抖振问题,应用前景等 @utkinDiscussionAspectsHighOrder2016
Super-twisting[1] [2] 也是高阶滑模控制的一种,本来想研究一番的,但是看了这个知乎问题和对应的论文之后,有点怵,感觉是个坑,因为没有这方面的项目,所以就不深挖了 x。
参考
引文
脚注
On Convergence Time and Disturbance Rejection of Super-Twisting Control," in IEEE Transactions on Automatic Control, vol. 58, no. 8, pp. 2013-2017, Aug. 2013, doi: 10.1109/TAC.2013.2251812 ↩︎