控制系统中带宽的理解
控制系统中带宽的理解
控制系统中带宽的理解
定义
带宽频率
闭环截止频率,指当闭环幅频特性下降到频率为 0 时的 分贝 值以下 3dB 时,对应的频率,记为 。
开环截止频率
也成为剪切频率,是闭环系统的开环幅频特性中,幅频特性曲线穿越 0dB 线的频率,记为 。
开环截止频率与闭环截止频率具有同向性
对一个闭环控制系统而言,其开环截止频率与闭环截止频率是两个完全不同的物理量,但他们之间存在一定的相关性,即:开环截止频率与其单位负反馈的闭环截止频率是通向增大的,且具有关系 。
例子
首先介绍一个例子说明截止频率对系统性能的影响,在总结带宽对系统的影响。
以经典的弹簧阻尼系统为例,首先有动力学方程:
即有:惯性力 + 阻尼力 + 弹性力=外界激励
具体赋值为:b= 为阻尼系数, 为弹性系数,因此写成传递函数形式为:
使用一个交变的正弦力 去激励系统,有响应为: 频率不变的正弦结果,改变的只是幅值、相位 (原因为 这种形式的解为拉普拉斯变换对应的特征值,自然界规定的)。对应的图像如下:
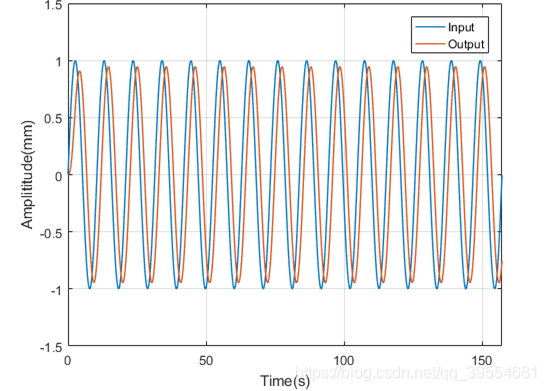
进一步修改频率,改变的也只有信号的幅值和相位:
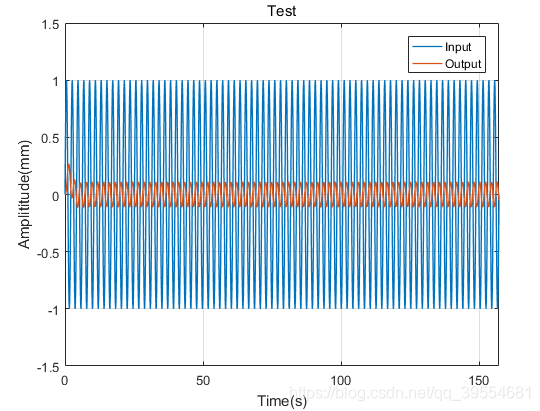
对于系统,绘制其 Bode 图 如下:
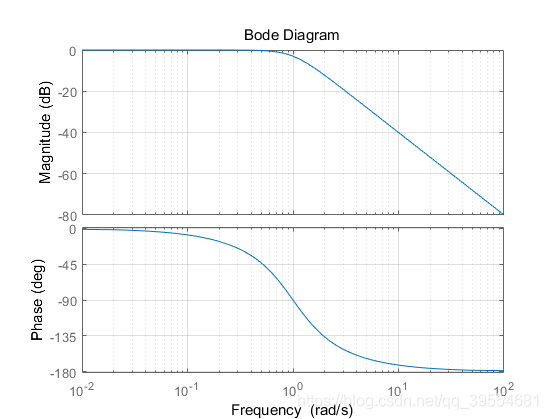
可以发现,在频率小于 1rad/s 时,系统的频率响应增益基本为 1,也就是幅值和输入基本一致,相位落后为 0-90 deg。当频率大于 1rad/s 时,幅值响应迅速衰减,当频率增加至 100rad/s 时,幅值响应为 -40dB,也就是输入幅值的 ,相位基本落后到 180deg.
由此可见,对于一个一般的 线性时不变系统,系统具有低通特性。参考 信号 的定义,-3dB 对应于幅值缩小 ,低于这个频率的认为信号可以通过,高于的认为存在大幅度的信号过滤。特别的,对于一个 二阶系统,当阻尼比 时,系统的自然频率 代表了截止频率。 ^6f74f1
举个例子,输入存在 2 个正弦函数,为 ,一个分量是截止频率的 1/2,另一个是截止频率的 10 倍,对应的结果为:
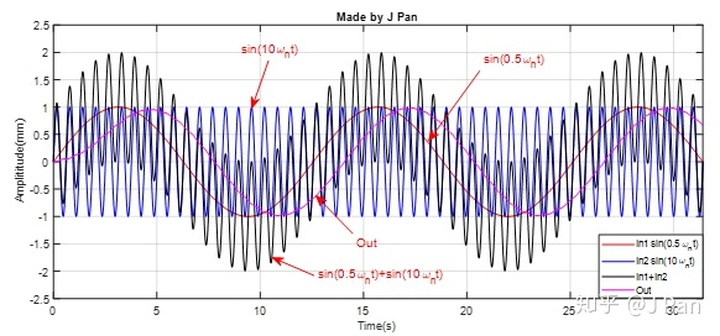
可以发现, 的份量可以比较好的通过。
更进一步,对于更加复杂的输入,响应如何?
对于 常见信号,可以知道其频谱分布在整个频率轴上,且随着频率增加而减小。
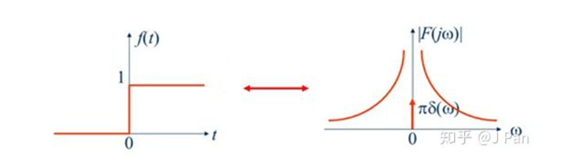
得到系统的阶跃响应为:
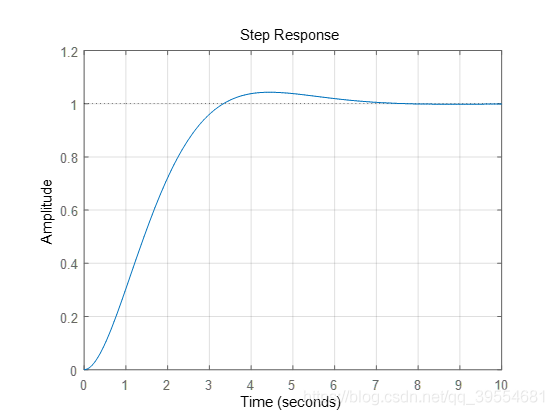
总体来说,基本曾献阶跃信号特点。加入改变系统的截止频率,使得
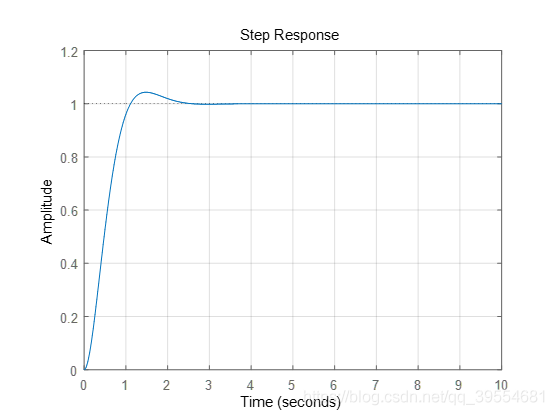
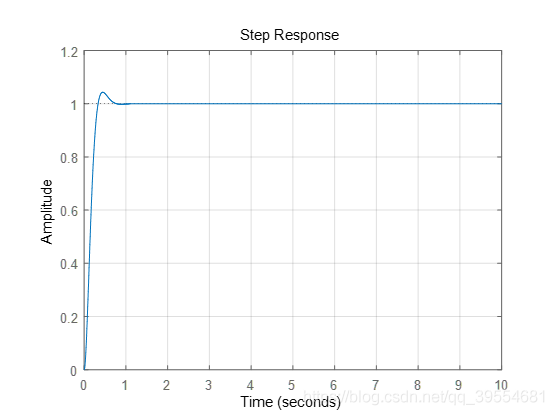
可以发现,随着截止频率增加,越来越多频率的信号可以通过系统,输出更加接近输入信号 (^6f74f1)。
基于的是 LTI 系统一般是低通。比如静态增益不是 1 的,或者是高阶的系统,对低频出现了放大,这导致和原始信号不同了
控制系统种一般闭环系统比较多,对闭环系统而言,其截止频率就等于带宽。从时域的角度来看,系统的带宽越大,时域的响应速度也越快,系统跟踪输入信号的能力越强;带宽无穷大时,系统可以完全“复现”输入信号,当然物理不可以实现。