基本滑模控制简介和示例
基本滑模控制简介和示例
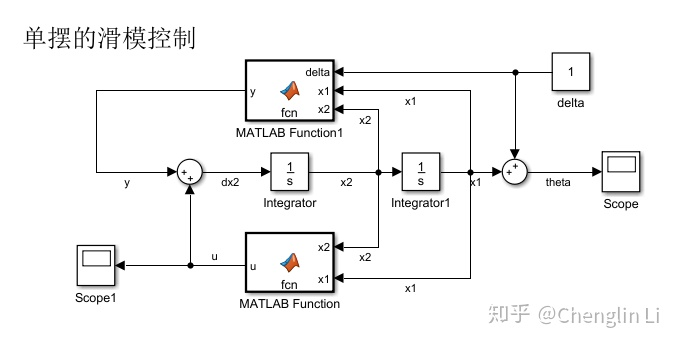
基本滑模控制
定义
滑模控制是在控制系统相空间下考虑实现的一种控制方法,相当简单且控制性能优越,具有以下优点:
- 滑动模态可以进行设计。调节的参数少,响应速度快。
- 对扰动不灵敏。滑模控制对扰动有很强的抑制能力,这对于在复杂环境工作下的机器来说非常友好。
滑模控制本质上是一种非线性控制手段,简单来说,其非线性表现为控制的不连续性,也即系统的结构不固定,可以在动态的过程中根据系统当前状态有目的地不断变化,迫使系统按照设计的“滑模面”的状态轨迹进行运动。
用一个例子进行介绍:假设在一个光滑的平面上有小木块,他在坐标 X=2 处,其存在一个初始速度 v 向着坐标轴反方向运动,目的是设计一个控制器,使其能够最后停在坐标原点。
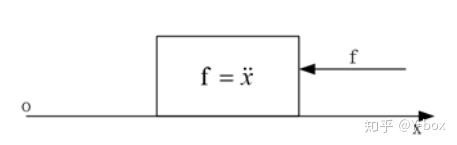
写出系统状态方程
其中 代表物体的位置, 代表物体的速度,u 代表控制器的输出,也就是作用力 f。控制目标是使得物体停在坐标原点,即 。
设计滑模面
滑模面是什么?可以看成在物体相空间内的一个流行,这里简单来说是一个平面。这样设计是为什么呢?
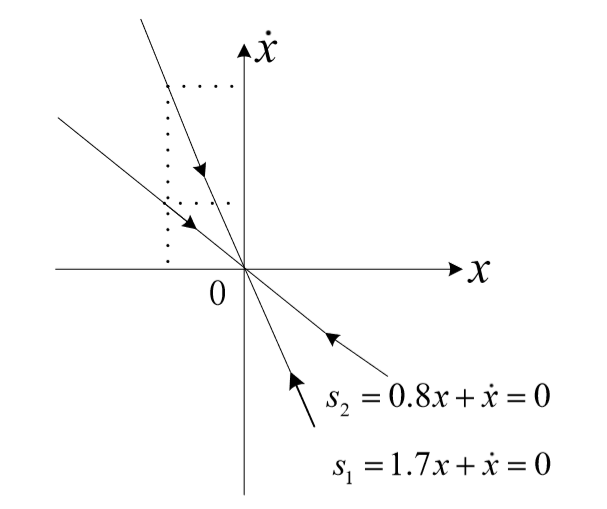
之前我们设计控制器的目的是使得 ,考虑在设计的滑模面上物体的运动:
可以发现,这样的设计使得状态量都会趋近于 0,并且以指数形式趋近,这可能是滑模面中模态的意义——特征值引起的指数收敛。用相平面表示这个趋近过程如下图:
设计趋近律,寻找 s 与控制 u 之间的关系
上面介绍了设计选取滑模面 s,因此需要对控制律进行设计使系统在滑模面上运行。
由于 ,因此有:
由于设计的滑模面是一个平面,线性的结构使得控制律 u 可以通过趋近律 控制,一般可以这样设计:
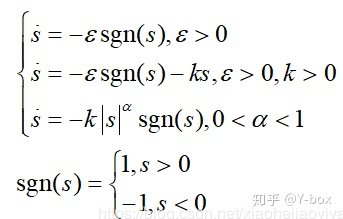
根据上面设计的趋近律可以求出控制器 u 的表达式。e.g. ,有:,对木块施加这样的 u 的控制,可以使得木块稳定在原点。
为什么如此选取控制律可以使得 s=0?
在控制原理中,我们经常使用 李雅普诺夫稳定性 来对系统的稳定性进行判断,特别的其中使用 Lyapunov 函数作为判据。
对当前的系统,我们关心的是 s 是否能在我们给定的控制律下保持为 0,即对于控制系统,以 s 作为变量,使用 Lyapunov 函数进行判断。其判定方法为:对于一个 s 为变量的系统,如果存在一个连续函数 V 满足:
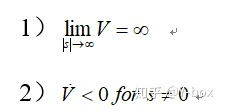
那么系统可以在平衡点 s=0 处稳定。
设计李雅普诺夫函数 ,显然对第一个条件满足。对于第二个条件,,因此也满足第二个条件。根据李雅普诺夫判据,s 会最终稳定于滑模面,使得 s=0。
总结一下滑模控制的设计步骤
首先根据被控对象的状态方程设计滑模面,状态一旦到达滑模面 ,,将以指数趋近方式达到稳定状态。然后设计趋近律求出控制器的表达,李雅普诺夫函数作为稳定性的保证,即保证 s=0 可达,(相平面中的其他点能到达滑模面)。
一些问题和改进
控制问题除了保证其能够收敛,还需要考虑响应时间,尽管之前的李雅普诺夫函数保证了 s 最终会稳定于 0,但并没有保证什么时候到达,这对控制系统是没有意义的。
因此对 Lyapunov 函数的第二个条件 (相平面点可达性) 进行修改,让他能够有限时间到达稳定点。
对于改进后的第二个条件,分离变量后积分,假设积分时间为 t,有:
进一步得到收敛时间 满足
因此,由于李雅普诺夫条件的改变,控制器 u 也要发生相应的改变:
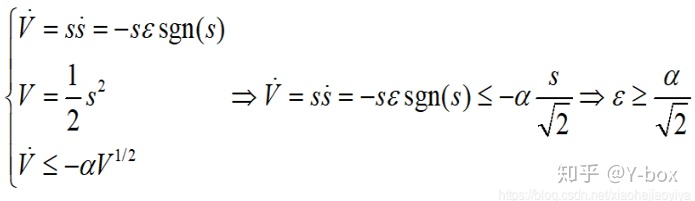
只有满足 才能使得有限时间到达滑模面。
对于干扰项的响应
加入干扰项后,有新的状态方程:
干扰项引入并不影响滑模面设计,仍然有:,变化的是趋近律 ,有:,控制律 u 满足上面不考虑 d 的形式: 。
为了满足李雅普诺夫函数,有:
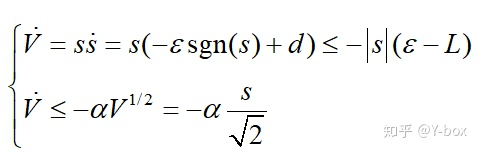
其中 L 表示干扰的上届,d<L。对比上面的条件,因此有 时 Lyapunov 函数既满足有限时间收敛又负定。因此,系统仍按照先滑动到滑模面,再沿滑模面做指数趋近运动。干扰没有对系统造成影响 ^78b303
^78b303 是否应为:
Formal 的介绍
考虑二阶系统
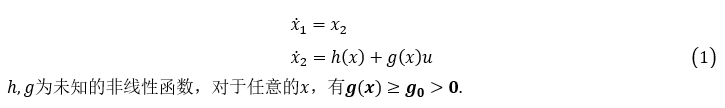
u 是控制律,控制目的:设计一个状态反馈控制器以稳定原点。
控制方法和思路:


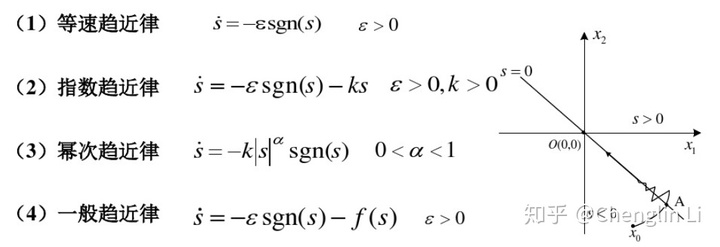
2 滑动曲面


3 滑模面设计

4 抖动现象
由于实际系统中开关器件和继电器的非理想性,或者由于惯性、滞后的因素存在,使得滑模控制常常出现抖动。
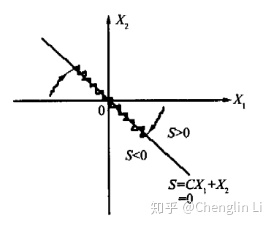
(1)消除抖动的方法一:将控制分解为连续控制和切换控制两部分,以减少切换部分的幅度。
(2)方法二:采用陡峭的饱和函数,代替符号函数。 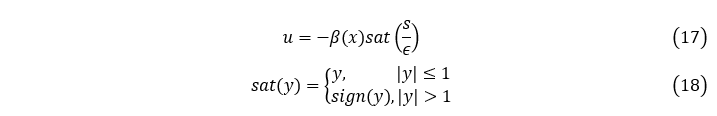
为了提高精度,应选择尽可能小的 ,但是当有时间延迟或者未建模的快速动力学因素时, 太小会引发抖动。
实例