滑模控制思考

滑模控制率设计

针对 MIMO 的系统，介绍如何根据 基本滑模控制简介和示例 提到的滑模控制设计思路建立滑模面，注意如果输入可以解耦的话，可以直接针对每个输入进行单独的设计就可以了

考虑这样的一个系统模型：

$$\begin{array}{l}\dot{x}=f\left(x\right)+g\left(x\right)u\\ y=h\left(x\right)\end{array}$$

定义其滑模面为：

$$s=\sum {\lambda }_i{y}^{\left(i\right)}$$

其中滑模面需要满足 2 个条件：

• 当 s=0 时，有 y→0；如果是跟踪问题 y 替换为 e 就可以
• relative degree = 1

relative degree 的意思是 $\dot{s}$ 中显含 u，因为只有这样我们才可以根据 $\dot{s}$ 的形式推出 u 的表达式，使得滑模变量按照设计的滑模面趋向 0

一种设计滑模面的方法

考虑一个 relative degree = 4 的系统，这意味着在 $y^{(4)}$ 中首次显含 u，因此为了 使得滑模面 s 的 relative degree = 1, s 中必然包含 $y^{(3)}$，或者说 $\text{dddot}y$

对上面系统，考虑这样一个 3 阶的系统：

$$\left[\begin{array}{c}\dot{y}\\ \ddot{y}\\ \text{ddddot}y\end{array}\right]=\left[\begin{array}{ccc}& 1& \\ & & 1\\ & & \end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ \ddot{y}\end{array}\right]+\left[\begin{array}{c}\\ \\ 1\end{array}\right]v$$

先不考虑滑模控制，注意到系统是完全可控的，使用经典的 全状态反馈，有：

$$v=-F\left[\begin{array}{c}y\\ \dot{y}\\ \ddot{y}\end{array}\right]=-\left[\begin{array}{ccc}{F}_1& F_2& F_3\end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ \ddot{y}\end{array}\right]$$

此时闭环系统结构为：

$$\left[\begin{array}{c}\dot{y}\\ \ddot{y}\\ \text{ddddot}y\end{array}\right]=\left[\begin{array}{ccc}& 1& \\ & & 1\\ -F_1& -F_2& -F_3\end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ \ddot{y}\end{array}\right]$$

^eqn-control-structure

事实上这就是配置闭环系统的极点，此时设计 $F_i$ 可以使得闭环系统稳定，从而期望的状态收敛为 0

note

关于状态反馈的实现可以参考四旋翼无人机轨迹控制

上面的设计思路给我们这样的启发，如果只看 ^eqn-control-structure 的最后一行，实际上给我们这样一个系统的等价表达形式：

$$\text{ddddot}y=-F_{1}y-F_2\dot{y}-F_3\ddot{y}$$

而如果取这个为滑模面，就可以保证其收敛，其形式为：

$$s=\text{ddddot}y+F_{1}y+F_2\dot{y}+F_3\ddot{y}$$

^eqn-sliding-mode

note

我个人的想法是，滑模面实际上是一个状态空间中的几何结构。如果采用状态反馈可以实现系统稳定控制，那么这个几何结构就包含了状态空间中的零点。换句话说，存在一条在该滑模面上的光滑曲线使得初始状态作为曲线起点，零点作为终点

^630fc4

remark

如果使用这样的状态反馈来生成滑模面结构，实际上就启发我们可以使用其余的控制方式来生成滑模面，比如PID。

@liuSecondOrderSlidingMode2021好像就是用PID滑模面做的

除了上面的选取方法，还有一种思路是研究系统：

$$\text{ddddot}y+F_{1}y+F_2\dot{y}+F_3\ddot{y}=u$$

然后计算 u 带入控制方程后的系统的稳定性，就是经典控制理论中的传递函数分析

控制量设计

在确定好了滑模面结构后，我们期望将滑膜变量控制在滑模面上，因此可以通过这个 滑模面的约束关系 导出控制量 ^e88787

对 ^eqn-sliding-mode 设计约束关系为：

$$\dot{s}=-k\mathrm{sign}\left(s\right)$$

如果按照这个约束方程，可以通过 李雅普诺夫稳定性 来证明滑模变量是大范围渐进稳定的

因此有：

$$\begin{array}{l}\dot{s}=\text{ddddot}y+F_1\dot{y}+F_2\ddot{y}+F_3\text{ddddot}y\\ \dot{s}=\bar{f}\left(x\right)+\bar{g}\left(x\right)u+F_1\dot{y}+F_2\ddot{y}+F_3\text{ddddot}y\\ \dot{s}=-k\mathrm{sign}\left(s\right)\end{array}$$

^eqn-control-law

从而可以得到：

$$u=\frac{1}{\bar{g}\left(x\right)}\left(-\bar{f}\left(x\right)-\left(F_1\dot{y}+F_2\ddot{y}+F_3\text{ddddot}y\right)-k\mathrm{sign}\left(s\right)\right)$$

根据上式，为了计算控制向量，我们需要系统的全状态 x 以及输出的各阶导数，这意味着需要 观测器 + 求导，会引入很多误差

误差分析

为了考虑观测误差、传感器误差、计算误差带来的影响，将 ^eqn-control-law 改写为：

$$\begin{array}{l}\dot{s}=\left(a+\Delta a\right)+\left(b+\Delta b\right)u\\ u=\frac{1}{b}\left(-a-k\mathrm{sign}\left(s+\Delta s\right)\right)\end{array}$$

^eqn-sliding-mode-with-error

其中 a, b 是观测、测量、计算出的值 (将其汇总)，s 代表真值，$s+\Delta s$ 代表我们实际使用的 s 的值，$\Delta a,\Delta b,\Delta s$ 代表用于计算控制输入的值和对应真值的差

可以根据上面的示意式子推得：

$$\dot{s}=\left(\Delta a-\frac{\Delta b}{b}a\right)+\left(1+\frac{\Delta b}{b}\right)\left(-k\mathrm{sign}\left(s+\Delta s\right)\right)$$

^eqn-ds-with-error

可以搭建一个 滑模变量收敛 的示意模型，展示 s 收敛的情况：

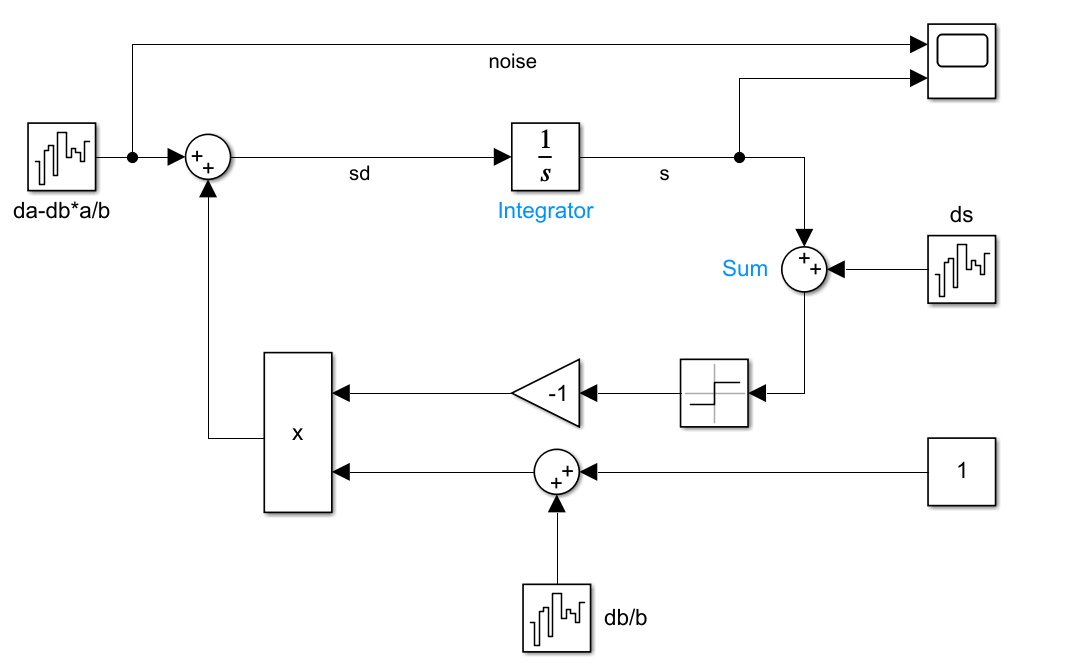
其中 band width white noise 的 noise power 设置为 0.01，s 初始值为 5

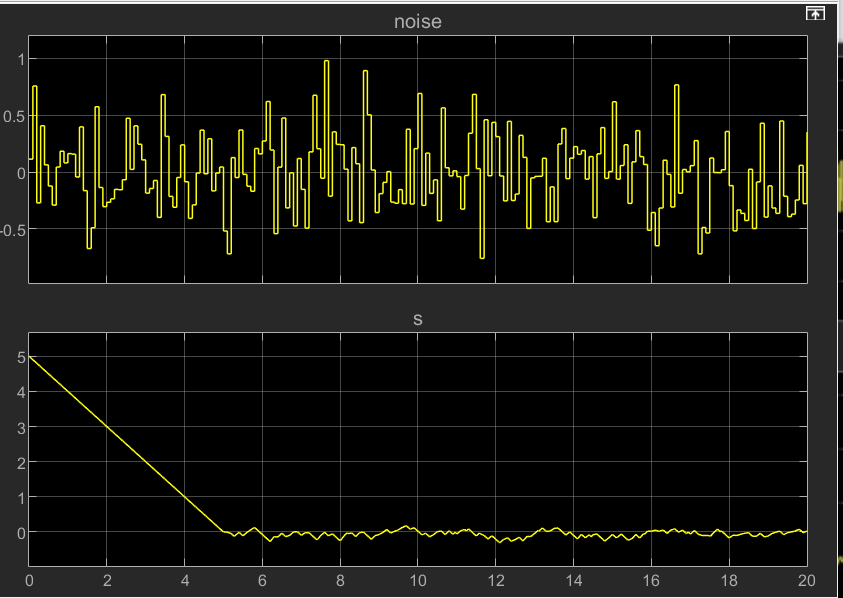
可以发现，在设计的反馈结构下，其滑膜变量在未知干扰下还是可以快速收敛

什么事滑模控制的有限时间收敛

微分方程解释

知乎上 ^[1] 给了从微分方程角度的解释，摘录如下：

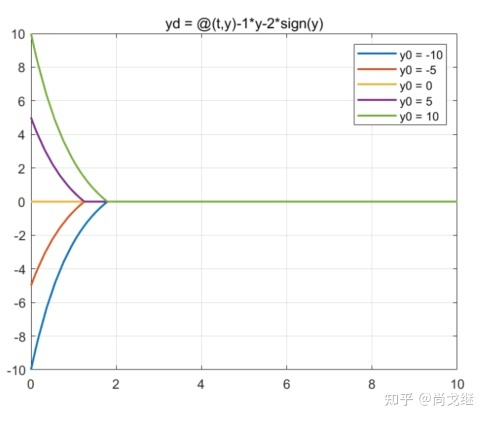
考虑这样一个微分方程：

$$y^{\prime }+y=0$$

其解析解为：

$$y=e^{-t+c_1}$$

不同初值情况下 $y$ 的变化情况如下：

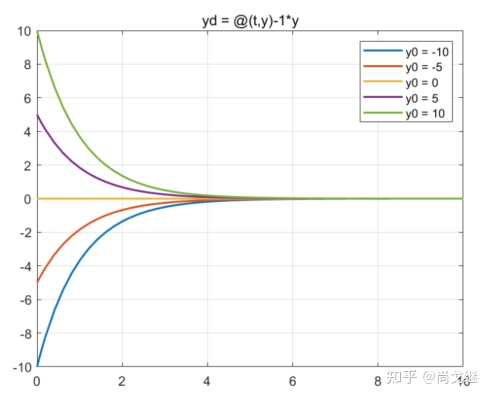
但是可以发现，这个情况 并不是有限时间收敛的指数收敛/渐进收敛，因为永远得不到严格的 $y=0$

但是如果考虑：

$y^{\prime }+y=-2$

此时系统可以表示成一个一节系统的传递函数：

$\frac{Y(s)}{U(s)}=\frac{1}{1+s}withu(t)=-2$

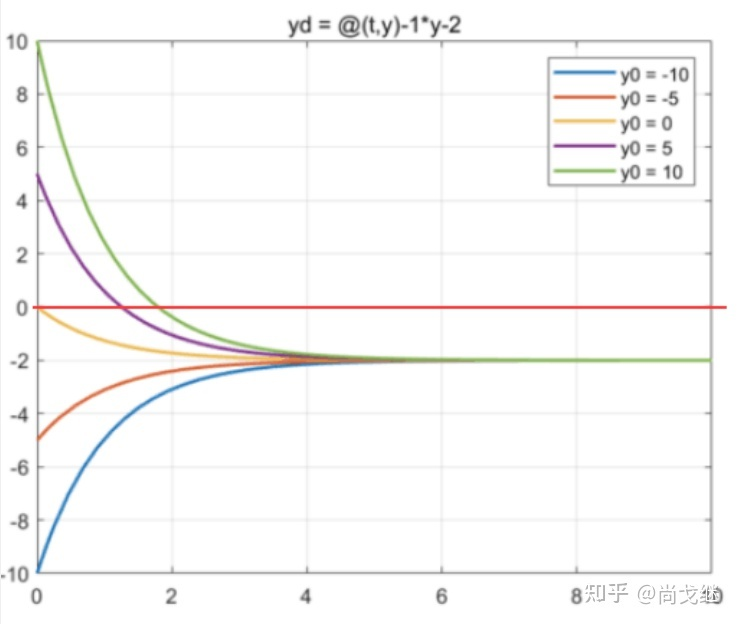
这种情况下虽然依旧是指数收敛，但是如果以收敛为 0 为目标，可以看到最上面的两种初始情况都能保证在有限时间内有 y=0 ，但同时，引入这个常数偏置项的后果是，最终收敛的值并不是 0。

考虑这样一个系统：

$$y^{\prime }+y=-2\mathrm{sign}(y)$$

这样的系统就是有限时间收敛

---

有了上面的基础我们可以开始讨论滑模控制的有限时间收敛了

滑模控制具有 2 个阶段：

• 系统收敛到滑模面：$s\to 0$
• 系统在滑模面上收敛至原点：$y\to 0$

滑模控制的有限时间收敛，主要是让第一个过程有限时间收敛，因为两者是先后发生的，如果两个过程都是渐进收敛，那么系统 整体的收敛到有界的时间 就不好计算，但是如果第一个过程有限时间收敛，第二个过程有限时间有界收敛，那么整体的收敛到有界的时间也就比较好算，系统性能有保证。

当然也可以让第一个和第二个过程都有限时间收敛，但个人认为意义不大。因为现实中不可能存在真的收敛为 0。只需要研究对应的滑模面，通过设计常数保证有界收敛足够快就可以。

比如：

$$y^{\prime \prime }=-2y^{\prime }-y$$

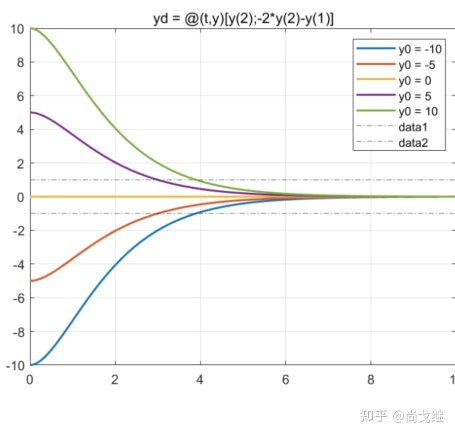
而 $y^{\prime \prime }=-y^{\prime }-2y$

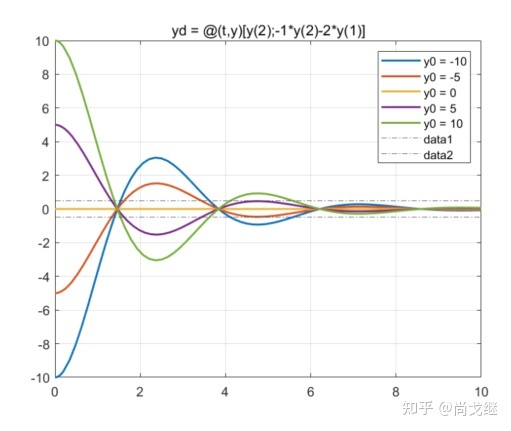
通过设计滑模面的参数，可以控制到达滑模面之后的系统表现：抖动、速度、稳态值。

实现方法

使用 李雅普诺夫稳定性 方法，构造并证明其方法

考虑滑模面动态满足： ^eqn-sliding-mode-with-error

推导得到： ^eqn-ds-with-error

构造李雅普诺夫函数：

$$\begin{array}{l}V=s^2\\ \dot{V}=s\dot{s}=s\left[\left(\Delta a-\frac{\Delta b}{b}a\right)+\left(1+\frac{\Delta b}{b}\right)\left(-k\mathrm{sign}\left(s+\Delta s\right)\right)\right]\end{array}$$

参考 定义，为了使得有限时间收敛，构造条件：

$$\dot{V}=s\dot{s}<-ϵs$$

从而需要有：

$$\left(\Delta a-\frac{\Delta b}{b}a\right)+\left(1+\frac{\Delta b}{b}\right)\left(-k\mathrm{sign}\left(s+\Delta s\right)\right)<-ϵ$$

最终控制参数 $k$ 需要满足：

$$\begin{array}{l}k>\frac{\alpha +ϵ}{\beta }\\ \alpha =\left(\Delta a-\frac{\Delta b}{b}a\right)\\ \beta =\left(1+\frac{\Delta b}{b}\right)\end{array}$$

实验参考代码：

%研究不同的滑模面设计s(x)和不同的滑模面初值s(x(t_0)) 对x的影响
clear all
close all
clf

tspan = [0 10];
num_line = 5;
initial_value_range = 10;
y0list = linspace(-initial_value_range,initial_value_range,num_line);


% example 1 : y' = - y
% fun = @(t,y) -2*sign(y) ;
% order = 1;
% 
% % example 2 : y'' = -2y' - y  => (y)' = (y') & (y')' = -2(y') - (y) 
fun = @(t,y) [y(2);-1*y(2)-2*y(1)];
order = 2;

% example 3 : y'' = -y' - 2y  
% fun = @(t,y) [y(2);-y(2)-2*y(1)];
% order = 2;

for i = 1:1:num_line
    
    %这里对于高阶的系统，只有0阶导有初值，高阶导皆为0
    %如果需要测试高阶导也有初值的情况，更改下面y0的表达式
    y0 = y0list(i)*[1,zeros(order-1,1)];
    [t,y] = ode45(fun, tspan, y0);
    plot(t,y(:,1),'linewidth',1.5,'DisplayName',['y0 = ',num2str(y0list(i))])
    hold on
    
end

title(['yd = ',func2str(fun)])
yline(-.5,'-.')
yline(.5,'-.')
legend
grid on

离散时间滑模控制的时延问题

问题构造

考虑这么一个系统，这里用的是高阶的滑膜，但其实先不考虑滑膜的问题，只把它当一个普通的系统来看，这里主要说明的问题也与高阶滑模控制无关。

$$\begin{array}{c}{\dot{z}}_1=z_2,{\dot{z}}_2=u\\ u\left(z_1\right)=-K\mathrm{sign}\left(z_1\right)\\ K>0\end{array}$$

如果不考虑采样时间，这个系统的相轨线如下图是一个稳定的闭合曲线：

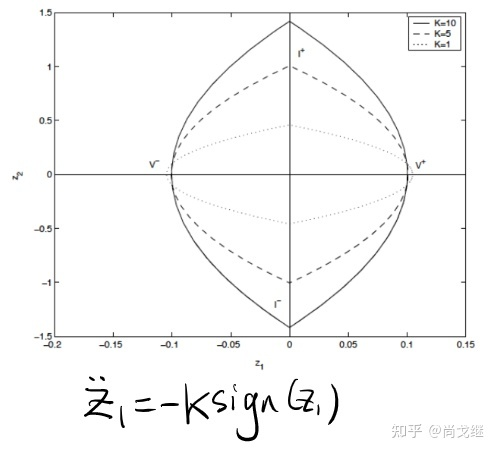
如果系统如下式子：

$$\begin{array}{c}{\dot{z}}_1=z_2,{\dot{z}}_2=a\left(\cdot \right)+b\left(\cdot \right)\cdot u\left(z_1\right)\\ u\left(z_1\right)=-K\mathrm{sign}\left(z_1\right)\\ 0<b_m<b\left(x\right)<b_M\left|a\left(x,t\right)\right|⩽a_M\end{array}$$

此时系统稳定的条件是

$$K>\frac{a_M}{b_M}$$

同样不考虑采样时间，系统的相轨线为：

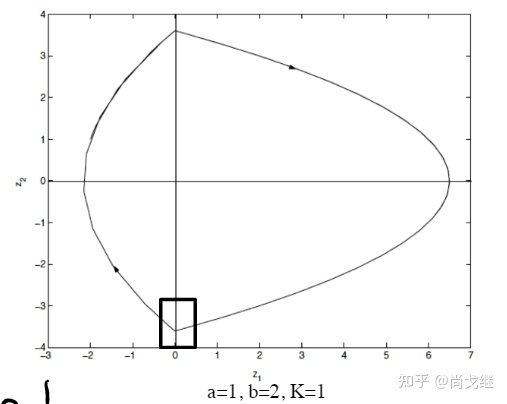
但是如果考虑了采样时间之后，系统的真实相轨线为：

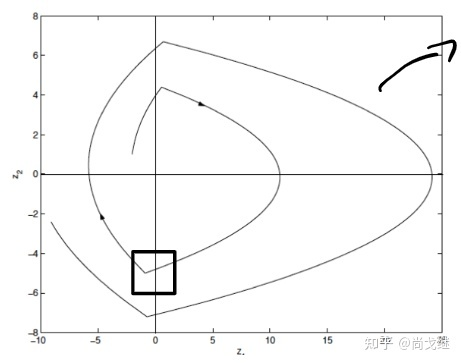
因为在 z1 变号之后的下一个时刻，负责计算控制信号的处理器还不知道 z1 变号，所以 sign(-) 还是用的之前的符号，这就导致一个时延，也即图中方框里的内容，结果是系统发散了，这很明显不是我们想要的。

解决方法

有一个非常简单粗暴但实用的方法

写得很复杂，原理一句话就能说清楚：

在”处理器“（或者说计算单元）察觉到 z1 变号之后的计算下一个 u 的时候，把 k 增大。注意只在这一步增大，没有变号的时候就用正常的 k。

结合图来解释这个原理：

• 考虑采样时间，且全程不改变 k 值，那么就是 A->B->D->....系统逐渐发散
• 考虑采样时间，且使用这里上面提出的方法：在 B 点，处理器察觉到 z1 变号了，把 K 增大，把相轨线“扭”过去，这样能保证系统依旧稳定。

如果仿真地久一点

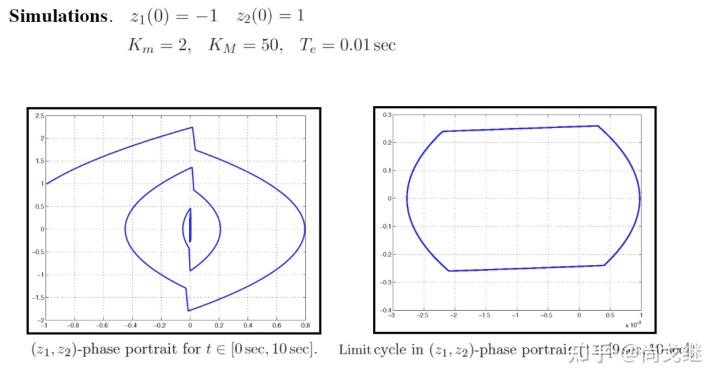可见这个离散时间系统保持稳定，逐渐收敛到有界，z1 和 z2 都在 0.001 以内波动。

参考

引文

• 滑模控制的一些思考-滑模面设计和进阶滑模控制 - 知乎
• 滑模控制的一些思考-有限时间收敛和离散滑模控制的时延问题 - 知乎

脚注

---

1. 滑模控制的一些思考-有限时间收敛和离散滑模控制的时延问题 - 知乎 ↩︎