Chap3 根轨迹分析
Chap3 根轨迹分析
根的作用
所谓根就是极点,我们知道极点在复平面上的位置会很影响系统的时域响应,可以参考系统的响应。我们分析了一阶、二阶系统的系统响应特性,而注意到,代数基本定理告诉我们高阶系统也就是多个一阶、二阶系统的叠加,因此我们需要研究的所有线性时不变系统实际上都可以归类到对一、二阶系统中,而根对一、二阶系统的时域响应起了决定性作用
既然根如此重要,我们自然地可以想到,通过在系统前添加补偿器来调节根的位置,这就可以得到我们想要的系统特性,这就是研究根轨迹的出发点
根轨迹变化规律
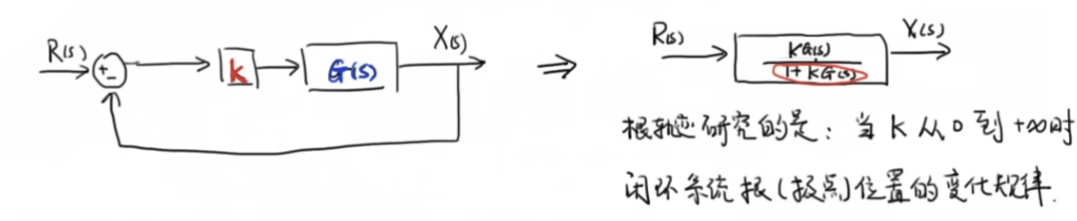
对一个闭环系统,其闭环传递函数可以表示为:
我们研究的是 从 到 变化时,系统 极点在复平面上的变化规律
如果反馈也带了一项传递函数,那么分析对象就变为了
note
我们通过根轨迹,分析的系统是开环系统的响应,也就是对控制对象的分析
考虑极点:,设:
其中 被称为零点,用⭕来表示,开环系统有m个零点,为m阶; 为极点,用❌来表示,有n个极点,为n阶
规则1:根轨迹数量
theorem
如果n>m,那么有n条根轨迹;如果m>n,共有m条根轨迹
也就是说,具有零极点阶数最大的数目的根轨迹
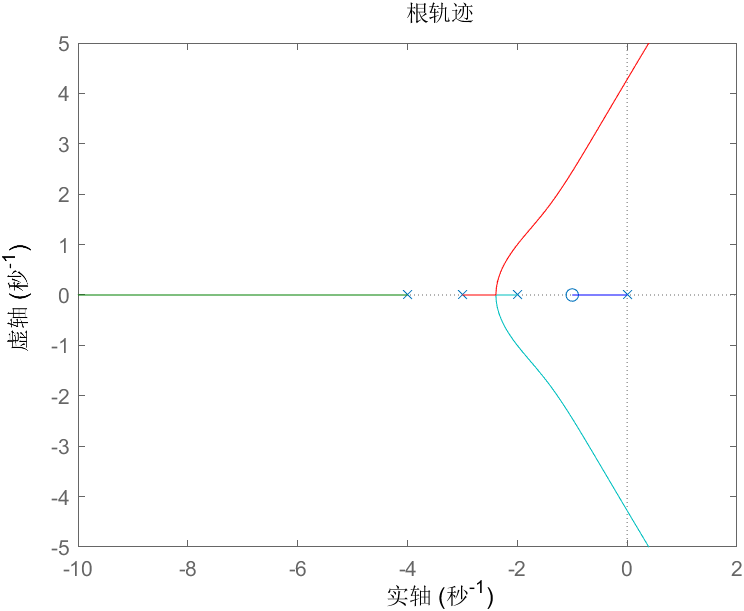
比如系统 ,其根轨迹如下图
规则2:极点向零点移动
theorem
当n=m时,随着k从0到 ,根轨迹从G (s) 的极点向零点移动
这从系统极点表达式可以直接看出
规则3:实轴上根轨迹存在于奇数点左边
theorem
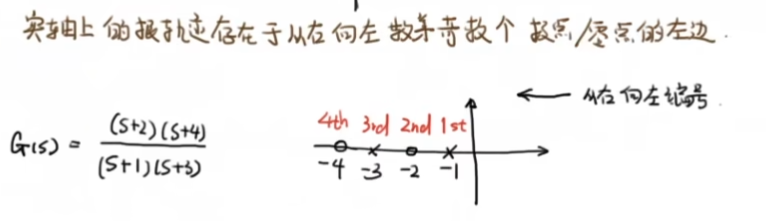
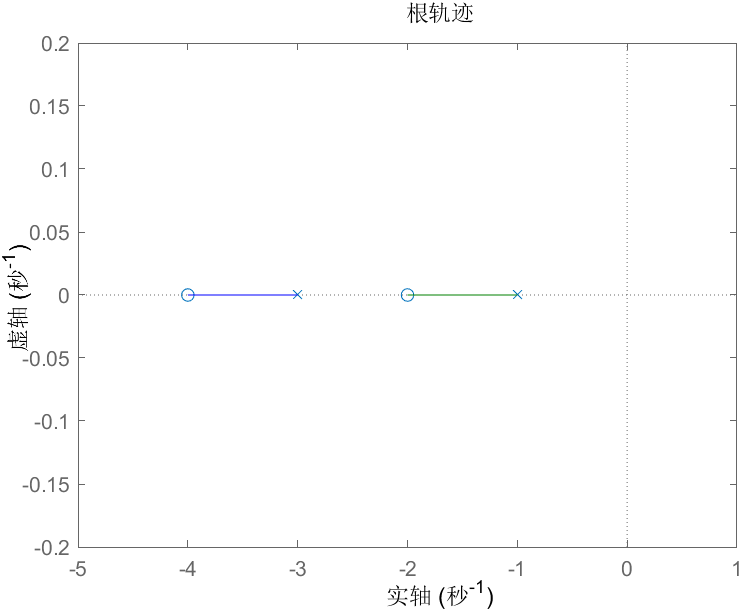
note
仅仅在实轴上有这个规则
规则4:复数根轨迹通过实轴对称
theorem
如果复数根存在,那么一定是共轭的,这表明其根轨迹通过实轴对称
规则5:若n>m,那么有n-m个极点指向无穷;反之亦然
theorem

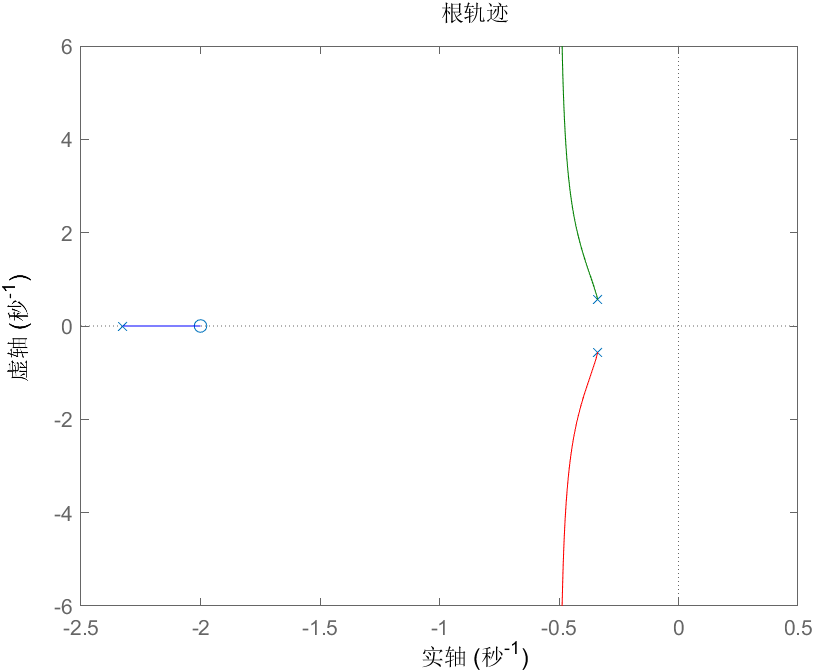
比如系统:,根轨迹为: 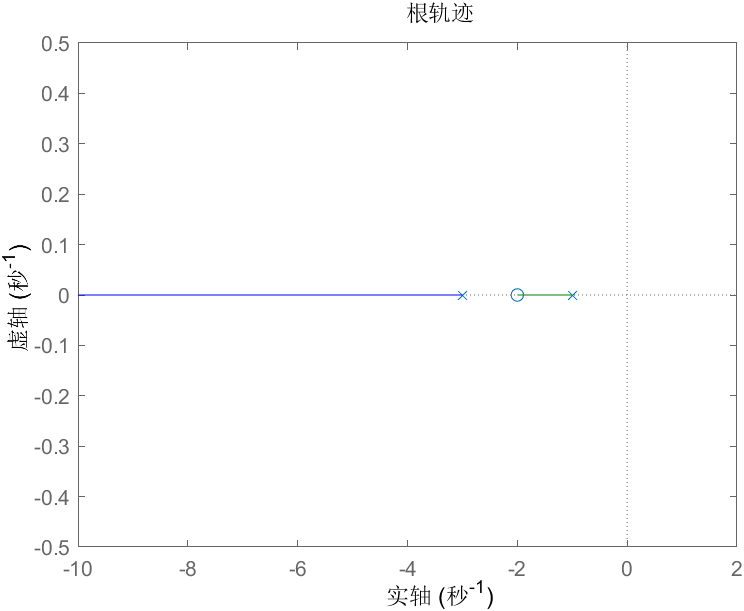 反过来,
反过来,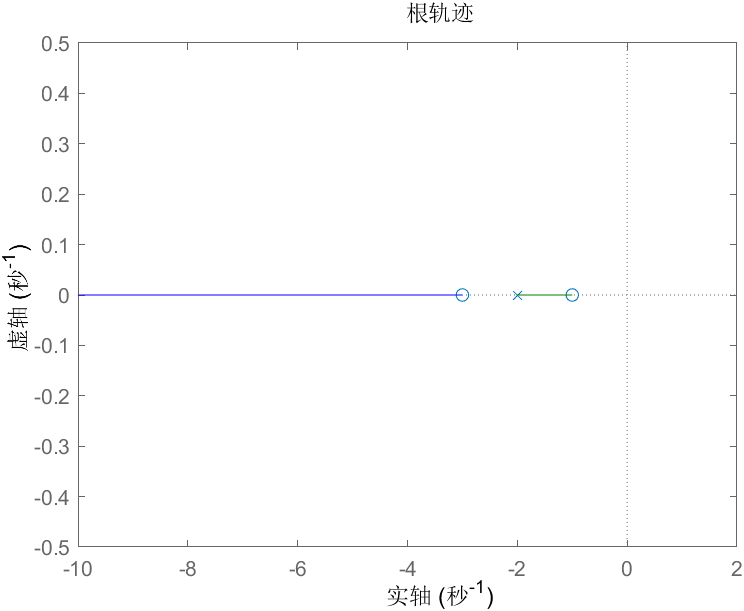
规则6:根轨迹沿着渐近线移动
根轨迹沿着渐近线移动:
- 渐近线和实轴的交点 ,其中p是极点,z是零点
- 渐近线和实轴的夹角
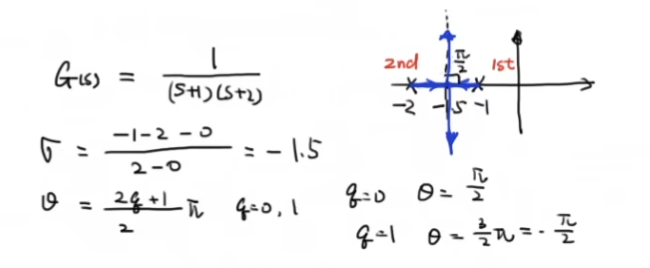
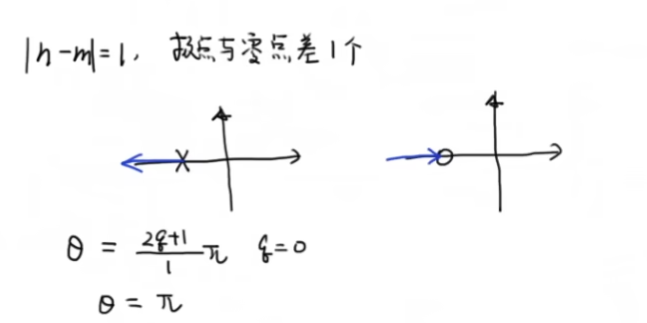
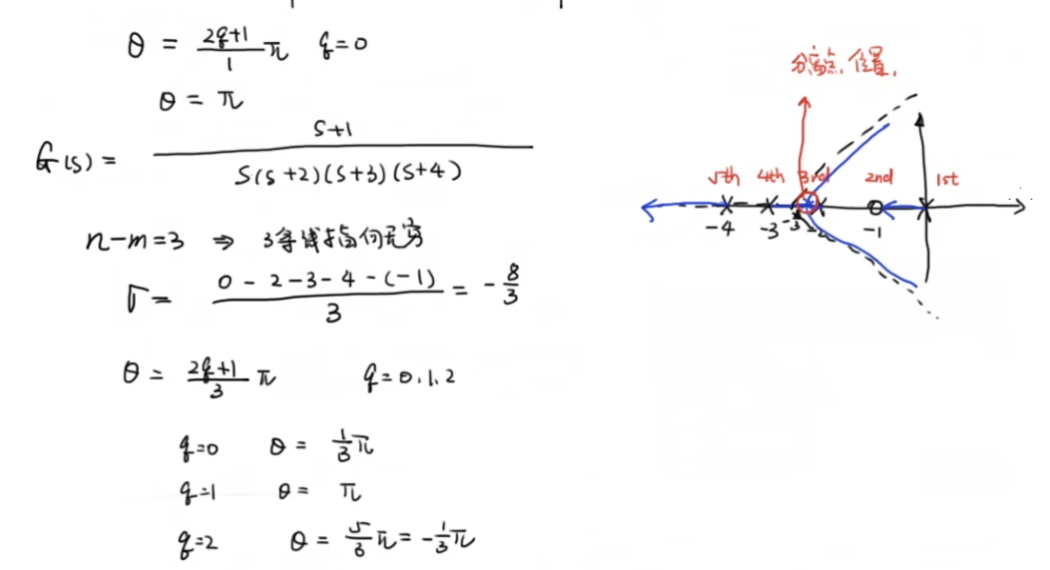
上面系统的根轨迹为:
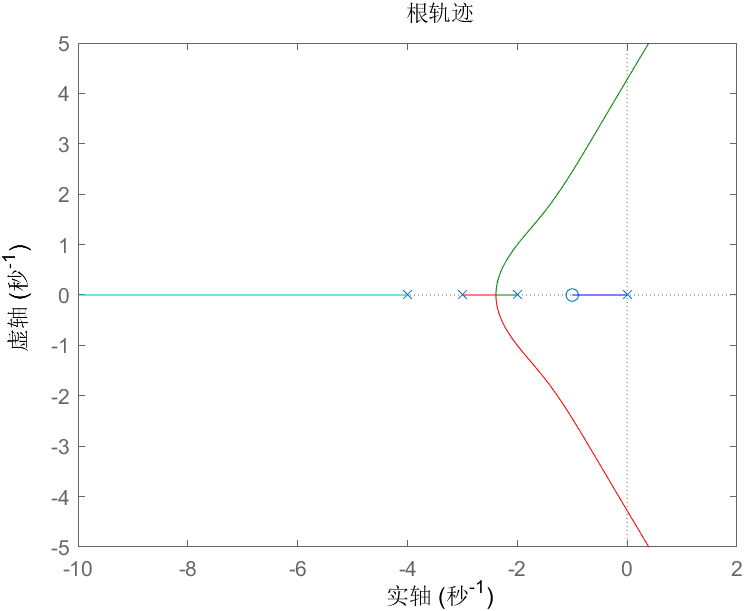
problem
出现一个奇怪的问题:matlab 仿真结果出现了相反的结果,明明是同一个系统?
z = [-1];
p = [0 -2 -3 -4];
k = 1;
sys1 = zpk(z, p, k)
rlocus(sys1)
q = 0:(abs(length(p)-length(z))-1);
theta = rad2deg((2.*q + 1)./ abs(length(p)-length(z)).* pi)
sys2 = tf([1 1], [1 9 26 24 0])
rlocus(sys2)
q = 0:(abs(length(p)-length(z))-1);
theta = rad2deg((2.*q + 1)./ abs(length(p)-length(z)).* pi)
仿真结果分别为:
根走向了不同的虚轴,这意味着相差了180°相位?
但是两个系统是一样的:

如果减少根中的-4的极点,两者就一样了…
note
不过起始也无所谓,反正根轨迹的意义是在给定K之后极点的位置,那么实际上差180度相位代表着极点共轭,两个是对称的,对系统结果分析应该没有什么影响
根轨迹的性质
根轨迹的应用案例
我们首先给一个根轨迹的应用例子,考虑下面这样一个2阶系统:
我们期望使用根轨迹的方法来设计 从而控制响应结果,那么将其化为框图:
和 相关的项为原始系统的分子,那么有:
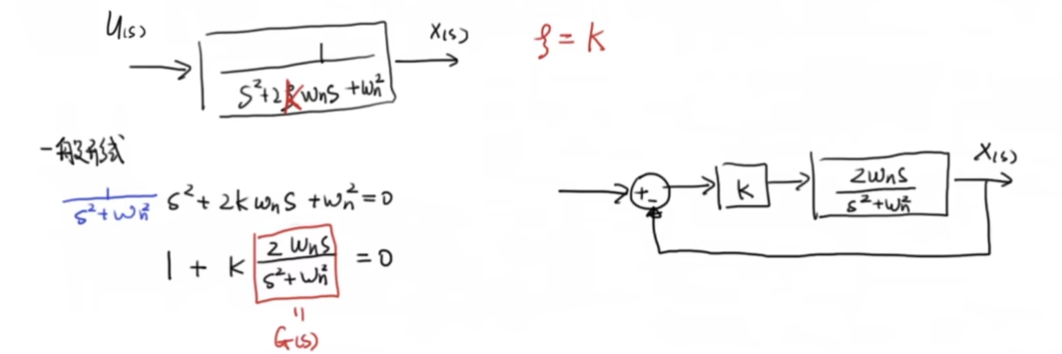
对系统 而言,其具有2个虚轴上共轭的极点和一个原点出的零点
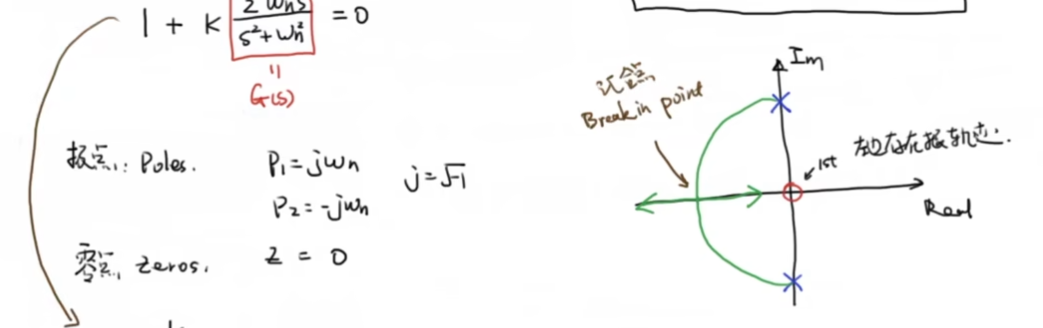
我们来计算这个汇合点:
这也意味着汇合点在k=1时达到,有下面的分析结果,其和我们对二阶系统的分析结果一样
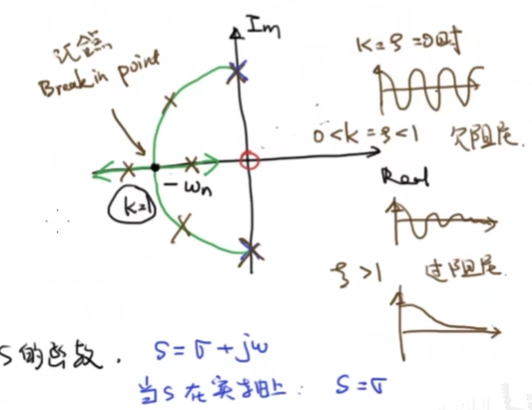
根轨迹的几何性质
注意到复数可以表示为幅角形式,那么对一个复数 ,将其带入系统 中后,得到的结果有:
- 幅值为复数 到零点向量的幅值之积÷ 到极点向量的幅值之积
- 相位为复数 到零点向量的相角之和- 到极点向量的相角之和
举例而言:,我们期望求 的结果:

现在回头观察我们的根轨迹的基本形式,有:
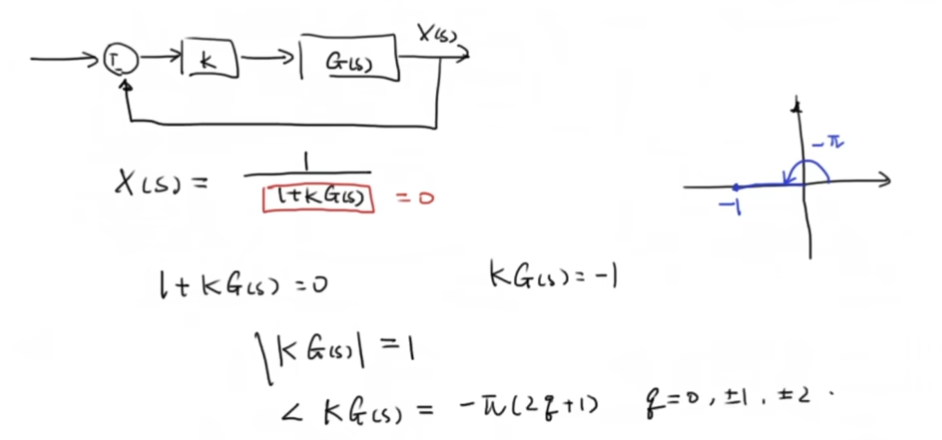
通过上面的几何角度的理解,我们可以通过调节根的位置得到新的控制器——超前补偿器 (Lead Compensator)
超前补偿器
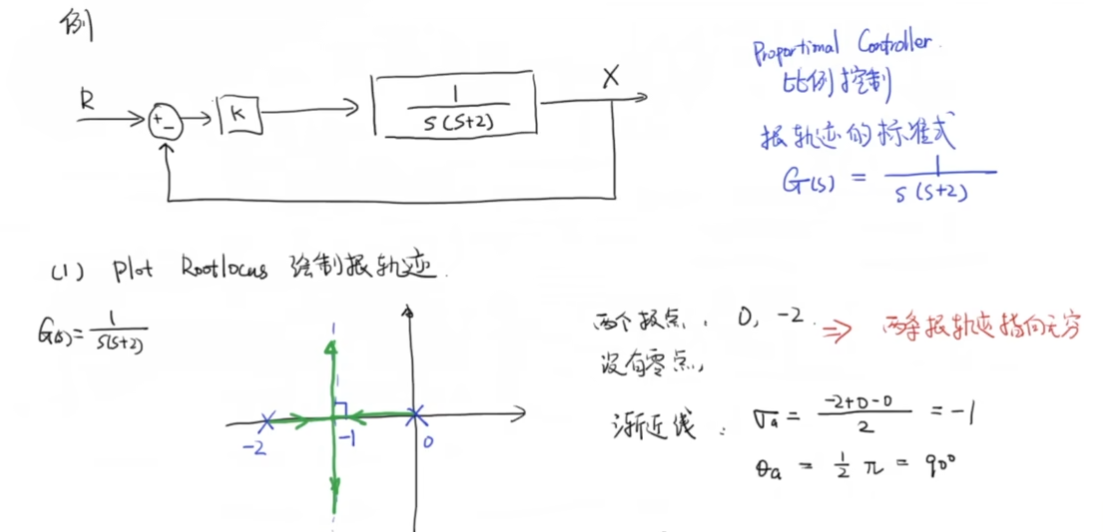
我们对这个系统的性能进行分析,考虑输入一个单位冲激 :
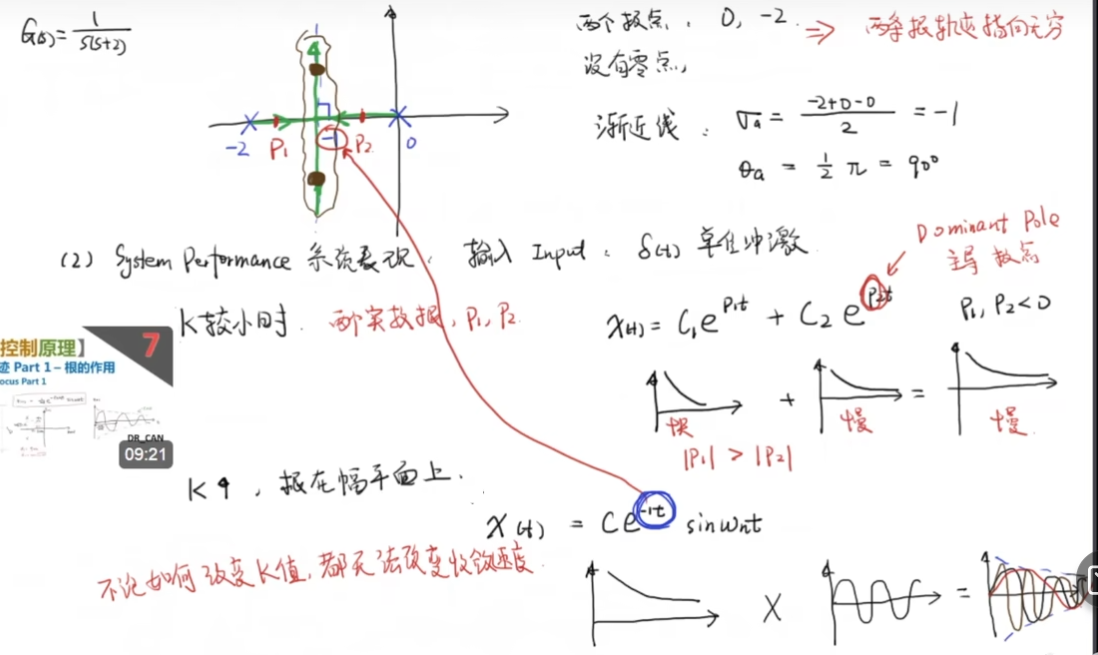
如果我们期望系统能够加快其收敛速度,那么我们需要调节根轨迹:
譬如说我们期望根在 处,那么:
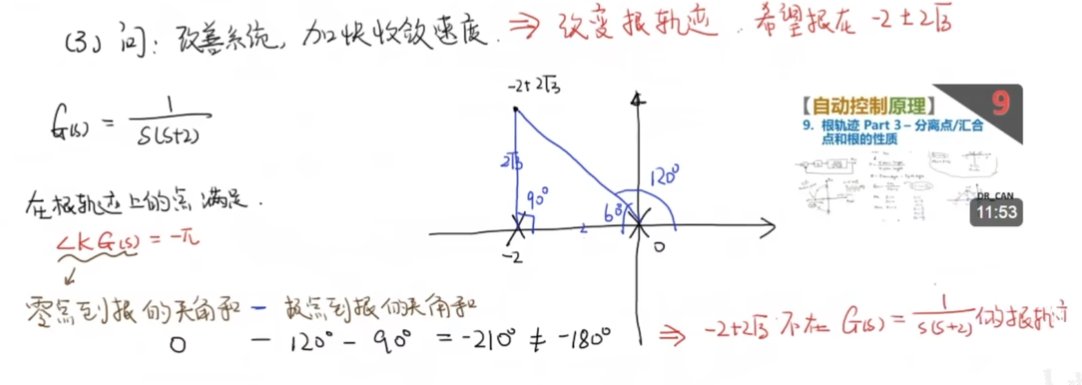
这表明这个期望根不在目前的根轨迹上,我们需要弥补这样的轨迹。一个简单的思路是:
我们增加一个30°的零点,从而满足了相角限制
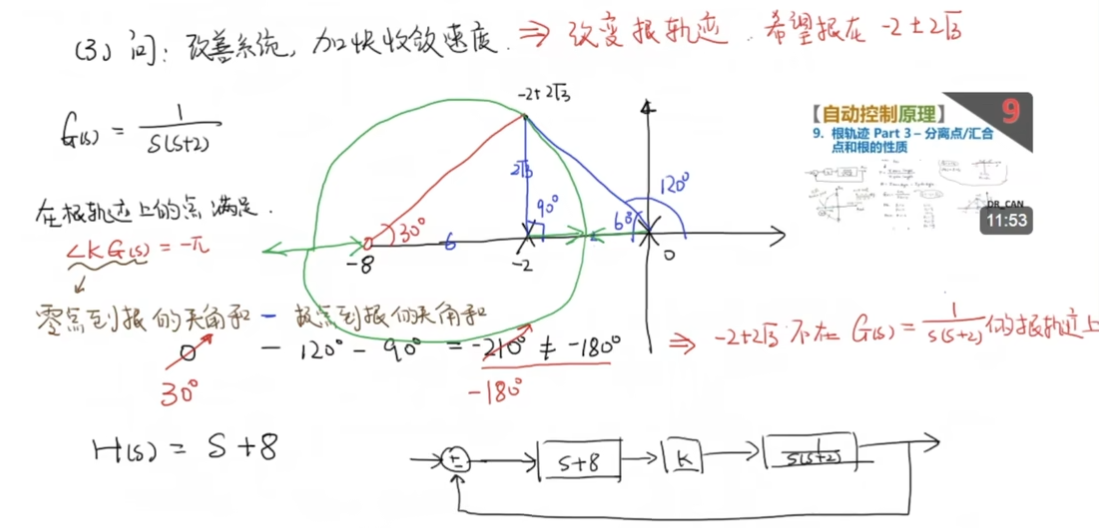
这就变成了一个PD控制,一般来说实际控制中我们尽量不期望这样的控制:
- 被动原件无法实现这样的控制 (微分项) #todo
- 对高频噪声敏感,通过伯德图显然可以看出
为了避免这样的问题,就引出了我们对超前补偿器,其形式为:
即引入零点的同时也引入极点,其中
其思路是:将期望的30°拆分为2部分:40°-10°,即一个40度的零点和10度的极点
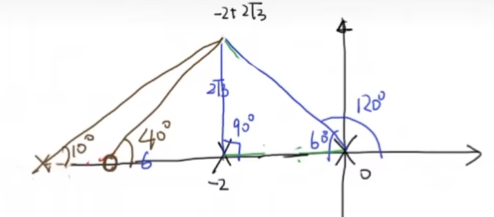
我们可以计算加入了超前补偿器后的根轨迹,其汇聚点为:
注意到 ,这意味着将原来的-1位置的渐近线向左边拉,根轨迹向左,提高稳定性,加快反应速度
观察其伯德图,形式为:
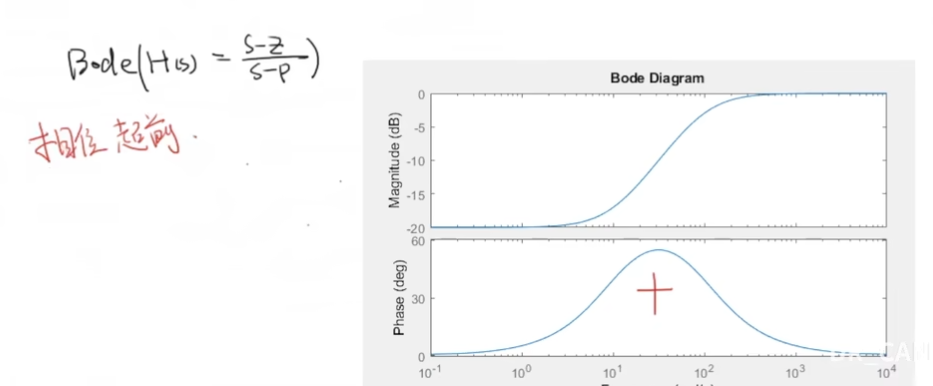
注意到其在一部分频率处提前了相位,这也是其为什么叫超前补偿器
滞后补偿器
前面的 超前补偿器 考虑的是对系统进行极点配置的控制器,其影响的是系统的动态响应特性;我们换个角度,从系统时域上的稳态误差入手,来看看有没有办法能够削减稳态误差?
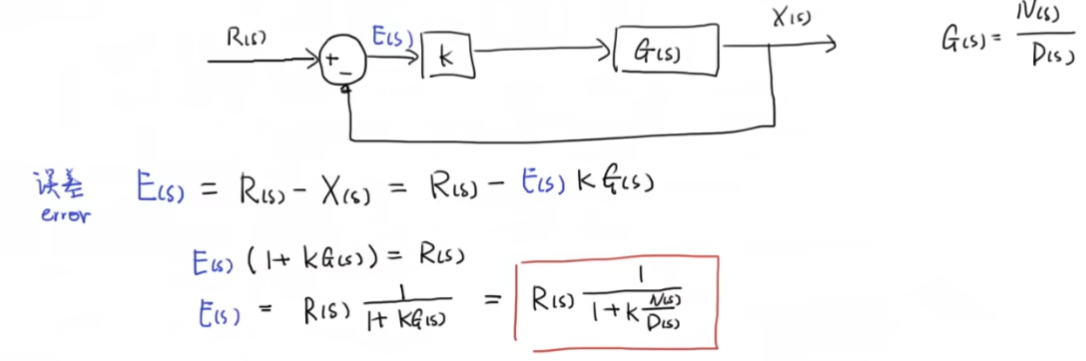
考虑输入 为一个单位阶跃,那么稳态误差可以使用 终值定理和稳态误差进行计算:
如果引入补偿器 ,即:
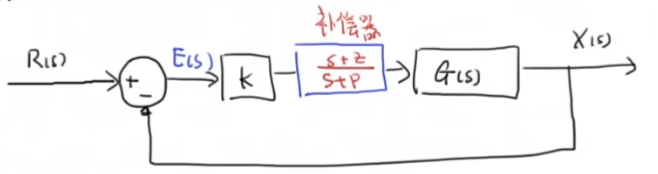
那么稳态误差:

如果 ,那么此时 ,这意味着稳态误差为0,补偿器形式上为:
是一个PI控制
设计案例
对系统:
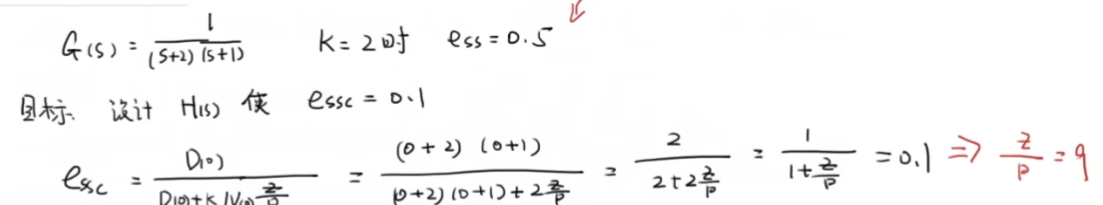
通过给定稳态误差上限,我们可以得到 的比例,并不能确定完整的值。我们可以给一些例子值仿真看看结果形式:
| p | z | 结果 |
|---|---|---|
| 0.1 | 0.9 | 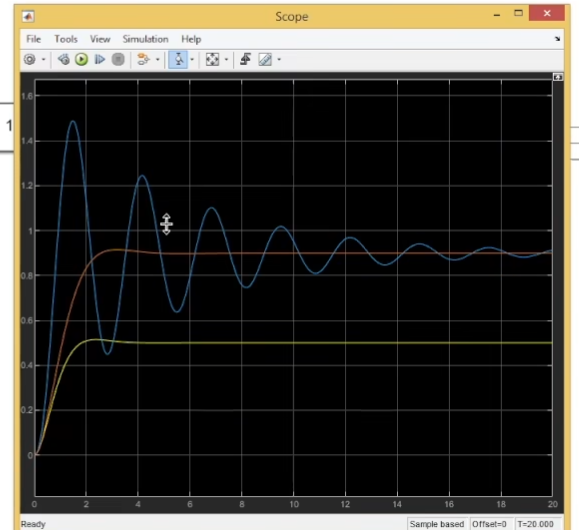 |
| 1 | 9 | 同上 |
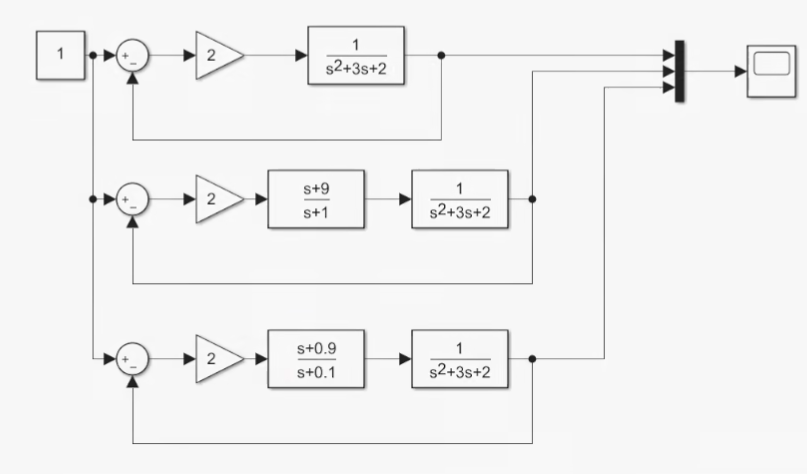
其中黄线是没有补偿器的情况,对应第一行模型;蓝线代表极点-1的情况,红线代表极点-0.1的情况
这可以从根轨迹的角度来看:
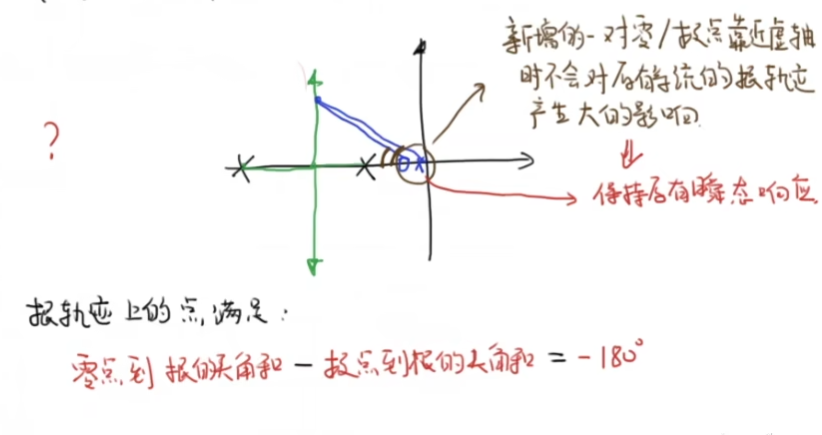
这也确实是,黄线和红线的瞬态响应是很相似的,也就是说我们希望能够尽量的保证滞后补偿器的零极点贴近虚轴,这样相角差距不会太大,系统根轨迹变化不会很大