Chap2 稳定性分析

问题引入

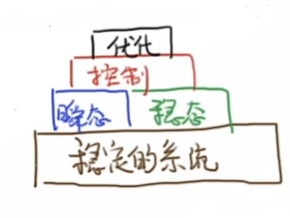
系统的稳定性是第一位的

稳定性例子

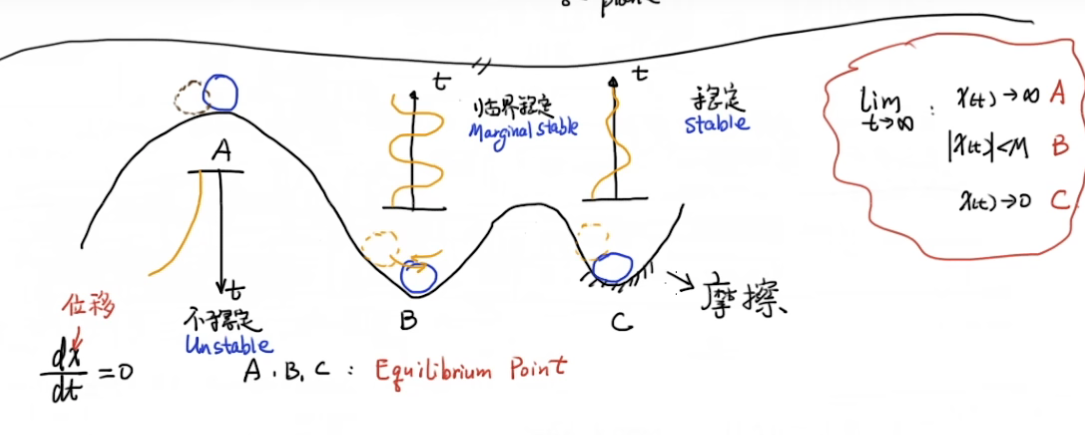
更进一步，我们考虑将小球化为一个系统，对B小球而言，如果给定其一个有界输入，那么可以期盼，其输出也是一个有界的，我们将这种系统称为：BIBO稳定

数学分析

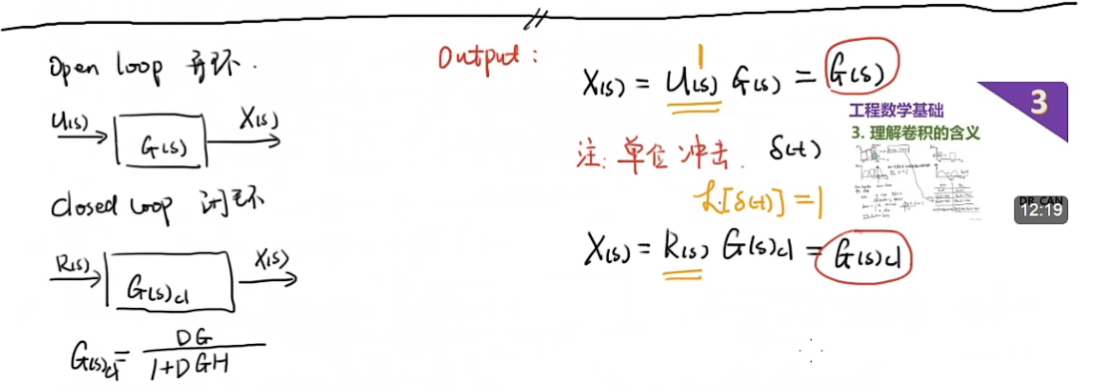
我们一般通过给定单位冲击来研究系统的稳定性（这就够了）

为了研究一个系统的稳定性,，我们首先考虑一个特殊情况的响应 (对 $\delta$ 的响应) ：

考虑系统 $G(s)=\frac{1}{s^2+s-6}=\frac{1}{(s+3)(s-2)}$，其单位冲击响应为：

$$\begin{array}{rl}X(s)& =1\cdot G(s)=\frac{c_1}{s+3}+\frac{c_2}{s-2}\\ x(t)& ={\mathcal{L}}^{-1}[X(s)]=c_1{e}^{-3t}+c_2{e}^{2t}\end{array}$$

这表明系统并不稳定

remark

上面说系统的稳定性研究，实际上是基于极点的某种不变性的，也就是说一般来讲你给定一个输入，其不影响输出中的函数成分，只会影响成分之间的比例关系在；也就是说输出的函数性质是由系统本身决定的，稳不稳定也就只需要看系统的传递函数就可以了

利用复数上的代数基本定理，我们可以得到：

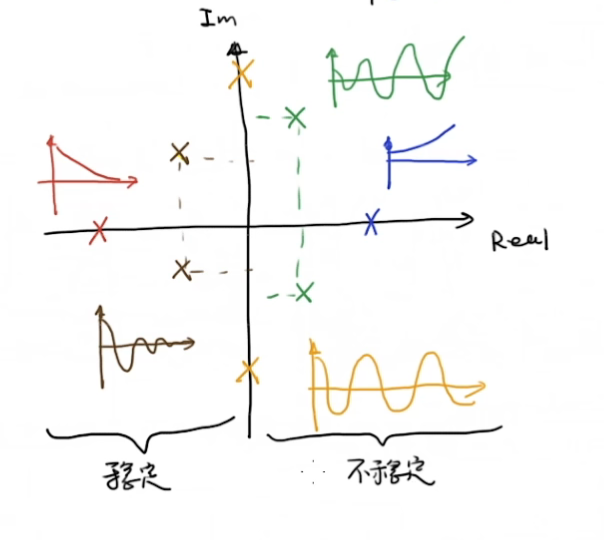
又由于线性系统的可加性，我们可以说明：

corollary

极点在左半平面系统稳定

终值定理和稳态误差

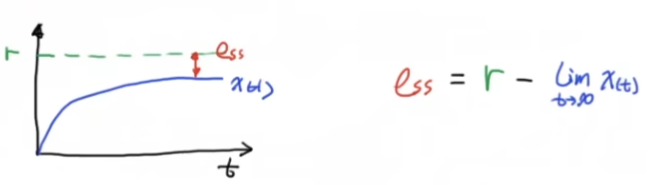
我们知道如果系统只是稳定的，并不能说明系统能够达到想要的reference位置，其中一个表征量是稳态误差，我们期望对常值输入的这种系统，可以有系统稳定后的稳态误差越接近0越好

为了分析稳态误差，我们有好用的终值定理：

终值定理

$$\underset{t\to \infty }{\lim }x(t)=\underset{s\to 0}{\lim }sX(s),X(s)=\mathcal{L}[x(t)]$$

其适用性具有条件：

当${\lim }_{t\to \infty }x(t)$存在的时候，才可以适用FVT，这也意味着极点都在复平面的左半边

参考

引文

脚注