单索并联机构动力学模型

定义

介绍 单索并联机构 的动力学模型构建，给出其基本的动力学建模技巧

方案

索机构动力学模型是进行索机构原型测试的必要条件，之前研究的运动学模型是动力学模型上的自然延伸，在研究过程中涉及到的主要映射如下：

p246r54

正逆动力学的基本框架如下图：

p250r54

动力学模型介绍

绳索的动力学特性与其长度、材料乃至预紧力都有关系，下面总结了可能影响绳索动力学特性的原因：

• 弹性变形：对长距离绳索以及大负载绳索影响大
• 热变形
• 蠕变 (Creeping？)：是绳索材料中变形的一种特殊形式，比如高分子材料。Creeping 是一种 hysteresis(迟滞) 效应，可以引起绳索一定时间的可恢复拉伸变形
• 下垂 (Saggingg)：由于绳索重力导致的静态变形
• 横向振动 (Transversal vibration)：绳索像琴弦一样的横向振动，会导致 effective length $l_{\mathrm{eff},i}$ 和 tension $f_i$ 出现高频的震动。这一现象在以高加速度运动、绳索质量相对运动平台的质量不可忽略的时候容易出现
• 纵向振动 (Longitudinal vibration)：对大尺度的绳索机器人，绳索材料中的音速导致不可忽略的延迟，从而减小了机器人的动力学带宽 (dynamic bandwidth)；这也出现在超级高加速度运行的机构中
• 并不是完全的可变形的 (Imperfect flexiblity)：绳索通常来说是忽略了其 bending 和 torsional 的刚度的，但在有些情况下，比如金属制造的绳索在小滑轮上会体现出一定的弯曲刚度

动力学模型分析

理想模型

Pott_2018_Cable-Driven Parallel Robots

理想模型中，绳索的传递函数就是一个符号函数，使得拉力为正时传递力，为负时不传递力

这一方法虽然之间实现简单，但是其使得仿真分析变得比较困难，因为这一模型是一个不连续的模型，而且具有强烈的非线性性

弹簧 - 阻尼模型

绳索也被建模为一个并联的弹簧 - 阻尼模型，其中弹簧弹性系数和阻尼比都是可变的，取决于绳索的有效变形长度 $l_{\mathrm{eff},i}$

这一模型忽略了绳索自身的质量，认为绳索的张力只取决于其弹性变形，这表示纵向和横向的振动都被忽略

在此基础上建立绳索的模型为：

p257r57

其中有效绳长的初始条件 $l_{\mathrm{eff},0,i}=l_{N,i}({\mathbf{y}}_0)$ 可以通过绳索原长计算：

$$l_{N,i}(\mathbf{y})=\Vert {\mathbf{l}}_{\mathbf{i}}(\mathbf{y}){\Vert }_2+l_{R,i}(\mathbf{y})+l_{G,i}$$

其中 $l_{R,i}$ 是绳索在滑轮上的长度，$l_{G,i}$ 是绳索在 winch 上的长度。注意到缠绕的绳索长度为 $l_{D,i}=r_i{\theta }_i$，从而可以将有效长度表示为：$l_{\mathrm{eff},i}=l_{\mathrm{eff},0,i}+l_{D,i}$，从而可以计算出变形量为：

p257r48

$$\Delta l_i\left(\mathbf{y},{\theta }_i\right)=l_{\mathrm{N},i}(\mathbf{y})-l_{\mathrm{N},i}\left({\mathbf{y}}_0\right)-l_{\mathrm{D},i}$$

估计模型中弹簧的刚度还是一个未定的问题，目前一般使用弹性模量进行估算：

$$c_i=\frac{E_c{A}_c}{l_{i,0}}$$

其中 $l_{i,0}$ 是绳索的原始的长度

弹性绳索建模——集中质量法

^7bd30c

这是很经典的一种方法，通过将绳索离散为多段单元，并将质量集中到每段的端点上，利用线性变形的假设将端点之间通过弹簧连接，最终通过拉格朗日方法建立动力学模型

@caverlyDynamicModelingPassivityBased2015

动力学模型

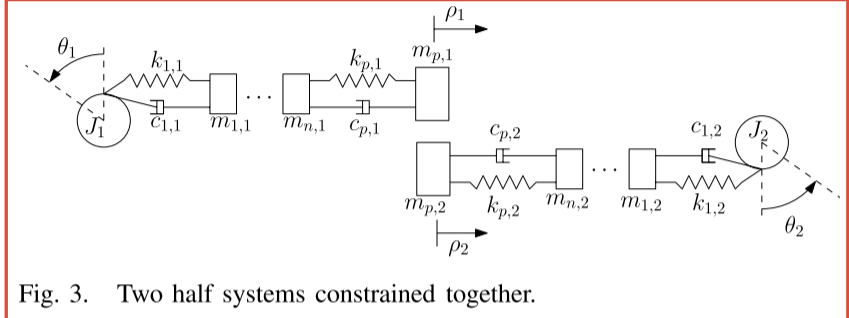
note

我们只看其中一半模型

将 winch 外的绳索划分为 n 段，取系统坐标为：

$$q^T=\left[\begin{array}{cc}\theta & {q_e}^T\end{array}\right]$$

其中

$$q_e={\left[\begin{array}{ccccc}{x}_1& x_2& \cdots & x_n& x_p\end{array}\right]}^T$$

是划分段数的 相对坐标，$x_p$ 代表末端坐标的相对坐标

note

事实上如果你愿意，将末端那一节勉强也能看成是第n+1段，只不过质量有所变化

可以将系统的动能和使能以及 Rayleigh dissipation 表示为：

$$T=\frac{1}{2}{\dot{q}}^{T}M\dot{q},V=\frac{1}{2}{q}^{T}Kq,R=\frac{1}{2}{\dot{q}}^{T}D\dot{q}$$

其中 $M=M^T=M_p+M_w+{\sum }_{i=1}^n{M}_i$，$K^T=\mathrm{diag}\left\{0,k_1,k_2,\cdots ,k_n,k_p\right\}$，$D^T=\mathrm{diag}\left\{0,c_1,c_2,\cdots ,c_n,c_p\right\}$，且：

$$M_p=m_p\left[\begin{array}{cc}{r}^2& -r{1_{1:n+1}}^T\\ -r{1}_{1:n+1}& 1_{1:n+1}{1_{1:n+1}}^T\end{array}\right]$$

$$M_w=\left[\begin{array}{cc}{J}_1& \\ & \end{array}\right]$$

$$M_i=m_i\left[\begin{array}{cc}{r}^2& -r{1_{1:i}}^T\\ -r{1}_{1:i}& 1_{1:i}{1_{1:i}}^T\end{array}\right]$$

其中

$$1_{i:j}={\left[\begin{array}{ccccccccc}0& \cdots & 0& \underset{i}{\underbrace{1}}& \cdots & \underset{j}{\underbrace{1}}& 0& \cdots & 0\end{array}\right]}^T$$

对离散的绳索有：

$$m_1=\sigma A\left(\frac{L}{n}-r\theta \right)$$

$$m_i=\sigma A\frac{L}{n},i=2,3,\cdots ,n$$

$$k_1=\frac{EA}{\frac{L}{n+1}-r\theta }$$

$$k_i=\frac{EA}{\frac{L}{n+1}},i=2,3,\cdots ,n,p$$

$$J_1=J_w+\sigma A{r}^3\theta$$

其中 $J_w$ 是 winch 转动惯量

note

这里其实是有点暗示角度不能太大，否则 $m_1<0$？

那么为什么不定义成：

$$m_1=\sigma A\left(\frac{L-r\theta }{n}\right)$$

进一步建立拉格朗日方程可以得到：

$$M\ddot{q}+D\dot{q}+Kq=\hat{b}\tau +f_{non}$$

其中

$$\hat{b}={\left[\begin{array}{cc}1& 0\end{array}\right]}^T$$

代表了施加在 winch 上的转矩系数

$$f_{non}=-\dot{M}\dot{q}+{\left(\frac{\tilde{\partial }}{\tilde{\partial }q}\left(\frac{1}{2}{\dot{q}}^{T}M\dot{q}\right)\right)}^T-{\left(\frac{\tilde{\partial }}{\tilde{\partial }q}\left(\frac{1}{2}{q}^{T}Kq\right)\right)}^T$$

这一些项是在考虑了 winch 之后，由于第一段绳子的质量和刚度改变带来的非线性项：

$$\dot{M}=\left[\begin{array}{ccc}0& -{\dot{m}}_{1}r& 0\\ -{\dot{m}}_{1}r& {\dot{m}}_1& 0\\ 0& 0& 0\end{array}\right]$$

$${\dot{m}}_1=-r\sigma A\dot{\theta }$$

$${\left(\frac{\tilde{\partial }}{\tilde{\partial }q}\left(\frac{1}{2}{\dot{q}}^{T}M\dot{q}\right)\right)}^T=-\frac{1}{2}\sigma Ar\left[\begin{array}{c}-2r\dot{\theta }{\dot{x}}_1+{{\dot{x}}_1}^2\\ 0\end{array}\right]$$

$${\left(\frac{\tilde{\partial }}{\tilde{\partial }q}\left(\frac{1}{2}{q}^{T}Kq\right)\right)}^T=\left[\begin{array}{c}\frac{1}{2}\frac{EAr}{{\left(\frac{L}{n+1}-r\theta \right)}^2}{x_1}^2\\ 0\end{array}\right]$$

note

注意如果将位移分散到每一段中，即

$$m_i=\sigma A\left(\frac{L}{n}-r\theta \right)$$

那么计算$F_{non}$的时候会复杂很多...全部质量非线性

数值仿真

仿真参数：

%% INIT PARAMS

mp = 1; % 负载质量
r = 0.5; % 滑轮半径
Jw = 1.39e-1; % winch 转动惯量
L = 5; % 绳索原长
A = 17.95e-6; % 绳索截面面积
rho = 2200; % 绳索密度
E = 500e6; % 弹性模量
tau = @(t) 1; % 转矩
f = @(t) 0; % 外力

n = 5; % 瑞利基数

% damper coefficients
D = zeros(n+2);

% params
P.r = r;
P.rho = rho;
P.A = A;
P.Jw = Jw;
P.mp = mp;
P.D = D;
P.tau = tau;
P.f = f;
P.L = L;
P.E = E;
P.n = n;

t_end = 1;
tspan = [0 t_end];
simu_num = 500;

仿真代码：

q0 = zeros(n+2,1);
dq0 = zeros(n+2,1);
y0 = [q0;dq0];
sol = ode45(@(t,y) CableLMModel(t, y, P),tspan,y0)
x = linspace(0,t_end,simu_num);
y = deval(sol,x);
LM_theta = y(1, :);
LM_dx = sum(y(2:(n+2), :), 1);
LM_xp = L - r.*LM_theta + LM_dx;
LM_figPlot(x, LM_theta, LM_xp, LM_dx)

• CableLMModel
• SingleCableSim

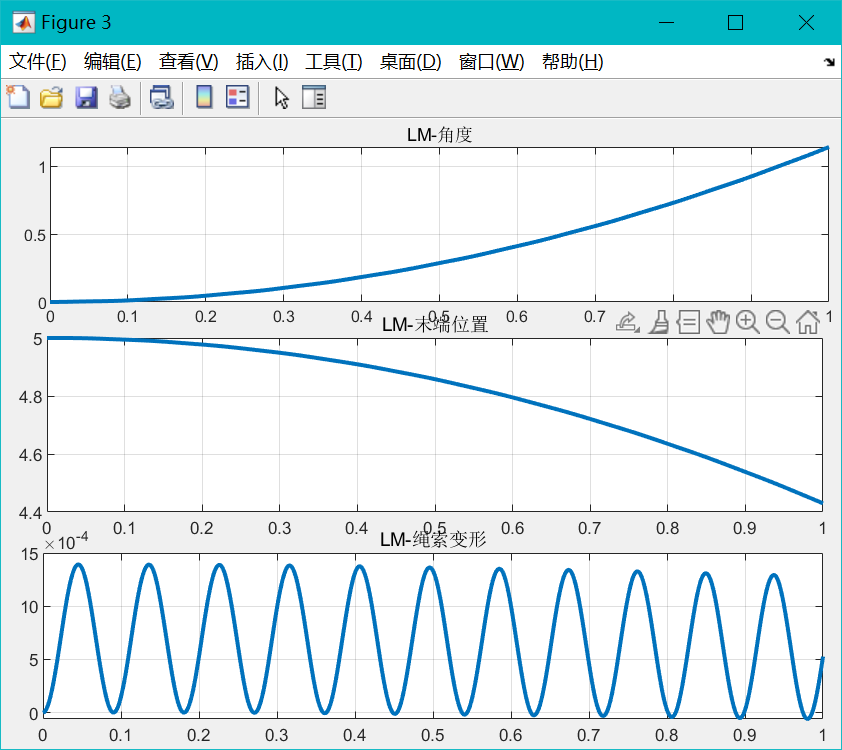
弹性绳索建模——Rayleigh-Ritz 方法

参考 @gosselinCableDrivenParallelRobots2018 的 P14：Modelling of Flexible Cable-Driven Parallel Robots Using a Rayleigh-Ritz Approach

关于 Rayleigh-Ritz 方法可以参考： Chap3 弹性体振动，Chap3 弹性体振动

模型基础

p16r57

其中 $i,w,c$ 分别是世界坐标系，winch 坐标系和绳索坐标系

Payload 到 winch 切点距离为 $l_i$，winch 转角为 $\theta$，绳子名义的初始长度 (总长) 为 $L$，那么有：$l_i=L-r\theta$。定义 时不变的坐标 x 为绳子上一点相对 C 点的长度，$\beta$ 为 winch 上绳子相对竖直位置的角度， $x_p$ 是 payload 中心相对 winch 中心在 $i_1$ 方向的位置

note

注意这里的$l_i$是不考虑变形时候的payload到切点的距离，而$x_p$是考虑变形后实际的payload到切点的距离

选取 Ritz 基为：

$${\Psi }_{oe}\left(x,l_i\right)=\left[\begin{array}{ccc}\sin \left(\frac{\pi \left(x-L+l_i\right)}{2l_{\mathrm{i}}}\right)& \sin \left(\frac{2\pi \left(x-L+l_i\right)}{2l_{\mathrm{i}}}\right)& \cdots \end{array}\right]$$

^eqn-ritz-basis

其中 $x-L+l_i=x-r\theta$

我们根据 Ritz 基给出绳子在任一点上的变形量为：

$$w\left(x,t\right)={\Psi }_{oe}\left(x,l_i\left(t\right)\right)q_e\left(t\right)$$

这里的 $q_e$ 就是弹性变形相对 Ritz 基的时变的坐标，有 n 个自由度

从而根据上面的分析将整个系统的广义坐标表示为：

$$q^T=\left[\begin{array}{ccc}\theta & {q_e}^T& x_p\end{array}\right]$$

^eqn-generalized-coordinates

note

我知道这么选取广义坐标是不独立的，但这么建立动力学模型，在后面如果涉及到多索机构的时候可以方便的添加约束上去，从而保证独立性

动力学模型

使用拉格朗日方程可以建立起动力学模型：

Assumption

在 inertial fram(i) 下进行分析

首先对 winch 上的绳子进行分析：

一个单位质量元 $dm$ 对应的坐标可以表示为：

$$\begin{array}{l}{r}_i^{dmi}={\left[\begin{array}{ccc}-r\sin \beta & r\cos \beta & 0\end{array}\right]}^T\\ v_i^{dmi}={\left[\begin{array}{ccc}-r\dot{\beta }\cos \beta & -r\dot{\beta }\sin \beta & 0\end{array}\right]}^T\end{array}$$

从而动能可以表示为：

$$\frac{1}{2}{\int }_{C_w}{v}_i^{dmi}\cdot v_i^{dmi}\mathrm{d}m=\frac{1}{2}{\int }_0^{r\theta }{v}_i^{dmi}\cdot v_i^{dmi}\rho A\mathrm{d}x=\frac{1}{2}{\dot{q}}^T{M}_{cw}\dot{q}$$

其中 $M_{cw}=\mathrm{diag}\left\{r^3\rho A\theta ,0\right\}\in {\mathbb{R}}^{\left(n+2\right)\times \left(n+2\right)}$

类似的可以得到 winch 和 payload 的动能：

$$\begin{array}{c}{T}_w=\frac{1}{2}{\dot{q}}^T{M}_w\dot{q}\\ T_p=\frac{1}{2}{\dot{q}}^T{M}_p\dot{q}\end{array}$$

其中 $M_w=\mathrm{diag}\left\{J_w,0\right\}$，$M_p=\mathrm{diag}\left\{0,m_p\right\}$

对 winch 外的绳子进行分析：

$$\begin{array}{l}{r}_i^{dmi}={\left[\begin{array}{ccc}x-r\theta +\Psi q_e& r& 0\end{array}\right]}^T\\ v_i^{dmi}={\left[\begin{array}{ccc}-r\dot{\theta }+\dot{\Psi }{q}_e+\Psi {\dot{q}}_e& 0& 0\end{array}\right]}^T\end{array}$$

其中

$$\begin{array}{c}\dot{\Psi }=\left(-r\dot{\theta }\right)\frac{\partial \Psi }{\partial l_i}\\ \frac{\partial \Psi }{\partial l_i}=\left[\begin{array}{ccc}-\frac{\pi x}{2{l_i}^2}\cos \left(\frac{\pi x}{2l_i}\right)& -\frac{2\pi x}{2{l_i}^2}\cos \left(\frac{2\pi x}{2l_i}\right)& \cdots \end{array}\right]\end{array}$$

从而可以得到 unwarpped cable 的动能为：

$$\frac{1}{2}{\int }_{C_{l_i}}{v}_i^{dmi}\cdot v_i^{dmi}\mathrm{d}m=\frac{1}{2}{\int }_{C_{l_i}}{\left(-r{\dot{\theta }}_1\frac{\partial \Psi }{\partial l_{\mathrm{i}}}{q}_e+\Psi {\dot{q}}_e-r{\dot{\theta }}_1\right)}^2\mathrm{d}m$$

从而可以将其写成一个二次型的形式：

$$\begin{array}{l}{T}_C=\frac{1}{2}{\dot{q}}^T{M}_{ce}\dot{q}\\ M_{ce}={\int }_{L-l_i}^L\rho A\left[\begin{array}{ccc}{r}^2\left(1+2\frac{\partial \Psi }{\partial l_i}{q}_e+{q_e}^T{\left(\frac{\partial \Psi }{\partial l_i}\right)}^T\frac{\partial \Psi }{\partial l_i}{q}_e\right)& -r\left(1+{q_e}^T{\left(\frac{\partial \Psi }{\partial l_i}\right)}^T\right)\Psi & 0\\ \ast & \ast & 0\\ \ast & \ast & 0\end{array}\right]\mathrm{d}x\end{array}$$

通过变换 $z=x-L+l_i$，可以得到问题方程被简化为：

$${\mathbf{M}}_{ce}=\rho A\left[\begin{array}{ccc}{r}^2\left({\ell }_i+2{\mathbf{\Lambda }}_1{\mathbf{q}}_e+\frac{1}{{\ell }_i}{\mathbf{q}}_e^{\top }{\mathbf{\Lambda }}_{11}{\mathbf{q}}_e\right)& -r\left({\ell }_i{\mathbf{\Lambda }}_2+{\mathbf{q}}_e^{\top }{\mathbf{\Lambda }}_{12}\right)& 0\\ \ast & {\ell }_i{\mathbf{\Lambda }}_{22}& 0\\ \ast & \ast & 0\end{array}\right]$$

其中 ${\mathbf{\Lambda }}_1={\int }_0^{l_i}\frac{\partial \Psi }{\partial l_i}\mathrm{d}z$，${\mathbf{\Lambda }}_{11}=l_i{\int }_0^{l_i}{\left(\frac{\partial \Psi }{\partial l_i}\right)}^T\frac{\partial \Psi }{\partial l_i}\mathrm{d}z$，${\mathbf{\Lambda }}_{12}=l_i{\int }_0^{l_i}{\left(\frac{\partial \Psi }{\partial l_i}\right)}^T\Psi \mathrm{d}z$，${\mathbf{\Lambda }}_2=\frac{1}{l_i}{\int }_0^{l_i}\Psi \mathrm{d}z$，${\mathbf{\Lambda }}_{22}=\frac{1}{l_i}{\int }_0^{l_i}{\Psi }^T\Psi \mathrm{d}z$

note

这一质量方程的简化是通过选取合适的这种三角函数基完成的

对绳子的势能可以通过弹性变形得到：

$$\frac{1}{2}{\int }_{L-{\ell }_i}^{L}EA{\left(\frac{\partial \left({\mathbf{\Psi q}}_e\right)}{\partial x}\right)}^2\mathrm{d}x=\frac{1}{2}{\mathbf{q}}_e^{\top }{\int }_0^{{\ell }_i}EA{\left(\frac{\partial \mathbf{\Psi }}{\partial x}\right)}^{\top }\left(\frac{\partial \mathbf{\Psi }}{\partial x}\right)\mathrm{d}z{\mathbf{q}}_e=\frac{1}{2}{\mathbf{q}}^{\top }\mathbf{Kq}$$

其中 $K=\mathrm{diag}\left\{0,EA{\Lambda }_{33}/l_i,0\right\},{\Lambda }_{33}=l_i{\int }_0^{l_i}{\left(\frac{\partial \Psi }{\partial x}\right)}^T\frac{\partial \Psi }{\partial x}\mathrm{d}z$

为了引入绳索自然的阻尼项，加入 Rayleigh dissipation 为：

$$R=\frac{1}{2}{\dot{q}}^{T}D\dot{q},D=\mathrm{diag}\left\{0,c_1,c_2,\cdots ,c_n,0\right\}$$

从而系统的拉格朗日方程导出的动力学方程为：

$$M_e\ddot{q}+D\dot{q}+Kq=\hat{b}\tau +f_{non}$$

其中

p18r47 ^eqn-dynamic-model

p19r47

note

注意，到目前为止，末端的payload还没有被连接到绳索末端，需要后面增加constraints

基于能量的模型简化

1. 注意到仿真中，unwarpped cable 的动能 $T_{ce}=\frac{1}{2}{\int }_{L-l_i}^L{\left(-r{\dot{\theta }}_1+\Psi {\dot{q}}_e+\dot{\Psi }{q}_e\right)}^2\rho A\mathrm{d}x$，其中的 $\dot{\Psi }{q}_e$ 比 $\Psi {\dot{q}}_e$ 小了很多 (约 $10^{-2}$ 量级)，从而忽略这一项，进而忽略了 ${\Lambda }_1,{\Lambda }_{11},{\Lambda }_{12}$这几项，方程简化为：

p19r33

其中

$${\Lambda }_2\left(k\right)=\frac{4{\sin }^2\left(\frac{\pi k}{4}\right)}{\pi k}$$

$${\Lambda }_{22}=\{\begin{array}{l}\frac{1}{2}\left(1-\frac{\sin \left(\pi i\right)}{\pi i}\right),i=j\\ \frac{\frac{\sin \left(\frac{1}{2}\pi (i-j)\right)}{i-j}-\frac{\sin \left(\frac{1}{2}\pi (i+j)\right)}{i+j}}{\pi },i\ne j\end{array}$$

$${\Lambda }_{33}=\{\begin{array}{l}\frac{1}{8}\pi i(\pi i+\sin (\pi i))=\frac{{\left(\pi i\right)}^2}{8},i=j\\ \frac{1}{4}\pi ij\left(\frac{\sin \left(\frac{1}{2}\pi (i-j)\right)}{i-j}+\frac{\sin \left(\frac{1}{2}\pi (i+j)\right)}{i+j}\right),i\ne j\end{array}$$

$\Lambda (k)$ 代表第 k 个元素

连接约束

在 ^eqn-dynamic-model 中，选取的广义坐标并不是独立的，因此需要对其施加约束来保证问题的求解：

考虑到初始选取的广义坐标为：

^eqn-generalized-coordinates

从而考虑其缺失的一个约束，即末端位置 $x_p$ 和前 2 个坐标存在关系：

$$x_p=\Psi \left(L,l_i\right)q_e-r\theta \Rightarrow {\dot{x}}_p=\Psi \left(L,l_i\right){\dot{q}}_e-r\dot{\theta }$$

note

这里的约束其实感觉不是对时间的导数，有点像虚位移的感觉=>虚功那一套

从而构造约束 $\Xi$ 为：

$$\begin{array}{c}\Xi \dot{q}=0,\Xi =\left[\begin{array}{ccc}{J}_{\theta }& J_e& -1\end{array}\right]\\ J_{\theta }=-r,J_e=\Psi \left(L,l_i\right)\end{array}$$

我们考虑构造带约束的拉格朗日系统为：

$$M\ddot{q}+D\dot{q}+Kq=\hat{b}\tau +f_{non}+{\Xi }^T\lambda$$

其中 $\lambda$ 为拉格朗日乘子，用于约束系统

我们考虑构造新的广义坐标为：

$$z^T=\left[\begin{array}{cc}\theta & {q_e}^T\end{array}\right]$$

使得其在约束 $\Xi$ 的零空间中，即：

$$q=Rz,\dot{q}=R\dot{z},\Xi R=0$$

通过约束可以直接得到 R 为：

$$R=\left[\begin{array}{cc}1& 0\\ 0& 1\\ J_{\theta }& J_e\end{array}\right]$$

从而考虑新系统：

$$\begin{array}{c}{R}^{T}MR\ddot{z}+R^{T}DR\dot{z}+R^{T}KRz=R^T\hat{b}\tau +R^T{f}_{non}+R^T{\Xi }^T\lambda \\ \Rightarrow M_{zz}\ddot{z}+D_{zz}\dot{z}+K_{zz}z={\hat{b}}_{zz}\tau +f_{non,zz}\end{array}$$

新系统下就可以直接进行仿真了

remark

这么做的主要优势是将约束放在最后进行考虑，对多索耦合的系统可以按照范式方便的进行拓展

note

对比弹性绳索建模——集中质量法，集中质量法构造的单索模型就不需要施加约束，但是多索的话还是需要的

仿真结果

仿真条件为：

mp = 5;      % 负载质量
r = 0.5;       % 滑轮半径
Jw = 1.39e-1;  % winch 转动惯量
L = 20;        % 绳索原长
A = 17.95e-6;   % 绳索截面面积
rho = 2200;     % 绳索密度
E = 500e6;      % 弹性模量
n = 5;          % 瑞利基数

% damper coefficients
D = zeros(n+2);
% init conditions: (n+2)x2
% q = [\theta, q_e^T]
% y = [q;dq]
q0 = zeros(n+1,1);
dq0 = zeros(n+1,1);
y0 = [q0;dq0];

仿真时长 10s，250 步

note

这里的瑞利基选取5个，而不选取更高阶是因为高阶的基计算出的 ${\Lambda }_{22}$ 会有很大的条件数，测试发现的是:

• 5阶：9.6306e+04
• 10阶：1.4618e+12
• 20阶：9.0865e+16

因此不能算高了，会导致数值计算不稳定

不对拉结果为：

tau = @(t) 1;        % 转矩
f = @(t) 0;      % 外力

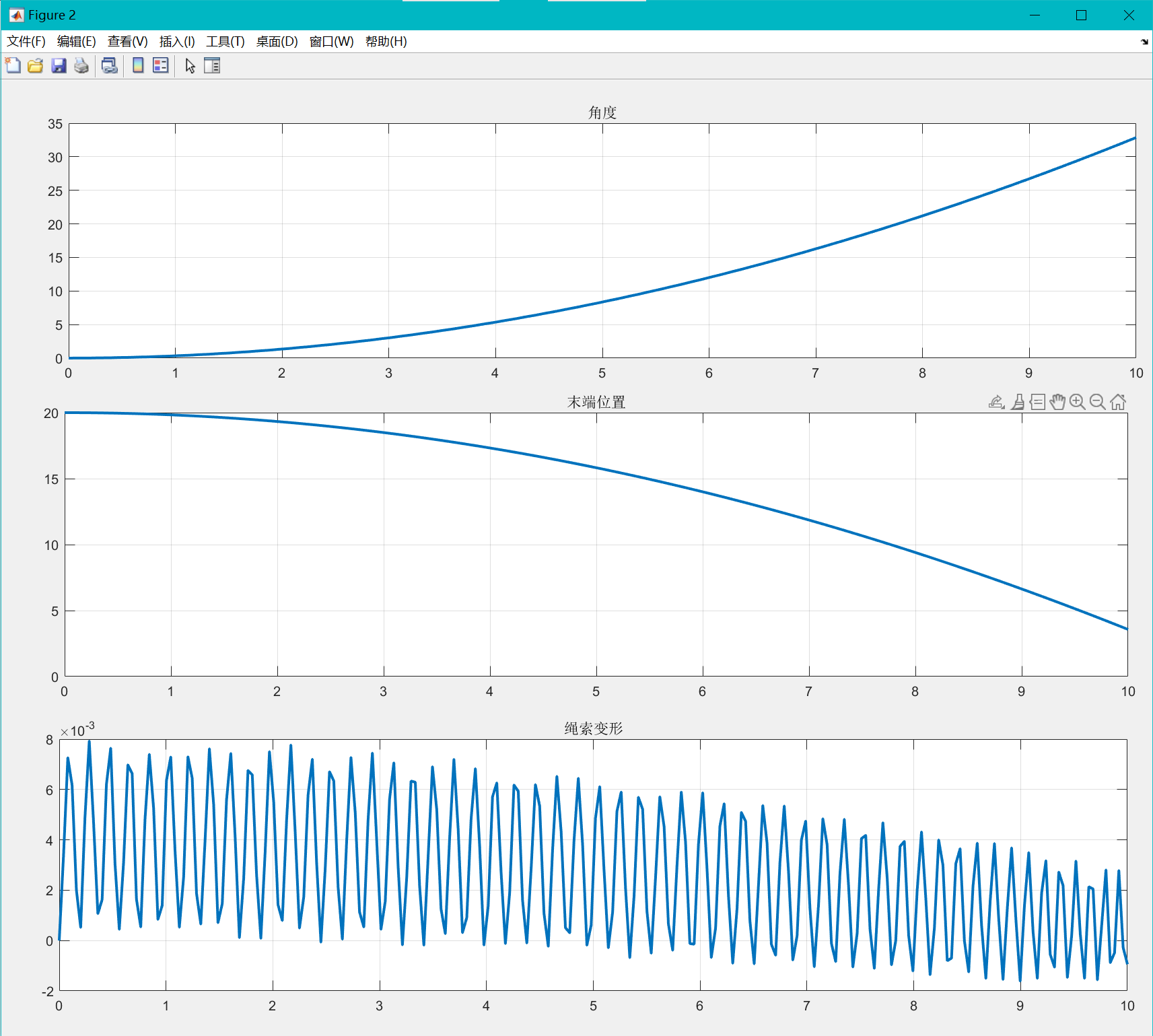
对拉拉力为：

tau = @(t) 1;        % 转矩
f = @(t) tau(t)/r;      % 外力

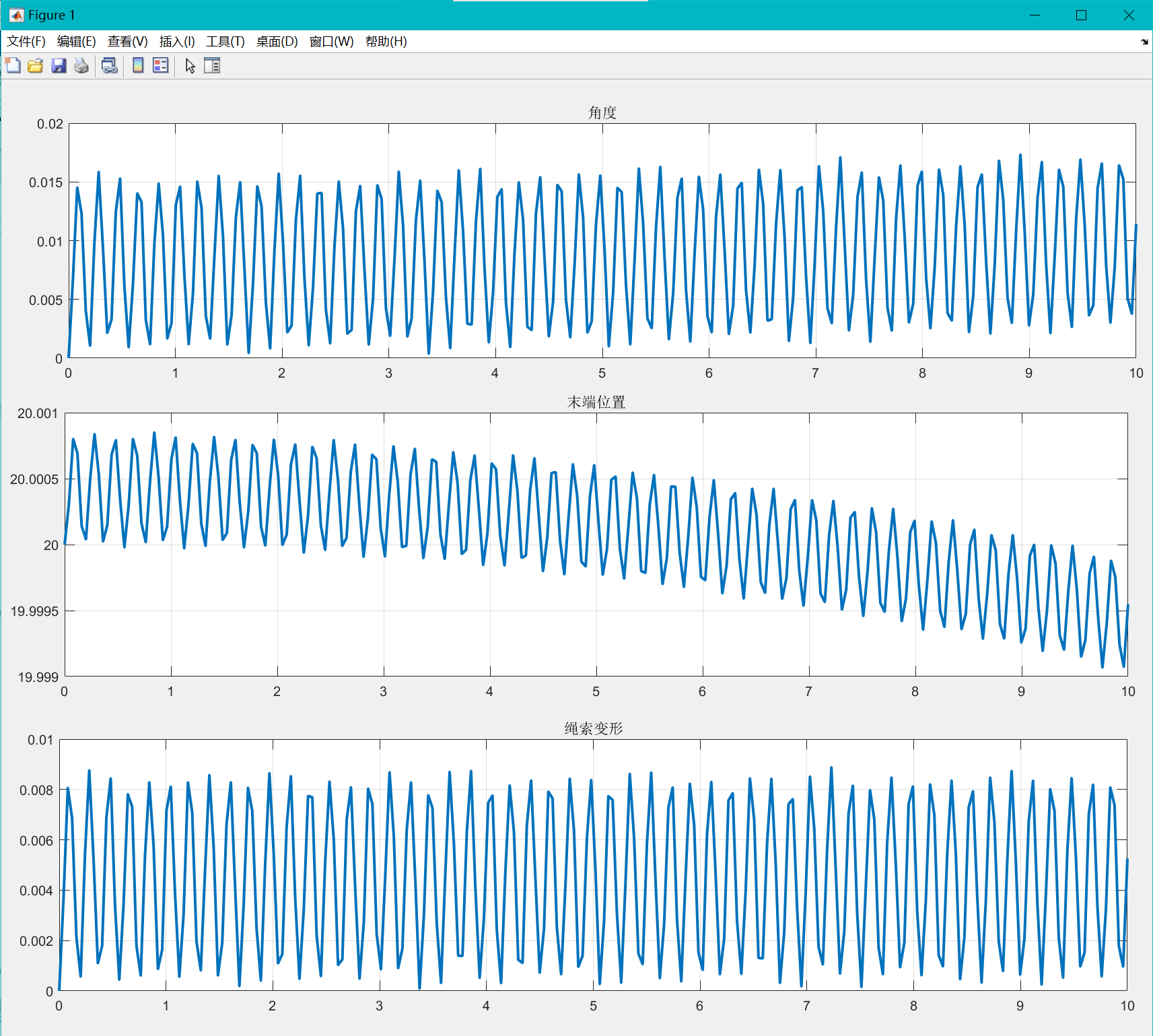
至少说明施加的力还是有效果的

仿真代码参考：

• CableRRModel
• SingleCableSim

符号计算参考：

• SymbolCal

对比：集中质量 Vs 瑞雷 - 李兹

从理论推导上来看，集中质量法 是 瑞雷李兹法 的一种特例，无非是选取的基函数变成了分段的单位函数，这一改变的影响体现在推导瑞雷李兹法过程中的 $\Lambda$ 上

注意到建立的模型大概为：

单索并联机构动力学模型 2022-09-21 14

因此对集中质量法 (至少我参考的文章)，其要求 winch 转角 $\theta$ 不能太大，否则超过了第一段的长度会导致计算错误（比如出现负质量、负刚度），特别地：

$${\theta }_{\max }⩽\frac{L}{\left(n+1\right)r}$$

note

额外选取一个最简单的模型：绳索认为完全刚性，可以立即传导双向的力和力矩，忽略绳子的质量，那么动力学模型为：

$$\begin{array}{rl}\tau -rf& =\left(J+M{r}^2\right)\ddot{\theta }\\ x_p& =L-r\theta \end{array}$$

选取基本的仿真参数为：

mp = 1; % 负载质量
r = 0.5; % 滑轮半径
Jw = 1.39e-1; % winch 转动惯量
L = 5; % 绳索原长
A = 17.95e-6; % 绳索截面面积
rho = 2200; % 绳索密度
E = 500e6; % 弹性模量

n = 5; % 瑞利基数

% damper coefficients
D = zeros(n+2);

t_end = 1;
tspan = [0 t_end];
simu_num = 500;

带入可以计算得到：

$${\theta }_{\max }⩽\frac{L}{\left(n+1\right)r}=\frac{5}{6\times 0.5}=1.66667$$

代码可以参考：

• SingleCableSim

单向转矩

对单向转动的情况，考虑：

tau = @(t) 1; % 转矩
f = @(t) 0; % 外力

进行仿真有：

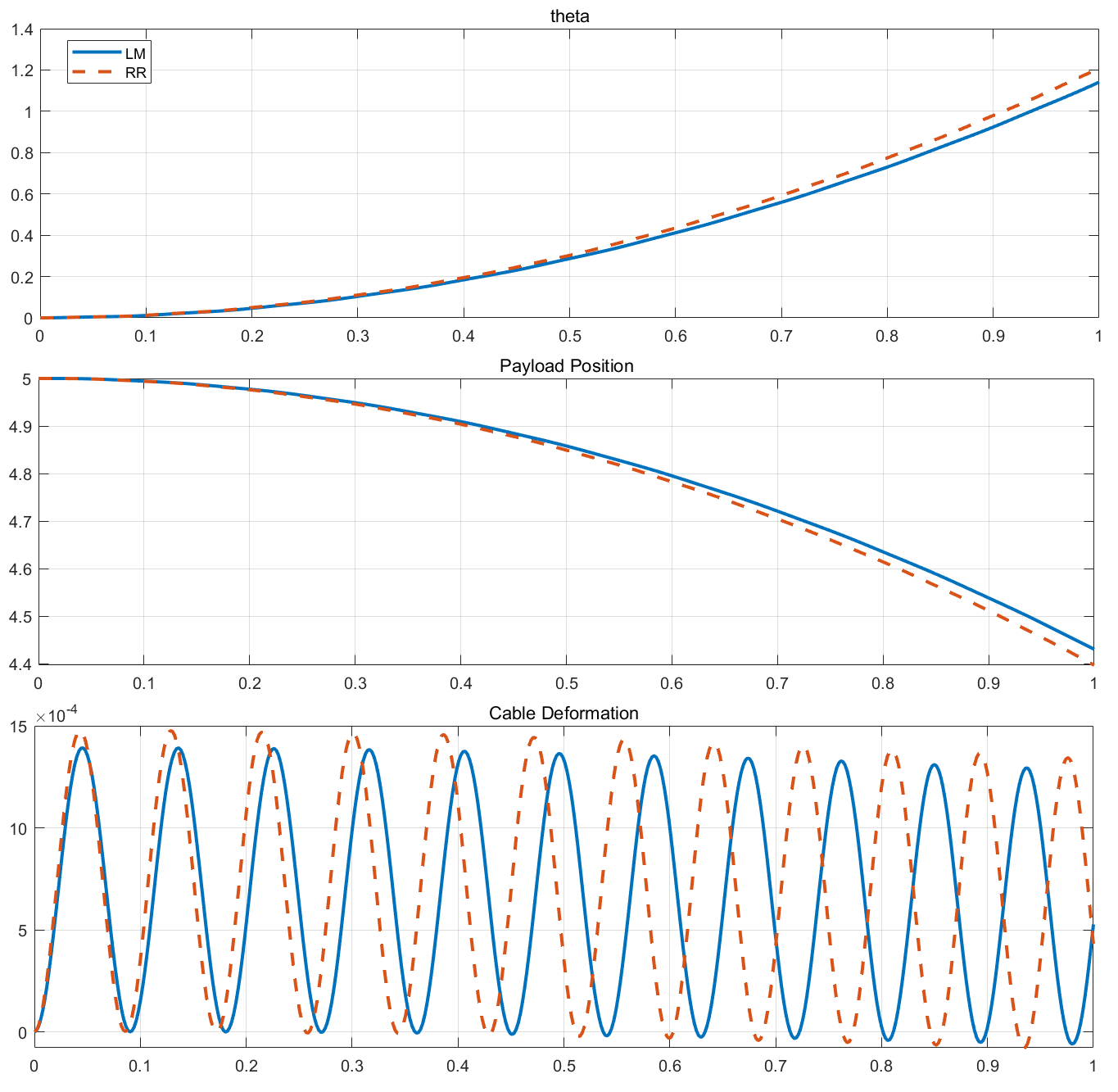
基本上比较贴合

附上和完全刚性的结构进行对比的图片：

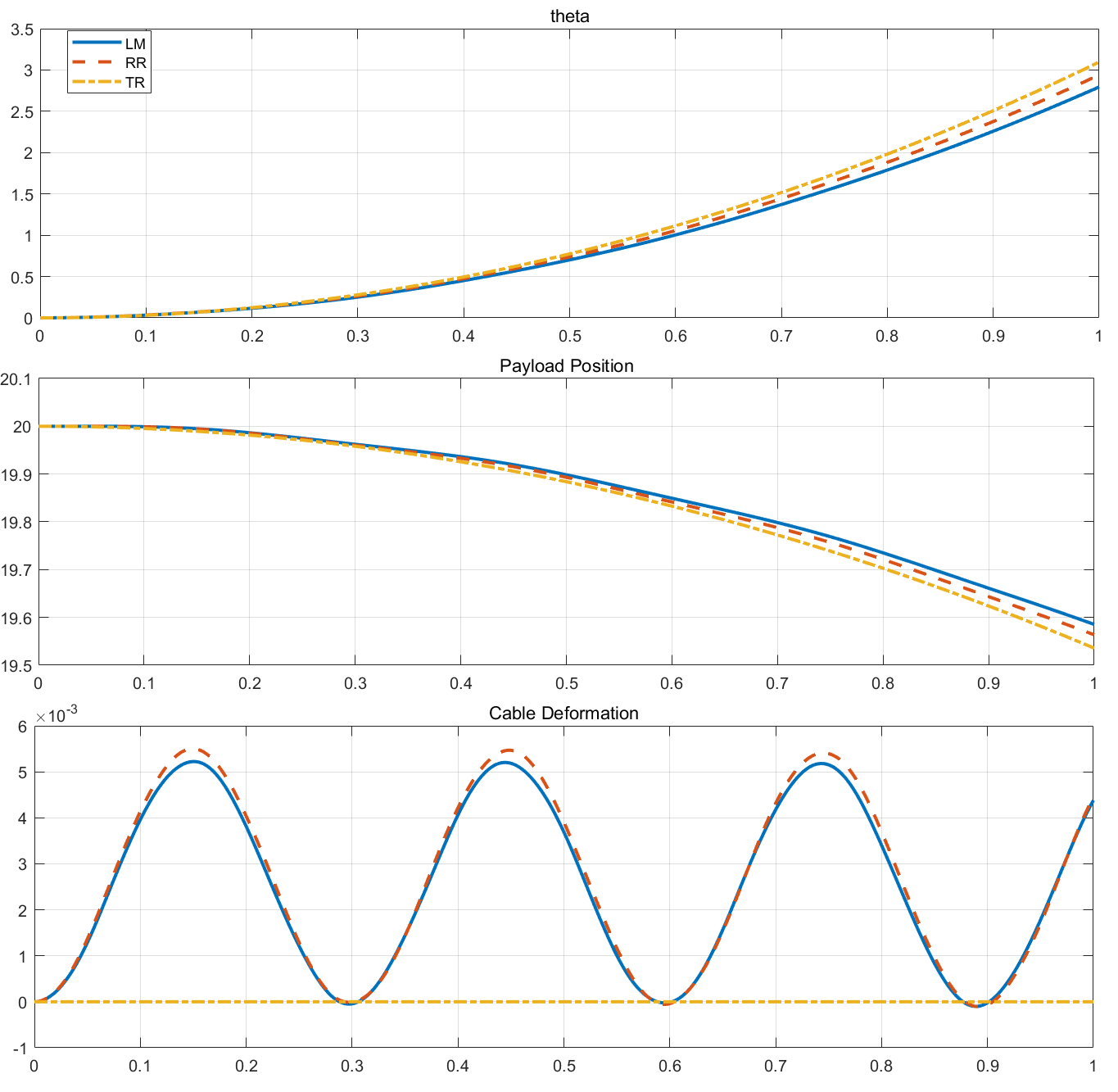
单向拉力

tau = @(t) 0; % 转矩
f = @(t) 1; % 外力

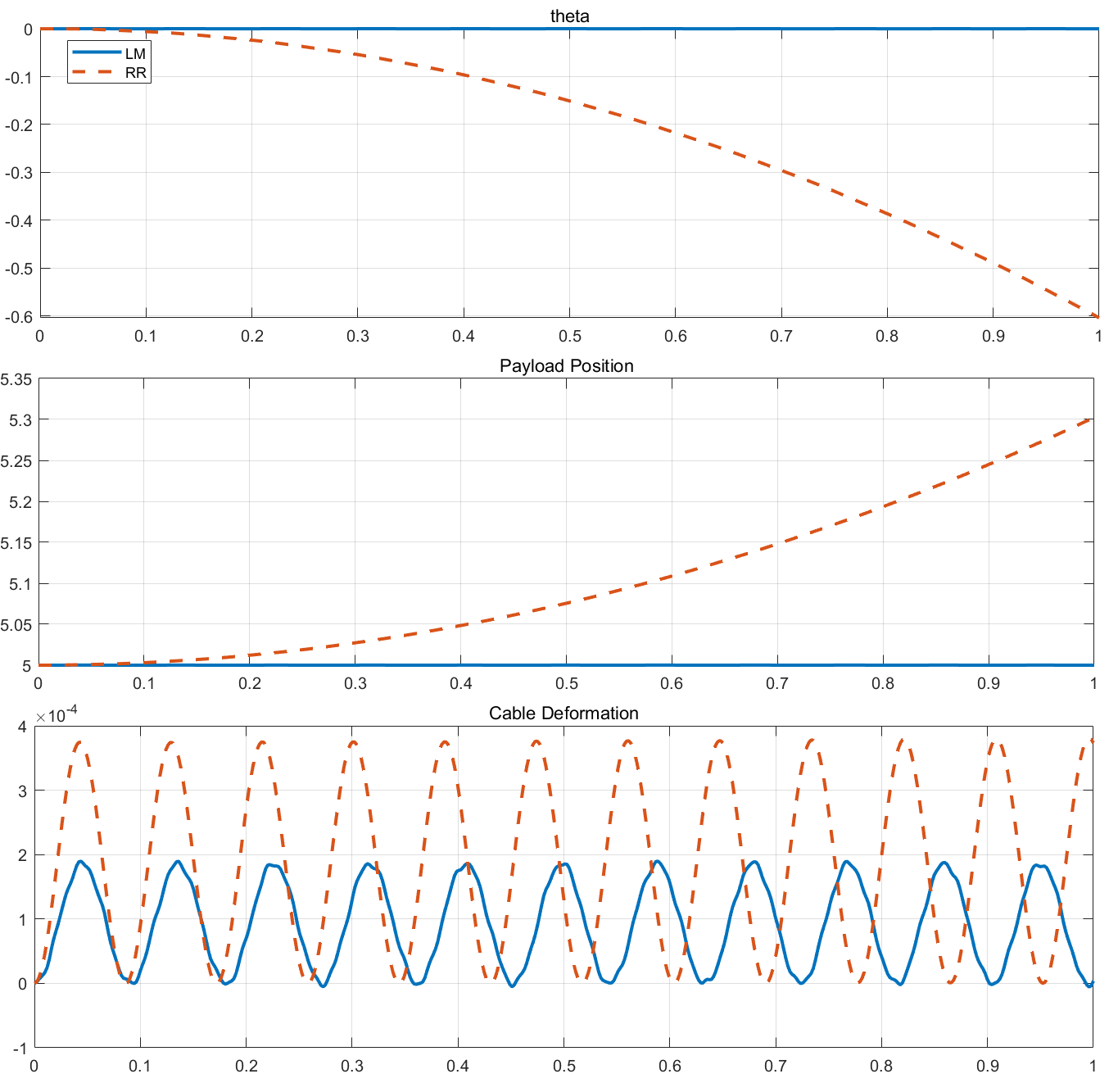
可以发现，LM 角度基本不变，这是因为按照设计他就不能按照这个方向被拉；而反过来的 RR 就可以被拉伸，产生反方向的转动

双向对拉

tau = @(t) 1; % 转矩
f = @(t) tau(t)/r; % 外力

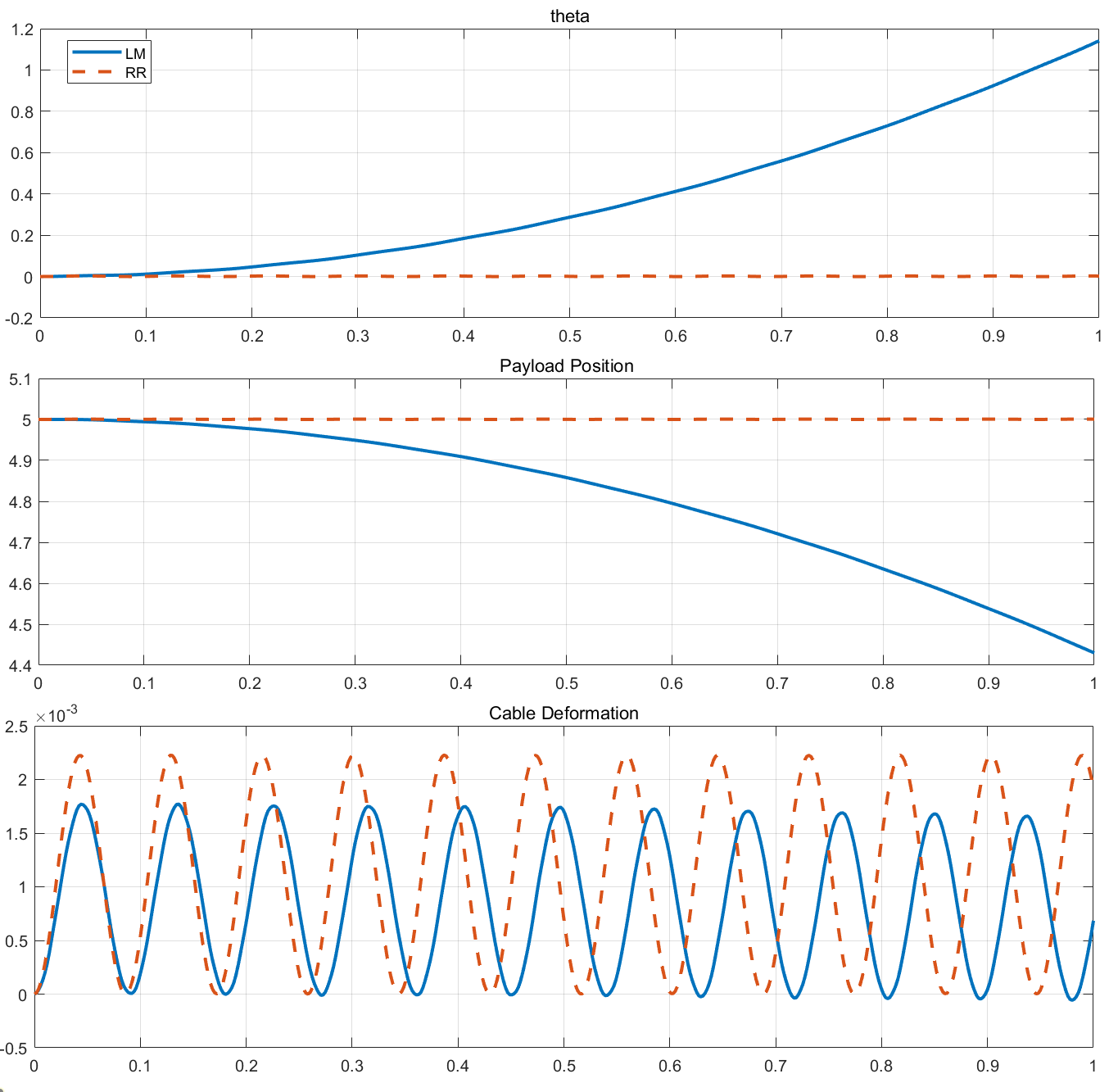
可以发现 RR 基本是满足期望的，但是对 LM 就不太对，这应该是程序 Bug，还没想到为什么

大力矩拉动

tau = @(t) 5; % 转矩
f = @(t) 0; % 外力

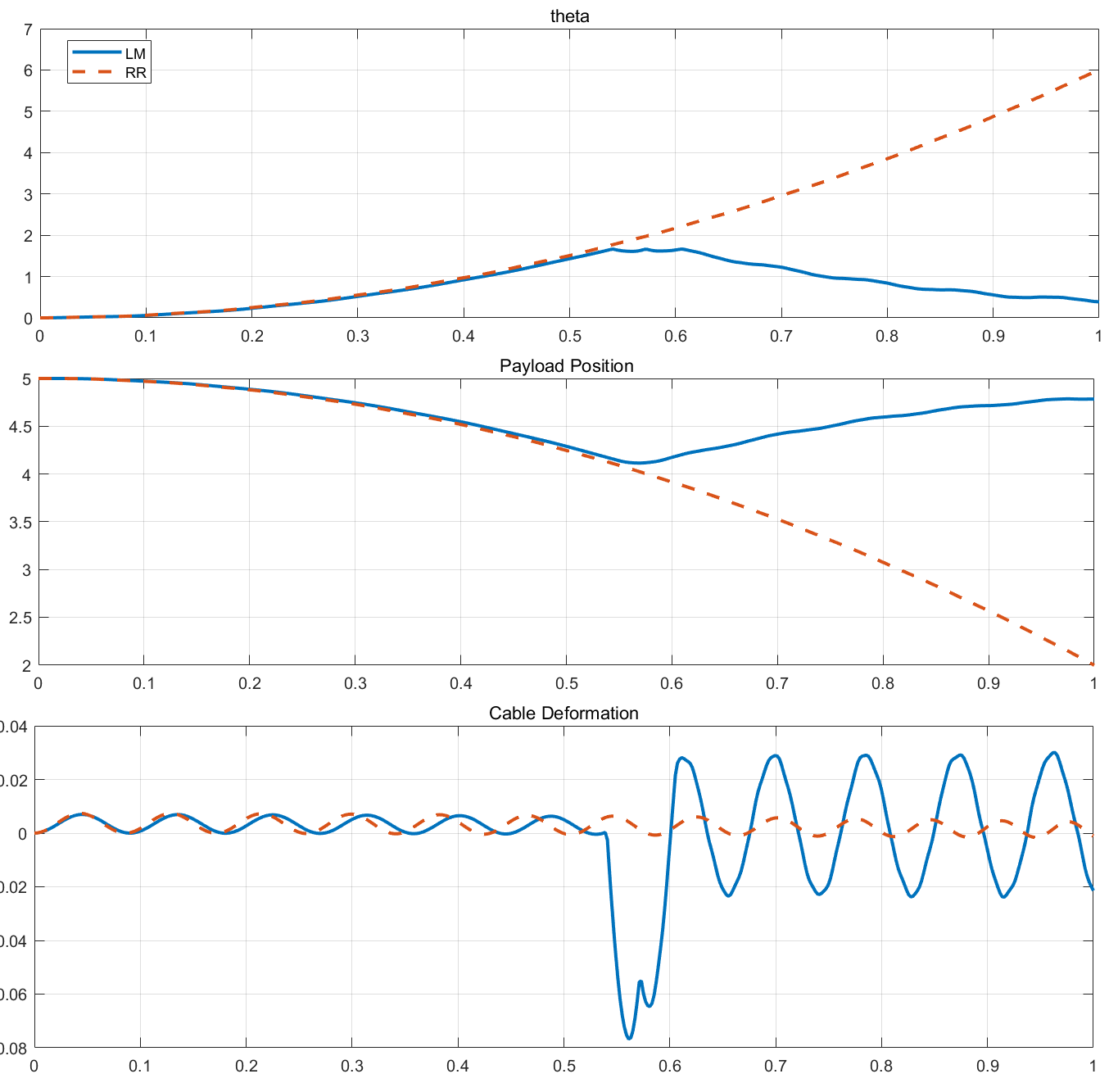
可以发现，LM 模型在角度为 1.6 度左右的时候出现反向振动，这就是前面说的到了最大转动角度，出现了负质量和负刚度

如果更极端一点，取下面这样的条件：

mp = 1; % 负载质量
r = 0.1; % 滑轮半径
Jw = 1.39e-1; % winch 转动惯量
L = 5; % 绳索原长
A = 17.95e-6; % 绳索截面面积
rho = 2200; % 绳索密度
E = 500e6; % 弹性模量
tau = @(t) 5; % 转矩
f = @(t) 0; % 外力

仿真 5s 的结果：

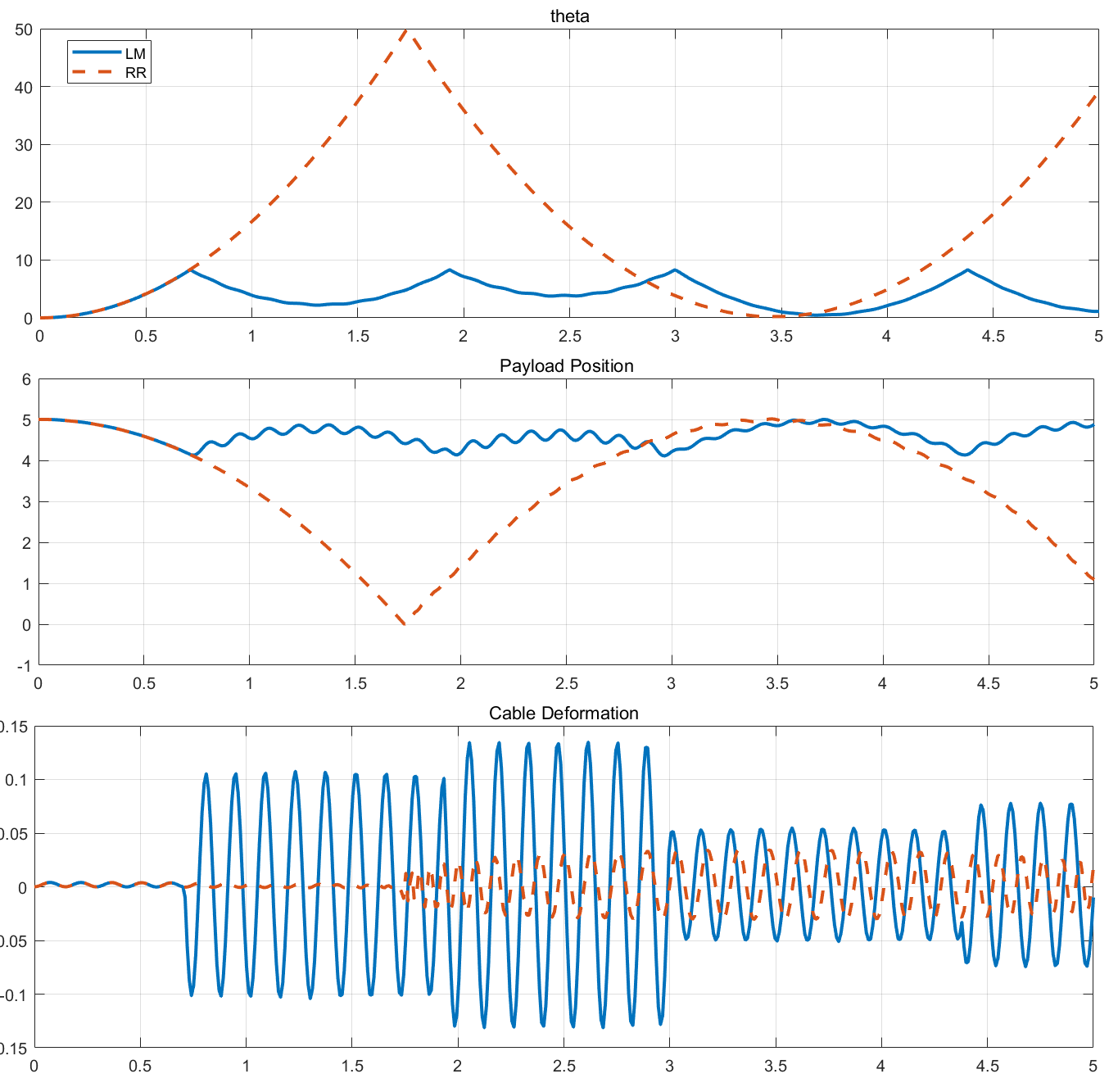
这里可以发现，RR 方法当其绳子全部缠到了 winch 上后就出问题了，这表明还是存在局限性的

note

不过确实这个情况很极端了

总结

对比 LM 方法和 RR 方法，有下面特点：

• RR 方法仿真的使用情况更广，多种情况下仿真
• RR 方法在低阶的时候稳定，高阶的话会出现高条件数的情况从而出现奇异
• 经过验证，无阻尼情况下，两个方法基本高阶和低阶解的结果基本一样

参考

引文

• @gosselinCableDrivenParallelRobots2018
• @pottCableDrivenParallelRobots2018

脚注