旋转矩阵求导

randolf2022年8月9日

大约 3 分钟

定义

我们知道，在机器人建立运动学/动力学模型时，很常见的情况是对旋转矩阵进行求导，因此特地拿出一节用作记录。

旋转矩阵可以有四元数的形式，也可以有欧拉角等形式，这里特指欧拉角形式。

旋转轴已知，假设只发生了旋转变换，上标 e 代表 inertial 坐标系，上表 b 代表随动的机体坐标系。

明确反对称矩阵表示为：

a \times b = S (a) b

其中，

S (a) = ⎣ ⎡ 0 a_{z} - a_{y} - a_{z} 0 a_{x} a_{y} - a_{x} 0 ⎦ ⎤

注意到，对仅旋转的向量 $r_{e}$ 有：

\frac{d r _{e}}{d t} = ω_{e} \times r_{e}

因此对旋转矩阵，将其看作为三个在地球坐标系下表达的列向量的组合，有：

\frac{d R _{e}^{b}}{d t} = \frac{d [ b _{1}^{e} b _{2}^{e} b _{3}^{e} ]}{d t} = [ω^{e} \times b_{1}^{e} ω^{e} \times b_{2}^{e} ω^{e} \times b_{3}^{e}] = [S (ω^{e}) b_{1}^{e} S (ω^{e}) b_{2}^{e} S (ω^{e}) b_{3}^{e}] = S (ω^{e}) R_{e}^{b}

其中， $R_{e}^{b}$ 代表从惯性系 e 转换到随体系 b 的旋转矩阵。

此外，具有如下性质：

S (R ω) = RS (ω) R^{T}

这本质上是一个线性变换在不同空间下的观察结果，也就是相似矩阵。

假定 R: A->B，按照题意 $ω$ 代表在 B 坐标系下观察到的角速度，那么参考矩阵坐标意义和变换意义中对相似矩阵的分析，有：

S (R ω) = (R^{T})^{- 1} S (ω) R^{T}

即上面的式子。

如论文 @caiModelAnalysisModified2021 模型所示，坐标系如下：

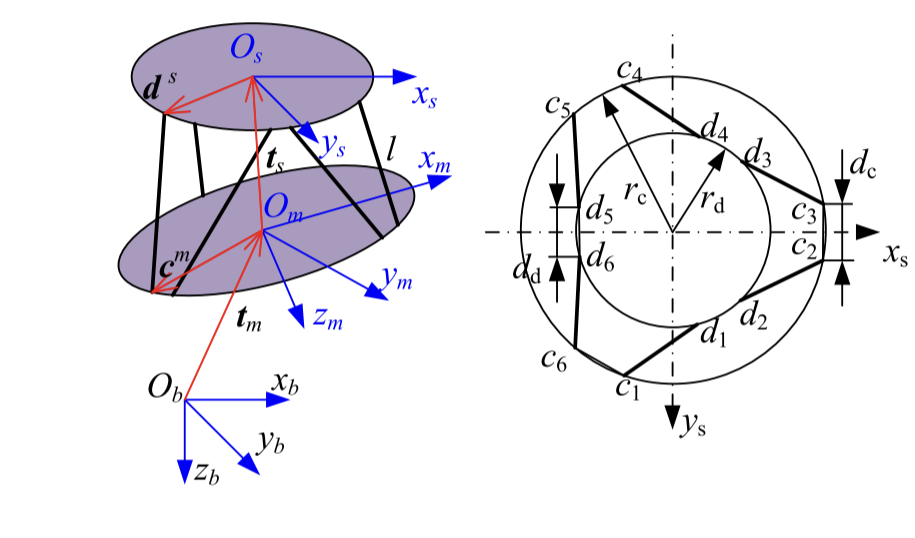
Pasted image 20220813172211

为了求向量 $c$ 和向量 $d$ 在全局坐标系 $O_{b}$ 下的速度，有（为了方便，下文不写向量符号了）：

c d = t_{m} + R_{bm} c^{m} = t_{m} + R_{bm} t_{s} + R_{bm} R_{m s} d^{s}

因此速度有微分为:

v_{c} v_{d} = \frac{d c}{d t} = \dot{t_{m}} + S (w_{m}) R_{bm} c^{m} = \frac{dd}{d t} = \dot{t_{m}} + S (w_{m}) R_{bm} t_{s} + R_{bm} \dot{t_{s}} + S (w_{m}) R_{bm} R_{m s} d^{s} + R_{bm} (S (w_{s m}) R_{m s} d^{s})

将坐标系转换到坐标系 m 上，得到结果：

c d = R_{bm}^{T} t_{m} + c^{m} = R_{bm}^{T} t_{m} + t_{s} + R_{m s} d^{s}

注意到，把旋转变换当作一个变换时，其切换空间满足： $R : A \to B$ , T 为定义在 A 上的线性变换，那么在 B 坐标系下看:

T_{B} = R^{T} TR

v_{c} v_{d} = \frac{d c}{d t} = R_{bm}^{T} \dot{t_{m}} + R_{bm}^{T} S (w_{m}) R_{bm} c^{m} = R_{bm}^{T} \dot{t_{m}} + S (R_{bm}^{T} w_{m}) c^{m} = R_{bm}^{T} \dot{t_{m}} - S (c^{m}) R_{bm}^{T} w_{m} = \frac{dd}{d t} = \dot{t_{s}} + R_{bm}^{T} \dot{t_{m}} + R_{bm}^{T} S (w_{m}) R_{bm} t_{s} + R_{bm}^{T} S (w_{m}) R_{bm} R_{m s} d^{s} + R_{bm}^{T} R_{bm} (S (w_{s m}) R_{m s} d^{s}) = \dot{t_{s}} + R_{bm}^{T} \dot{t_{m}} - S (t_{s}) R_{bm}^{T} w_{m} - S (R_{m s} d^{s}) R_{bm}^{T} w_{m} + (S (w_{s m}) R_{m s} d^{s}) = \dot{t_{s}} + R_{bm}^{T} \dot{t_{m}} - S (t_{s})) R_{bm}^{T} w_{m} - S (R_{m s} d^{s}) R_{bm}^{T} w_{m} - (S (R_{m s} d^{s}) w_{s m})