MPC 控制

MPC 控制

定义

从 PID 控制引入问题

对 PID 控制而言，我们可以将其控制律写为如下形式：

$$u(n)=k_{p}e(n)+k_i\sum _{j=1}^{n}e(j)+k_d(e(n)-e(n-1))$$

可以发现，PID 具有如下的几个问题：

• PID 控制器不具有“前瞻性”：参与计算的量存在当前的 error，上个控制周期的 error，以及之前所有的 error 累计和，但偏偏不存在未来的 error
• PID 属于无模型控制：无模型控制导致对不同物理情形产生不了不同的控制信号，忽略了模型本身的性质

因此我们自然地思考到，需要引入对模型未来的分析，这必然需要得到物理系统的模型，得到了 MPC 控制的思路。

MPC 控制

物理问题

在无限光滑的一维水平直线上有一个质量为 $m$ 的滑块，初始位置与初始速度都是 0，现在需要设计一个控制器，使得在传感器测得滑块位置 $x$ 的基础上，为滑块提供外力 $u$，使其跟随参考点 $x_r$

建立模型

首先建立动力学模型：

$$\ddot{x}=\frac{u}{m}$$

选取状态向量

$$x=\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]$$

，得到状态方程：

$$\dot{x}=Ax+Bu$$

其中，

$$A=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ \frac{1}{m}\end{array}\right]$$

接下来对模型离散化方便计算。

使用前向欧拉法离散状态方程：

$$\begin{array}{rl}\dot{x}& =\frac{x(k+1)-x(k)}{T}=Ax(k)+Bu(k)\\ \Rightarrow x(k+1)& =(I+TA)x(k)+TBu(k)=\bar{A}x(k)+\bar{B}u(k)\end{array}$$

其中，

$$\bar{A}=\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right],\bar{B}=\left[\begin{array}{c}0\\ \frac{T}{m}\end{array}\right]$$

，T 代表控制周期。

预测控制

MPC 方法的一个独特之处就是需要对未来系统状态进行预测，我们记未来 $p$ 个控制周期内预测的系统状态为：

$$X_k=[x(k+1|k{)}^{T}x(k+2|k{)}^T\cdots x(k+p|k{)}^T{]}^T$$

$p$ 称为预测时域，括号中 $k+j|k$ 代表在当前 k 时刻预测 k+j 时刻的系统状态。此外，预测动态系统未来状态时，还需要知道预测时域内的控制量 $U_k$：

$$U_k=[u(k|k{)}^{T}u(k+1|k{)}^T\cdots u(k+p-1|k{)}^T{]}^T$$

$U_k$ 从当前状态的控制量开始，代表了我们需要优化的问题独立变量。

结合离散的控制方程，我们可以得到未来 p 个控制周期的系统状态：

$$\begin{array}{rl}x(k+1|k)& =\bar{A}x(k)+\bar{B}u(k|k)\\ x(k+2|k)& ={\bar{A}}^{2}x(k)+\bar{A}\bar{B}u(k|k)+\bar{B}u(k+1|k)\\ & \cdots \\ x(k+p|k)& ={\bar{A}}^{p}x(k)+\sum _{i=0}^{p-1}{\bar{A}}^{p-1-i}\bar{B}u(k+i|k)\end{array}$$

因此整理为矩阵形式得到：

$$X_k=\Psi x(k)+\Theta U_k$$

其中，

$$\Psi =\left[\begin{array}{c}{\bar{A}}^1\\ {\bar{A}}^2\\ ⋮\\ {\bar{A}}^p\end{array}\right]$$

，

$$\Theta =\left[\begin{array}{cccc}{\bar{A}}^{1-1}\bar{B}& \cdots & 0& 0\\ {\bar{A}}^{2-1}\bar{B}& {\bar{A}}^{2-2}\bar{B}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ {\bar{A}}^{p-1}\bar{B}& {\bar{A}}^{p-2}\bar{B}& \cdots & {\bar{A}}^{p-p}\bar{B}\end{array}\right]$$

.

上面式子中的下三角形式，反映的是时间上的因果关系，即 $k+1$ 时刻的输入对 $k$ 时刻的输出没有影响。

优化

这一小节我们求解预测时域内的控制输出 $U_k$，在求解优化问题之前，首先需要明确优化问题的数学描述。

首先明确我们的控制目标：使得系统的状态跟踪期望的一条轨迹，因此我们定义预测时域内地参考值序列为：

$$R_k=[r(k+1{)}^{T}r(k+2{)}^T\cdots r(k+p{)}^T{]}^T$$

可以发现，为了满足我们的优化目标，必然需要在预测时域内的轨迹信息，这是 MPC 的优越性也是问题所在。

我们希望找到一个最佳的控制量 $U_k$，使得预测时域内的状态向量和参考值越接近越好，那么我们定义这样一个优化函数：

$$J(U_k)=(X_k-R_k{)}^{T}Q(X_k-R_k)+U_k^{T}W{U}_k$$

这一优化问题前面一项代表预测状态向量与参考值之间的累计误差，后面一项代表对控制动作的正则项，减少控制动作。

因此这一控制问题可以描述为如下：

$$\begin{array}{rl}\underset{U_k}{\min }J\left(U_k\right)& \\ s.t.|u(k+i\mid k)|& ⩽u_{\max },i=0,1,2,\cdots ,p-1\end{array}$$

对优化函数进行展开得到：

$$\begin{array}{c}J\left(U_k\right)\\ ={\left(X_k-R_k\right)}^{T}Q\left(X_k-R_k\right)+U_k^{T}W{U}_k\\ =(\stackrel{E}{\overbrace{\Psi x(k)-R_k}}+\Theta U_k{)}^{T}Q\left(\Psi x(k)+\Theta U-R_k\right)+U_k^{T}W{U}_k\\ ={\left(E+\Theta U_k\right)}^{T}Q(E+\Theta U)+U_k^{T}W{U}_k\\ =E^{T}QE+{\left(\Theta U_k\right)}^{T}Q\left(\Theta U_k\right)+2E^{T}Q\left(\Theta U_k\right)+U_k^{T}W{U}_k\\ =U_k^T{\Theta }^{T}Q\Theta U_k+U_k^{T}W{U}_k+2E^{T}Q\Theta U_k+E^{T}QE\\ =U_k^T\left({\Theta }^{T}Q\Theta +W\right)U_k+\left(2E^{T}Q\Theta \right)U_k+E^{T}QE\end{array}$$

其中式子 $E^{T}QE$ 为常数项，因此舍去该项。对于这样二次型优化问题，使用 matlab 提供的优化函数 quadprog，得到：

$$\{\begin{array}{l}H=2\left({\Theta }^{T}Q\Theta +W\right)\\ f^T=2E^{T}Q\Theta \end{array}$$

求解问题为：

$$J(U_k)=\frac{1}{2}{U}_k^{T}H{U}_k+f^T{U}_k$$

仿真

搭建 simulink 模型参考: Simulink 模型

模型跟踪效果为：

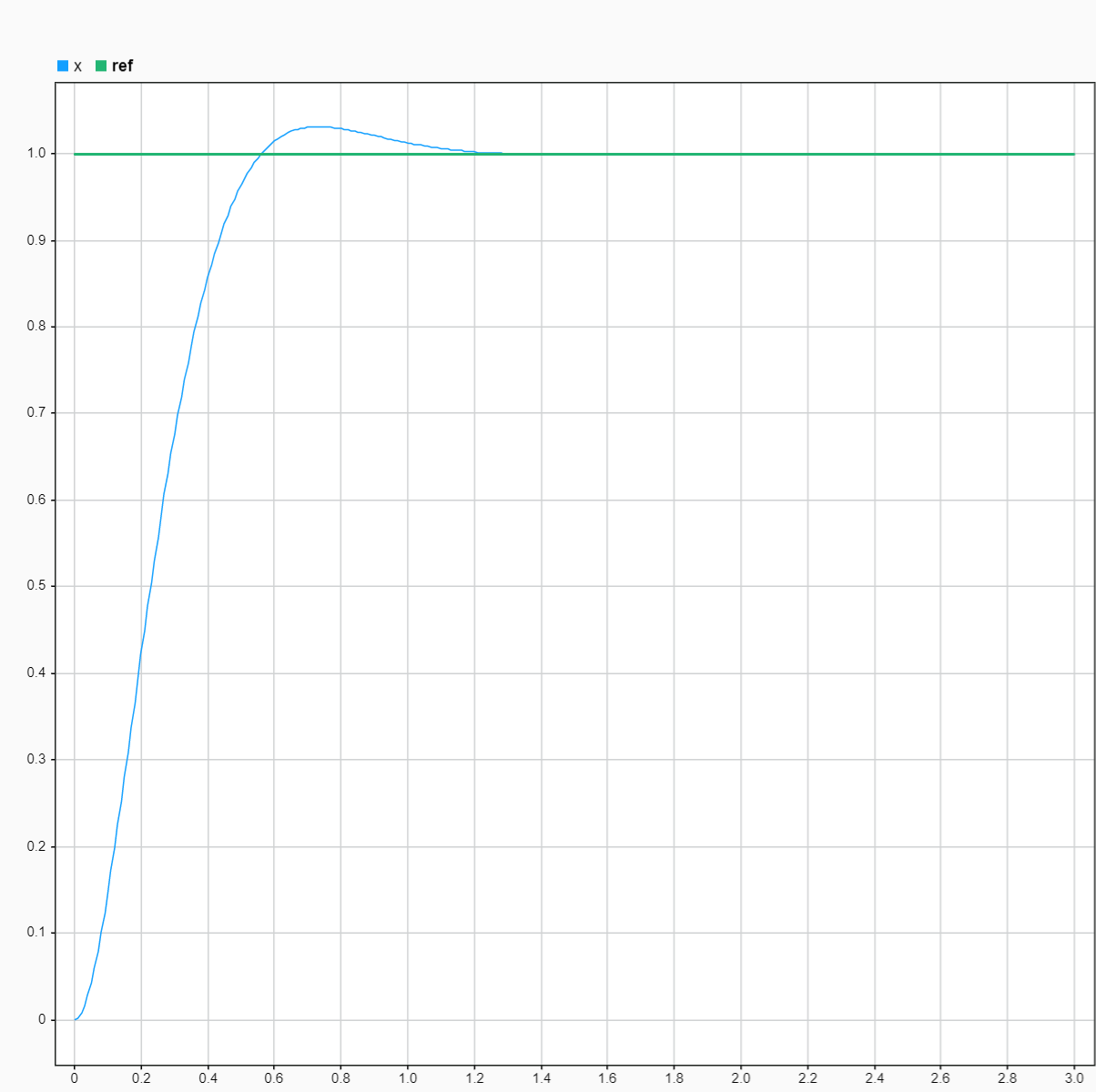
需要注意的是，这里模型跟踪的序列是一个常数序列，因此实现起来较为简单，更复杂情形应该用实际期望轨迹实现。

参考

• 一个模型预测控制（MPC）的简单实现 - 知乎 (zhihu.com)
• Quadratic programming - MATLAB quadprog (mathworks.com)