Chap2 线性系统状态观测器
2022年10月31日
Chap2 线性系统状态观测器
为什么需要状态观测器
那当然是因为全状态反馈控制爽啊!什么东西都知道,可操作空间可太多了!
全状态反馈是一个我们期望的理想条件,但实际过程中我们能够观测到的只有系统的输出,那么我们能否从输出估计出系统的部分状态?如果可以的话,我们就可以直接使用状态观测器+全状态反馈控制完成系统的控制了
系统可观性
实际上,注意到线性系统具有下面的特性:
完全可以通过对可控性的研究来分析可观性的问题
可观性案例
考虑系统:

对其做Jordan分解,利用对偶原理可以发现,第3个状态是不可观测的。对其使用可观性结构分解,可以得到:
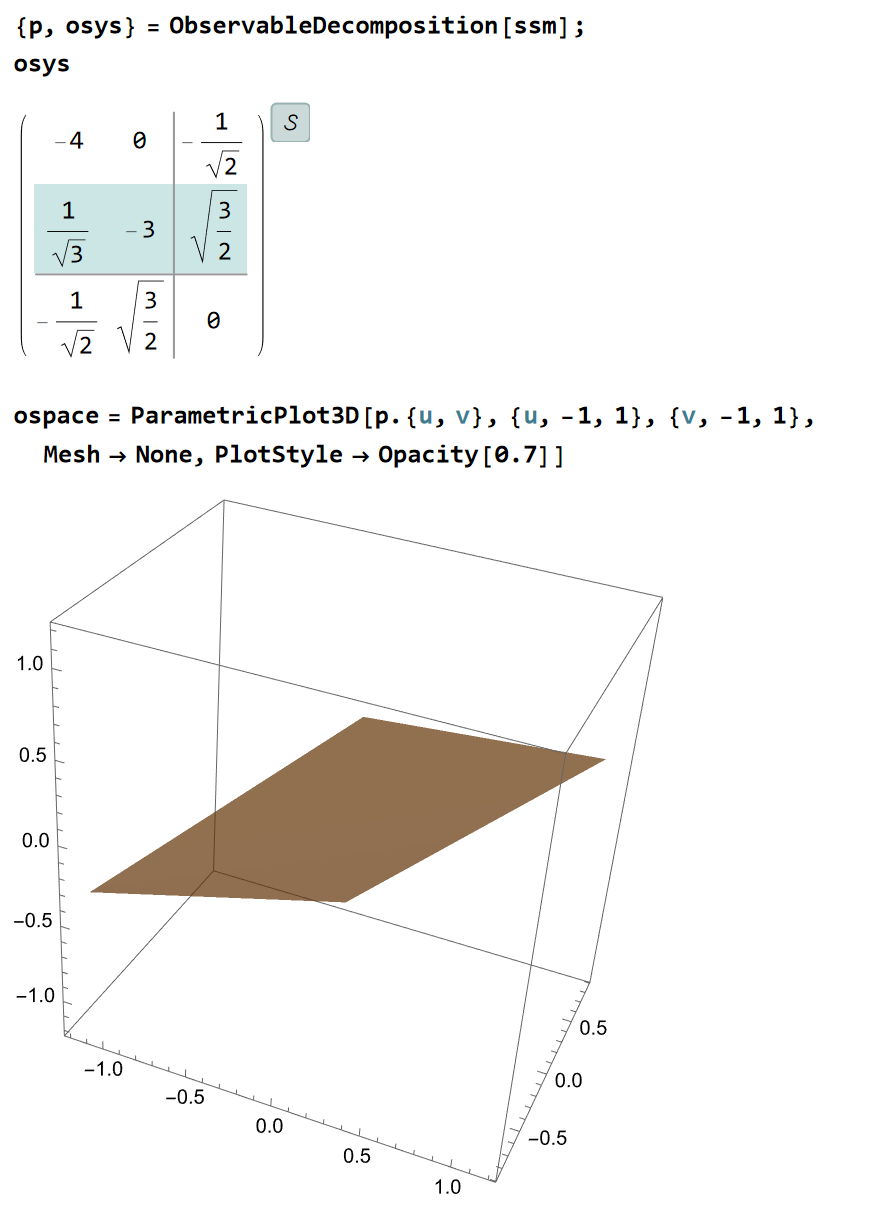
符合我们的分析,其可观状态空间是一个2维平面
如果在可观子空间外选定几组初值,考虑系统的响应:
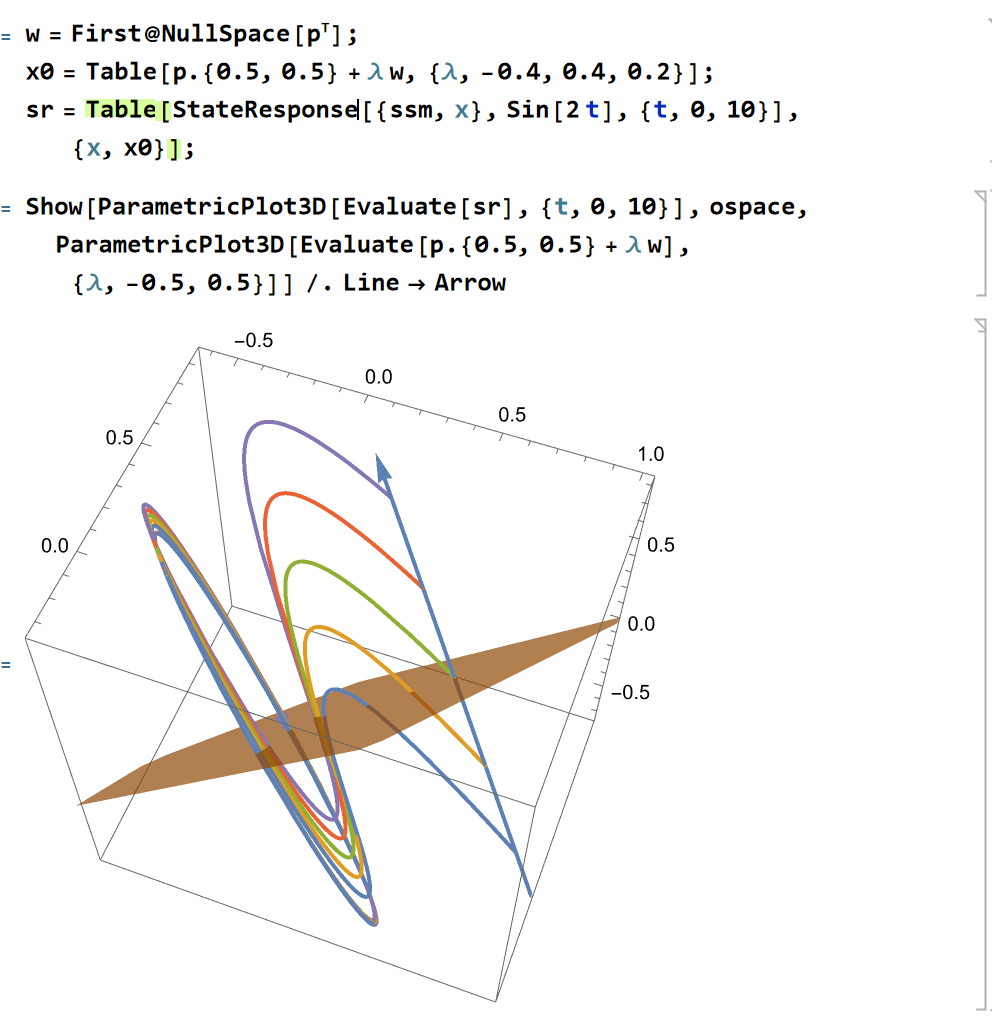
可以发现响应曲线的主法线和切线构成的平面和可观子空间垂直,观察这些不同初始状态下的系统输出:
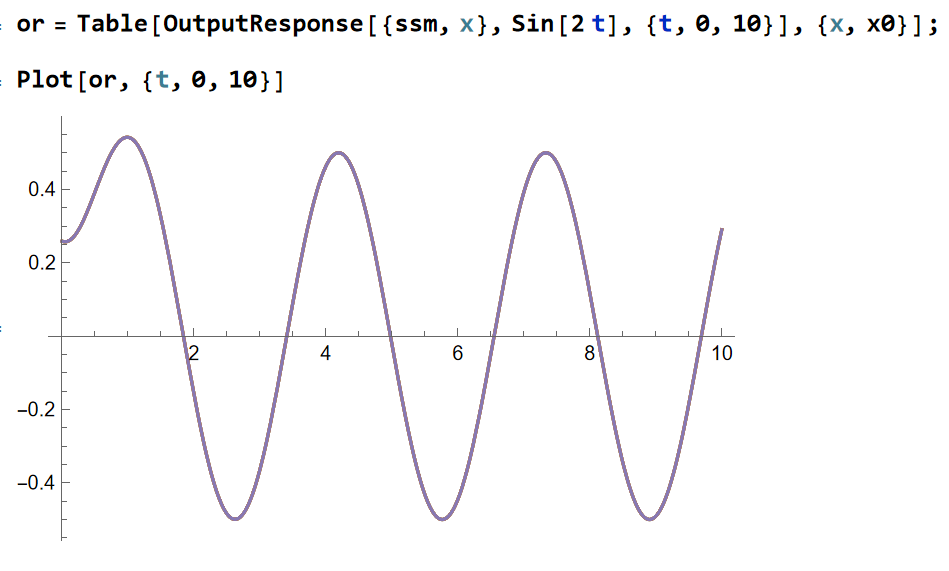
可以发现完全重叠,即确实不能分辨
总之,我们得到的结论就是:
我们观测到的状态是实际状态在可观子空间上的投影
状态观测器
全维观测器
一个直接的思路是做直接反馈:
状态观测器案例
考虑这样一个系统:

可以发现不是完全可观的
对可观性分解后的系统设计观测器极点有:
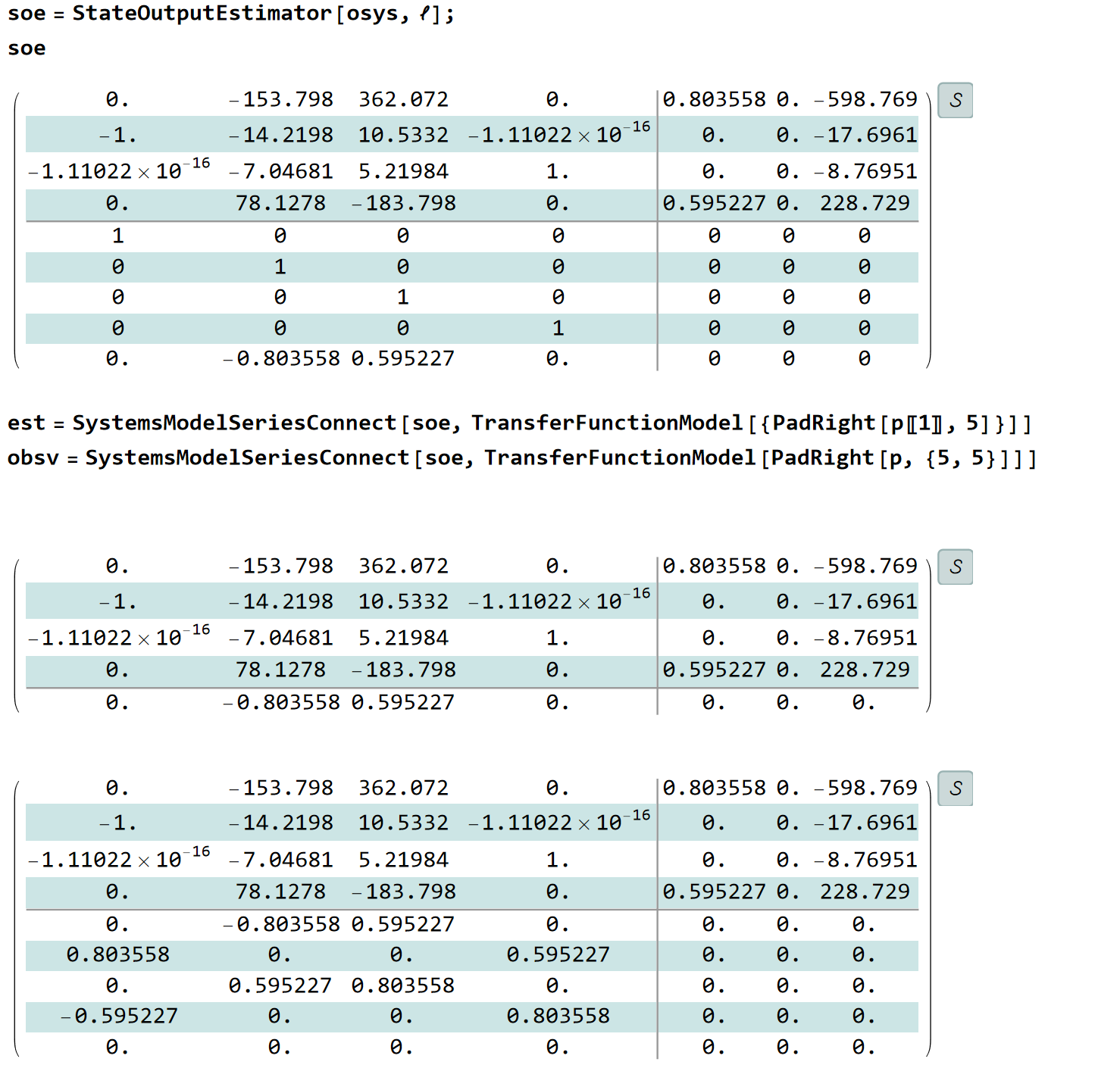
其中obsv是整个系统的完整状态输出,并将输出状态转换为了原始系统的输出
给定一组初值,观察系统的响应有:
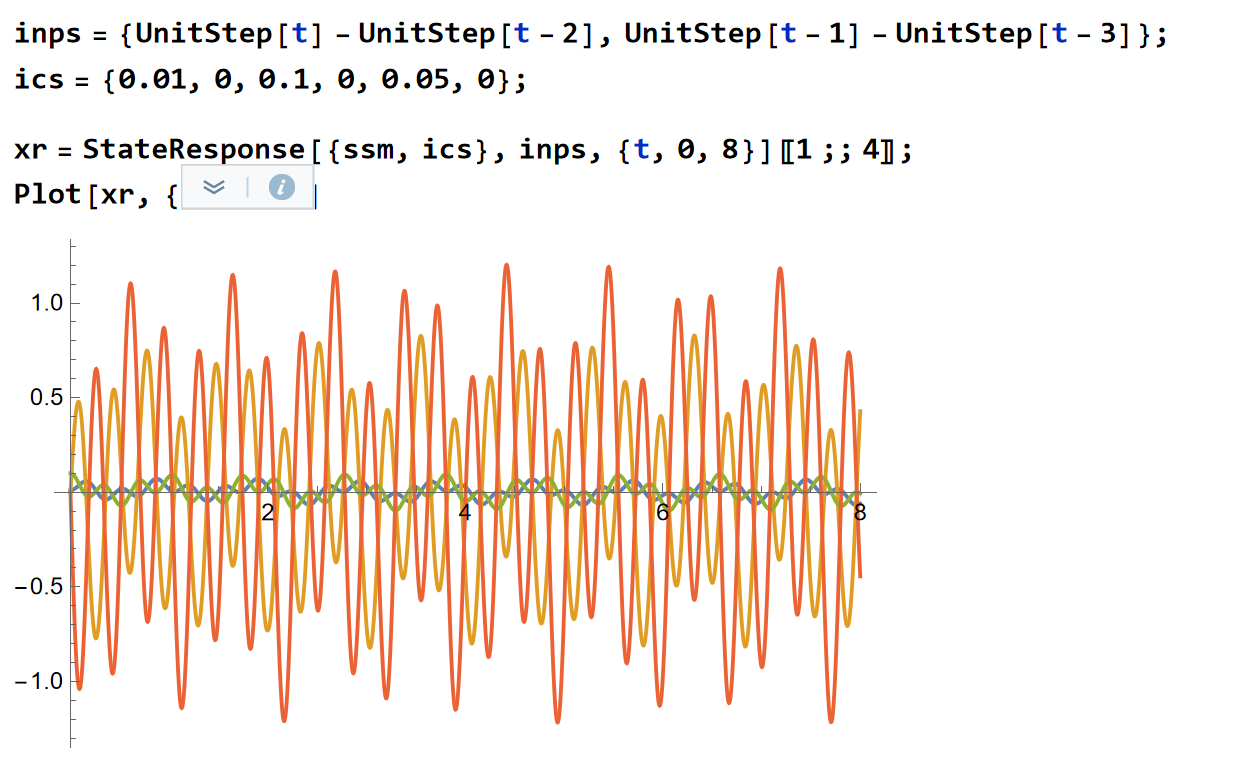
观测器结果:
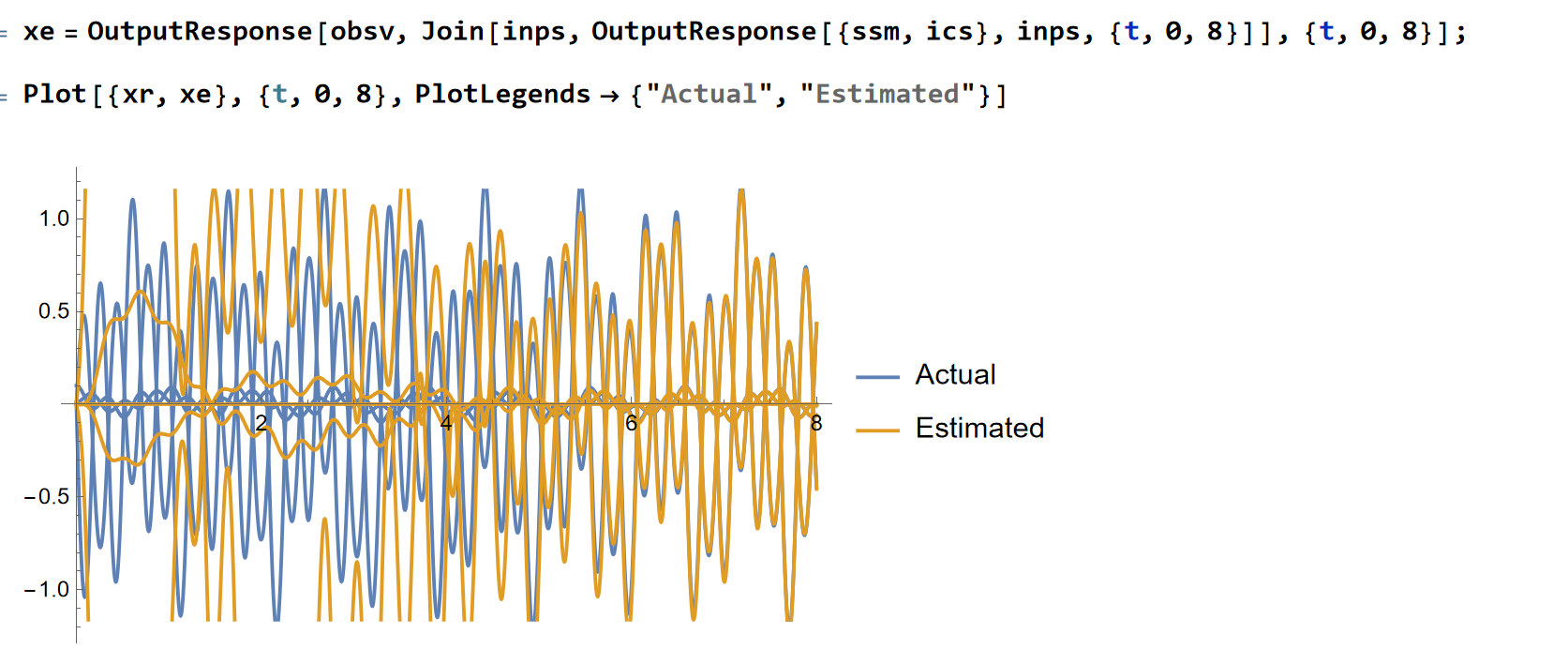
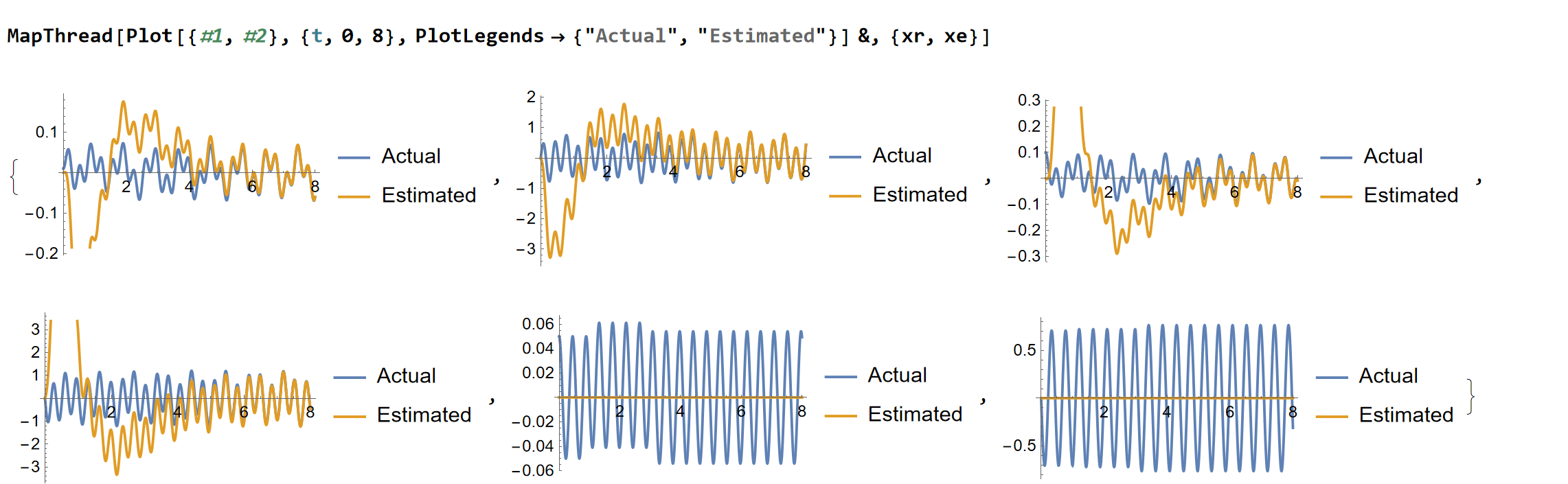
前4个状态可以完全观测,后面2个观测不到
如果修改极点,可以更快地反馈:
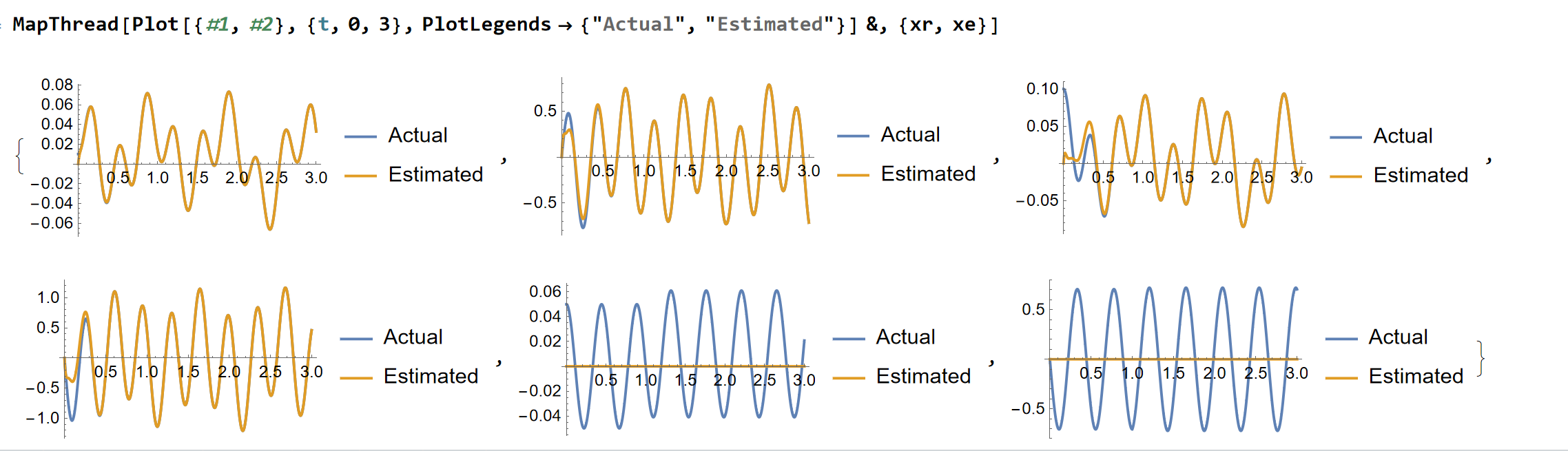
带状态观测器的反馈控制系统
Loading...