Chap3 线性映射

randolf2022年8月9日

library
math
线性代数
从线性映射理解线性代数

math
线性代数应该这样学
linearAlgebra

大约 18 分钟

Chap3 线性映射

前面的线性空间构成了分析的基础，是一个静止的空间。现在来到真正运动的领域——线性映射。Welcome to the true world!

向量空间的线性映射

首先不加引用的直接给出线性映射的定义：

definition

线性映射 定义从V到W的线性映射是具有下面性质的函数 $T : V \to W$

加性：对所有u,v属于V有，T(u+v)=T(u)+T(v)
齐性：对所有 $λ \in F$ 和 $v \in V$ 有 $T (λ v) = λ T (v)$

从这里可以看出，如果 u=v，那么 Tu=Tv。这实际上是一般验证线性映射是否有意义的主要判定方法。

我们记：

definition

$L (V, W)$ 表示从V到W的所有线性映射构成的集合

由于这个概念相当重要，这里给出一些基本的线性映射。

零映射

零映射如下定义： $0 \in L (V, W), s . t .0 v = 0$

恒等映射

恒等映射是某个向量空间上的函数，记为 I。其将每个元素映射为自身，即 $I \in L (V, W), s . t . I v = v$

微分

$D \in L (P (R), P (R)), s . t . D p = p^{'}$

可以发现，我们定义的线性映射集合 L 是一个线性向量空间，其上的代数运算定义为：

$\begin{array}{c} S,T\in \mathcal{L} \left( V,W \right) , \lambda \in F\\ \left( S+T \right) \left( v \right) =Sv+Tv\\ \left( \lambda T \right) \left( v \right) =\lambda \left( Tv \right)\\ \end{array}

有别于基本的向量空间运算，对于线性映射我们也可以定义新的运算，即线性映射的乘积。

definition

线性映射的复合/乘积

T \in L (U, V), S \in L (V, W) define ST \in L (U, W) ST (u) = S (T (u))

对于这样的线性映射乘积运算，可以验证其满足这样的一些性质：

结合性： $(T_{1} T_{2}) T_{3} = T_{1} (T_{2} T_{3})$
单位元： $T I = I T = T, T \in L (V, W)$
分配性质： $(S_{1} + S_{2}) T = S_{1} T + S_{2} T S (T_{1} + T_{2}) = S T_{1} + S T_{2}$

线性映射的性质

对于一个线性映射，自然地可以考虑这样的两个问题：

他能将那些向量映射为 0？
他能映射到那些向量？

这分别对应了两个子空间：零空间和值域

definition

零空间

T \in L (V, W), null T = {v \in V ∣ T v = 0}

值域

range T = {T v ∣ v \in V}

容易证明零空间和值域是一个子空间。

注意，由于线性映射是一个映射，因此也可以定义单射和满射的思路。

definition

单射：Tu=Tv时必有u=v，称T是单射
满射：T:V->W的值域=W

不难发现，单射性等价于零空间为 {0}，而满射就是值域等于 W

引入了值域和零空间，这将线性映射和其作用的向量空间联系起来，我们自然会考虑这两者之间存在什么联系，这引出了一个非常重要的定理：

lemma

线性映射基本定理 假设V是有限维的， $T \in L (V, W)$ ，那么有：

dim V = dim null T + dim range T

根据上面定理，一个直观的结果就是：

到更小维数向量空间的线性映射不是单的
到更大维数向量空间的线性映射不是满的

表示线性映射

注意到，我们现在描述线性映射还是使用一种规则进行描述，还不存在与之对应的数字实体。这里我们将引入前面介绍的从向量组构成线性空间的基来对线性映射进行描述。

基本的思路是这样的：注意到，由于 T:V->W 是线性的，因此 Tvi 就确定了 T 在 V 上的所有向量的值，因此使用 W 的基就可以有效的记录这些值，从而描述一个线性映射。

definition

矩阵设m,n都是正整数，mxn矩阵A是由F的元素构成的m行n列的阵列：

A = ⎝ ⎛ A_{1, 1} ⋮ A_{m, 1} \dots \dots A_{1, n} ⋮ A_{m, n} ⎠ ⎞

其中Aj,k代表A的j行k列的元素

根据上面的思想，我们可以定义线性映射的矩阵：

definition

线性映射的矩阵M(T)

T \in L (V, W) v_{i} 是 V 的基 w_{i} 是 W 的基 M (T) = A T v_{k} = A_{1, k} w_{1} + \dots + A_{m, k} w_{m}

由于之前定义了线性映射之间的运算关系，自然会考虑其产生的矩阵之间的定义关系。在相同的基下，显然可以得到和线性映射相同的运算结构，即 M(S+T)=M(S)+M(T)，矩阵加法为对应元素相加。

比较复杂的是矩阵乘法，对应于线性映射的乘法。定义如下：

definition

矩阵乘法 A:mxn矩阵，C:nxp矩阵，AC定义为mxp矩阵，有：

(A C)_{j, k} = r \sum A_{j, r} C_{r, k}

可以验证，线性映射对应的矩阵之间的乘法和线性映射的乘法具有相同的结构： M(ST)=M(S)M(T)

可以说，线性映射和其对应的矩阵有一些深层次的联系，后面会提到，这一联系也是一个线性映射，而且具有很多很好地性质，其表明了在指定基的情况下，线性映射和矩阵是一个东西！

关于矩阵的一些理解可以参考 liShenQiDeJuZhen2020 和 liShenQiDeJuZhen22020

特殊的线性映射

可逆线性映射

首先定义线性映射的可逆和逆。

definition

线性映射 $T \in L (V, W)$ 被称为可逆的，如果存在线性映射 $S \in L (W, V)$ 使得ST满足V上的恒等映射且TS等于W上的恒等映射
满足ST=I和TS=I的线性映射 $S \in L (W, V)$ 称为T的逆

不难证明，逆是唯一的，因此我们可以给其一个记号： $T^{- 1}$

可逆性的定义比较好理解，就是字面意义的“可逆”。从其作用效果上来看，可以发现，一个线性映射若是可逆的，那么其 可逆性实际上等价于单性和满性

可逆的线性映射是一类特殊的线性映射，它表明线性映射的效果是可以被逆转的，因此作用前后的两个空间必然有某种联系（注意单性和满性保证了两空间至少是维数相等的），这个联系被称为同构

definition

同构

同构就是可逆的线性映射
若两个向量空间存在一个同构，则称这两个向量空间是同构的

上面提到，可逆性等价于单性和满性，自然蕴含了两个空间是相同维数的。这里我们给出，F 上两个 有限维向量空间 同构当且仅当其维数相同

上面的说法表明，每个有限维向量空间都同构于 $F^{n}$ ，这立马减少了我们研究问题外表上的复杂性——所有的空间都是按照维数排列的。前面介绍矩阵的时候就隐含了矩阵和其线性映射是有关系的，这里说明他们（矩阵空间和线性映射空间）之间其实是同构的。

既然线性映射和矩阵是同构的，我们可以将线性映射的所有操作搬移到矩阵运算上（注意存在矩阵就表明已经存在一组基了）。

一个直观的事实是：M(Tv)=M(T)M(v)，这就是我们前面说的同构的威力，将定义在规则层面的线性映射转换到数值运算层面，而不改变其含义。

算子

另一种比较特殊的线性映射关注的是这样：向量空间到自身的线性映射。定义如下：

definition

算子

向量空间到自身的线性映射称为算子
$L (V) = L (V, V)$

考虑前面介绍的线性映射的性质，我们来考察算子的性质。前面介绍，若一个线性映射既单又满那么其可逆；我们想考虑，对算子，什么时候才可逆？

lemma

在有限维的情形，单性等价于满性 假设V是有限维的， $T \in L (V)$ ，下面陈述等价

T是可逆的
T是单的
T是满的

可以注意到，使用线性映射基本定理可以直接得到结论。

由于这个定力很重要，这里附加一个例子：

Pasted image 20220309145224

一个更酷炫的习题如下：

Pasted image 20220309145309 Pasted image 20220309145318

线性映射生成新的向量空间

在分析完基本的线性映射的特征后，我们可以使用线性映射的方法得到一些新的向量空间

首先定义向量空间的乘法 (在向量空间构成的集合上|由于同构的性质这是可以办到的)

definition

设V1,V2,...,Vm是F上的向量空间，那么定义：

$V_{1} \times \dots \times V_{m} = {(v_{1}, \dots, v_{m}) ∣ v_{1} \in V_{1}, \dots, v_{m} \in V_{m}}$
$V_{1} \times \dots \times V_{m}$ 是一个向量空间
$V_{1} \times \dots \times V_{m}$ 上的加法为： $(u_{1}, \dots, u_{m}) + (v_{1}, \dots, v_{m}) = (u_{1} + v_{1}, \dots, u_{m} + v_{m})$
$V_{1} \times \dots \times V_{m}$ 上的标量乘法为： $λ (u_{1}, \dots, u_{m}) = (λ u_{1}, \dots, λ u_{m})$

Pasted image 20220309150131

容易证明，向量空间积的维数等于维数的和。

我们注意到，空间的积和空间的和之间似乎有些联系，只需要将乘法转换为加法就可以，事实上也的确如此。前面线性映射的性质告诉我们，研究空间之间的关系，实际可以从线性映射入手，因此得到下面的结论：

definition

积与直和 设U1,...,Um均为V的子空间。线性映射 $Γ : U_{1} \times \dots \times U_{m} \to U_{1} + \dots + U_{m}$ ，定义有 $Γ (u_{1}, \dots, u_{m}) = u_{1} + \dots + u_{m}$ ，从而 $U_{1} + \dots + U_{m}$ 是直和当且仅当 $Γ$ 是单射(事实上由于 $U_{1} + \dots + U_{m}$ 的定义， $Γ$ 一定是满的，因此可以将单射转换为可逆) 从而表明： $dim (U_{1} + \dots + U_{m}) = dim U_{1} + \dots + dim U_{m}$ 等价于直和

定义了积空间，自然可以考虑商空间。

积空间定义的结果是子空间的积基本上同构于直和，其维度上满足加法。自然地可以猜测商空间的情况应该是减少相应的维数的运算。

首先定义向量和子空间的和：

definition

设v in V，U是V的子空间，则v+U是V的子集，定义为：

v + U = {v + u ∣ u \in U}

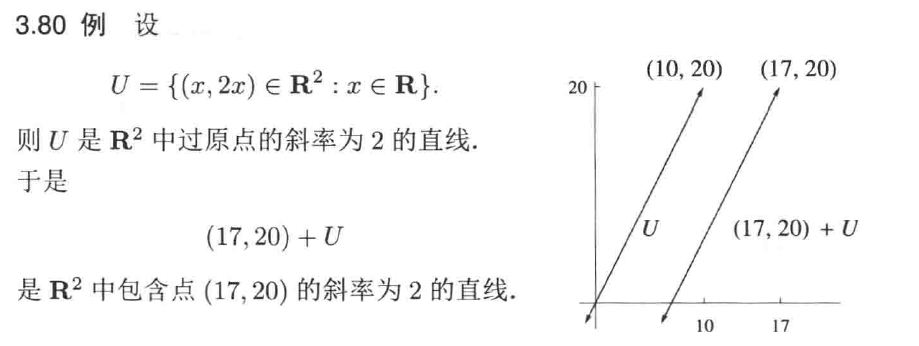
Pasted image 20220309151639

进一步可以定义 仿射子集 和平行的概念

definition

V的仿射子集是V的形如v+U的子集，其中v in V，U是V的子空间
对于v in V和V的子空间U，称仿射子集v+U平行于U

平行的仿射子集：例如上面介绍的，R2 中所有斜率为 2 的直线均平行于 U

有了这些定义，我们可以定义商空间的概念：

商空间

definition

假设U是V的子空间，定义商空间V/U是指V的所有平行于U的仿射子集的集合

V / U = {v + U ∣ v \in V}

现在考察这个商空间是否是一个向量空间：

为了验证这一点，下面给定这样几个命题：

lemma

平行于U的两个仿射子集或相等或不相交 设U是V的子空间，v,w in V，那么下面的陈述等价：

v-w in U
v+U=w+U
(v+U)∩(w+U)≠空集

为了验证商空间是不是向量空间，我们定义商空间上的加法和标量乘法：

definition

假设U是V的子空间，则V/U的加法和标量乘法定义为：

(v+U)+(w+U)=(v+w)+U
λ(v+U)= λv+U

在这里定义的加法和标量乘法下，商空间是一个向量空间。

类似上面积空间导出了一个映射，我们可以定义一个商映射来分析商空间的基本性质——比如维数。

definition

商映射 设U是V的子空间，商映射🥧是下面定义的线性映射：🥧:V→V/U，其规则为： 🥧(v) = v+U

容易验证，🥧确实是一个线性映射，它满足线性映射的加性和齐性向量空间的线性映射

从而，根据线性映射基本定理，可以量化商空间的维数：

只需要注意：null 🥧=U，range 🥧=V/U，从而： dim V/U = dim V - dim U

上面商空间是一个依赖于 V 和其子空间 U 的向量空间，因此可以考虑其这样的一个实例：对 V 上的每个线性映射 T，其诱导了一个线性映射 $\hat{T}$ ，满足：

设 $T \in L (V, W)$ ，定义 $\hat{T} : V / (n u llT) \to W$ ：

\hat{T} (v + n u llT) = T v

这个也是一个线性映射，容易证明。但为啥要提出这样一个线性映射呢？是为了做一个演示的例子。由于线性映射基本定理，dim V = dim null(T) + dim range(T)，从而有：dim V/nullT = dimV - dim null(T) = dim range(T)，这意味着 V/nullT 和 range T 同构。这个线性映射就是一个同构的例子。

只需要验证这是一个单射就行了，而其显然是满射，从而构造了一个同构关系，也是验证了线性映射基本定理。

线性泛函和对偶

在前面特殊的线性映射中介绍了一些具有特殊性质的线性映射，这里可以再增加一例：映到标量域 F 的线性映射，也称为 线性泛函，是 L(V,F) 中的元素。

Pasted image 20220309191409

对这样的线性映射，我们可以考虑其组成的向量空间（前面应该提过线性映射构成的这类空间也是向量空间），定义其为 对偶空间

definition

对偶空间 V上所有线性泛函构成的向量空间称为V的对偶空间，记为V'，即V'=L(V,F)

注意到，dim V' = dim L(V,F) = dimV×dimF=dimV，从而表明对偶空间和原始空间是同构的！这就很有意思了。我们知道，同构的空间是很相似的，具体来说，只要找到了对应的量空间下的基并将其一一对应，我们可以将空间完全转换到新的空间下。这引导我们考虑对偶空间下的基：对偶基

definition

对偶基 假设v1,...,vn是V上的基，那么v1,...vn的对偶基是V'中的元素组 $ψ_{1}, \dots, ψ_{n}$ ，其中每个 $ψ_{j}$ 都是V上的线性泛函，使得：

ψ_{j} (v_{k}) = {10 当 k = j 当 k \neq = j

容易证明，对偶基的确是一组 V' 上的基。

我们发现对偶空间和原空间具有相同的维数，这表明他们之间可以相互转化。前面我们考虑了线性映射 L(V,W)，自然地可以考虑在对偶空间下的线性映射的关系，即研究 L(V',W') 和 L(W',V')，则引入了 对偶映射 的概念

definition

对偶映射 若T∈L(V,W)，则T的对偶映射定义为T'∈L(W',V')：满足对ψ∈W'，有：

T^{'} (ψ) = ψ \circ T

注意，这确实是一个线性映射，将 W 上的线性泛函ψ映射到了 V 上的线性泛函。相对来说比较绕，举例如下： Pasted image 20220310154856

lemma

对偶映射的代数性质

对所有S，T∈L(V,W)，有(S+T)'=S'+T'
对所有λ∈F和所有S∈L(V,W)，有(λT)'=λT'
对所有T∈L(U,V)和所有S∈L(V,W)，有(ST)'=T'S'

上面的结果表明这确实是一个线性映射。说明了这是一个线性映射后，和上面研究思路一样，开始考虑线性映射构成的集合上的关系，也就是看他是不是可以构成一个向量空间。研究一个线性映射的性质无非就是看其零空间、值域的特性，从而我们引入下面的定义：

definition

零化子 对于V的子空间U，U的零化子( $U^{0}$ )定义为

U^{0} = {ψ \in V^{'} ∣ 对所有 u \in U 都有 ψ (u) = 0}

对于 V 的子空间 U，零化子 $U^{0}$ 是对偶空间 V' 的子集，因此其依赖于包含 U 的向量空间 V，但由于 V 一般是上下文自明的，因此不做特殊说明。

容易证明，零化子是一个子空间，我们来研究其维数：

lemma

假设V是有限维的，U是V的子空间，则：

dim U + dim U^{0} = dim V

定义这样一个映射 i∈L(U,V)，满足：对 u∈U 有 i(u)=u，这是一个自然地映射。考虑其对偶映射 i'∈L(V',U')。注意到 $null i^{'} = U^{0}$ ，而 $dim V^{'} = dim V$ 。对 i' 使用线性映射基本定理有

dim range i^{'} + dim null i^{'} = dim V^{'} \Rightarrow dim range i^{'} + dim U^{0} = dim V

假定ψ∈U'，那么可以将其扩张为 V 上的线性泛函φ，从而根据 i' 定义有：

i^{'} ϕ = ϕ \circ i = ψ

从而表明ψ∈rangei'，进而有 rangei'=U'，故：

dimrange i^{'} + dim U^{0} = dim V \Rightarrow dim U + dim U^{0} = dim V

这里的结果暗示我们下面两个空间是同构的：

$U^{0}$ ：U 的零化子，属于 V' 层面，成员是 V 上的线性泛函
V/U：U 的商空间，属于 V 层面 (虽然不是 V 子集)，成员是一簇平行的仿射集

在零化子的前置知识下，可以考虑对偶映射的值域和零空间的性质：

lemma

T'的零空间 假设V和W都是有限维，T∈L(V,W)，则：

$null T^{'} = (range T)^{0}$
$dimnull T^{'} = dimnull T + dim W - dim V$

容易证明第一条性质，第二条使用线性映射基本定理可以得到。这里结果表明，如果 T 是一个 V 上的算子，那么 T' 和 T 的零空间同构，事实上其是 T 值域的零化子

此外，还给了我们一个看线性映射的新角度，即证明 T 是满的等价于 T' 是单的

lemma

T'的值域 假设V和W都是有限维，T∈L(V,W)，则：

$range T^{'} = (null T)^{0}$
$dimrange T^{'} = dimrange T$

可以发现其值域和零空间是 T 对应的零化子。类似上面结论有：T 是单的等价于 T' 是满的

这表明 T 和 T' 是很相似的，他们互“共享”零空间和值域，构成的向量空间具有相同的维数。下面根据表示线性映射介绍的矩阵来数值上看下两个线性映射的关系

我们可以定义一个矩阵空间上的新运算，称奇为转置

definition

转置矩阵A的转置(记为 $A^{T}$ )是通过互换A的行和列所得到的矩阵，即：

(A^{T})_{k, j} = A_{j, k}

容易根据定义证明，矩阵具有这样的性质： $(A C)^{T} = C^{T} A^{T}$

我们证明，假定 V 有基 v1,...,vn 及 V' 的对偶基ψ1,...,ψn，并假定有 W 的基 w1,...,wn 及 W' 的对偶基φ1,...φn，矩阵 M(T) 按照 V 和 W 的上述基计算，M(T') 是按照 W' 和 V' 的上述基计算。从而有：

lemma

T'的矩阵是T矩阵的转置 设T∈L(V,W)，则

M (T^{'}) = (M (T))^{T}

我们成功表明了线性映射和其对偶映射存在紧密的联系，下面来看看这样的联系可以带来什么样的结果。

我们对矩阵进行分析，定义矩阵的秩为：

definition

矩阵的秩 假设A是元素属于F的mxn矩阵

A的行秩是A的诸行在 $F^{1, n}$ 中的张成空间的维数
A的列秩是A的诸列在 $F^{m, 1}$ 中的张成空间的维数

容易看出，rangeT 的维数等于 M(T) 的列秩，从而根据我们上面对偶映射的性质，对偶映射的值域和原映射的值域维数相同，从而有 行秩等于列秩，也就是说可以统一起来称矩阵的秩，一般使用列秩，因为其是直接的 T 的值域

Chap3 线性映射

# Chap3 线性映射

# Chap3 线性映射

# 向量空间的线性映射

# 线性映射的性质

# 表示线性映射

# 特殊的线性映射

# 可逆线性映射

# 算子

# 线性映射生成新的向量空间

# 商空间

# 线性泛函和对偶

Chap3 线性映射

Chap3 线性映射

向量空间的线性映射

线性映射的性质

表示线性映射

特殊的线性映射

可逆线性映射

算子

线性映射生成新的向量空间

商空间

线性泛函和对偶