Chap10 迹和行列式

Chap10 迹和行列式

迹：算子和矩阵之间的联系

definition

算子的迹 设T∈L(V)

• 若F=C，则T的迹等于T的按照重数重复的全体本征值之和
• 若F=R，则T的迹等于$T_C$的按照重数重复的全体本征值之和 T的迹记为$\mathrm{trace}T$

显然，$\mathrm{trace}T$ 等于 T 的特征多项式 $z^{n-1}$ 的系数的相反数

下面可以证明，算子的迹等于其矩阵的迹，其中矩阵的迹等于矩阵主对角线元素之和

lemma

算子的迹等于其矩阵的迹 若T∈L(V)，则$\mathrm{trace}T=\mathrm{trace}M\left(T\right)$

迹具有下面的性质：迹是可加的，即 $\mathrm{trace}\left(S+T\right)=\mathrm{trace}S+\mathrm{trace}T$

行列式

行列式有下面的特性：

lemma

T的特征多项式等于$\det \left(zI-T\right)$ 设T∈L(V)，则T的特征多项式等于$\det \left(zI-T\right)$

关于矩阵的行列式，有：

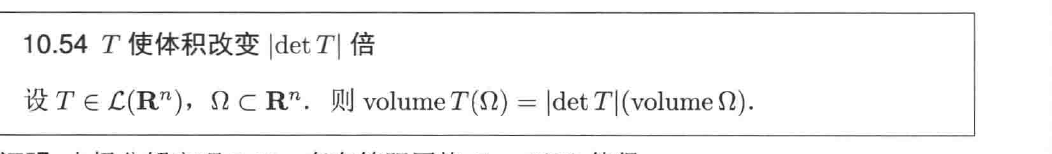
一个 det 的例子有：

一个计算实例为：