Chap2 拓扑空间
Chap2 拓扑空间
拓扑空间定义和性质
什么事拓扑
note
我们引入拓扑空间(topology space)的想法是:
一个几何上的拓扑给我们提供了一个具有下面2个性质的最弱的结构:
- 集合中点集的收敛(convergence of sequences to points in a set)
- 两个集合之间的映射的连续性(continuity of maps between 2 sets)
^note-why-topo
拓扑空间
集合 M 上定义一个拓扑 (topology) ,为: 且:
这个配对 就是我们所说的拓扑空间 (topology space).
^def-topo
remark
注意正如前面定义 N, Z, R 这些数域使用集合的角度来定义,这里的拓扑也是一个集合的角度来定义的。实际上我们所说的很多结构,都是一些具有特殊性质的集合
remark
除非 , 一般来说对一个集合M我们有很多种选取拓扑的方法:
| 集合M的势 | 拓扑数量 |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 29 |
| 4 | 355 |
| 5 | 6942 |
| 6 | 209527 |
| 7 | 9535241 |
remark
- 假定 ,那么我们可以选取 就是一个可行的拓扑
- 假定 M 是一个集合,那么我们可以选取拓扑 是一个合理的拓扑
- 按照这样构造的拓扑被称为 chaotic topology,显然可以应用在任何集合上
- 假定 M 是一个集合,那么我们可以选取拓扑
- 这样构造的拓扑显然是合适的,我们称其为discrete topology
- 如果 是集合M上的2个拓扑,如果 ,那么我们称 是比 更弱的(coarser/weaker topology). 等价的,我们称 是更强的(finer/stronger topology)
- 显然chaotic topology 是最弱的,discrete topology是最强的
- 后面展开讲拓扑空间性质的时候会明白为什么说最强/最弱
^remark-chaotic-discrete-topo
拓扑空间性质展开
集合开集
开集
如果 是一个拓扑空间,那么可以定义 M 的子集 S 是 开的(open with respect to ): 集合 ;反过来,子集 S 是闭的 (with respect to ),如果 (补集是开集)
^def-open-set
remark
很容易误解的一点是,开集和闭集不是互斥的,一个集合可以是开集也可以是闭集。此外,根据我们的定义,开集是依赖于拓扑的,相同的子集在不同的拓扑下可能会在开集和闭集之间变换
example
- 是一个拓扑空间, 是开的因为 。但是 也是闭的因为 。对 M 也是一样的
- 假定 ,那么我们可以选取 ,那么 是开的,但不是闭的, 是既不是开的也不是闭的
标准拓扑
为了将拓扑更容易地应用到技术上,即定义在 上的 标准拓扑 (standard topology),其中 为:
我们给出一些辅助的定义:
开球
对 且 ,我们定义在点 x 处的 开球(open ball):
其中 而且 其中
^def-open-ball
remark
上面的 实际上是 2 范数,但考虑到范数的定义依赖于集合上的 线性空间结构,而我们还没有定义。不过我们这套定义的思路可以延展到不同的范数上去,这些范数导出的开球导出的标准拓扑具有相同的结构
标准拓扑
上的标准拓扑 被定义为:
^def-standard-topo
直观上来看,我们定义的标准拓扑是说其中任取一个点,这个点周围可以构造一个开球,这个开球也在拓扑范围中。我们将证明,定义的标准拓扑 和 构成的 是一个拓扑空间:
theorem

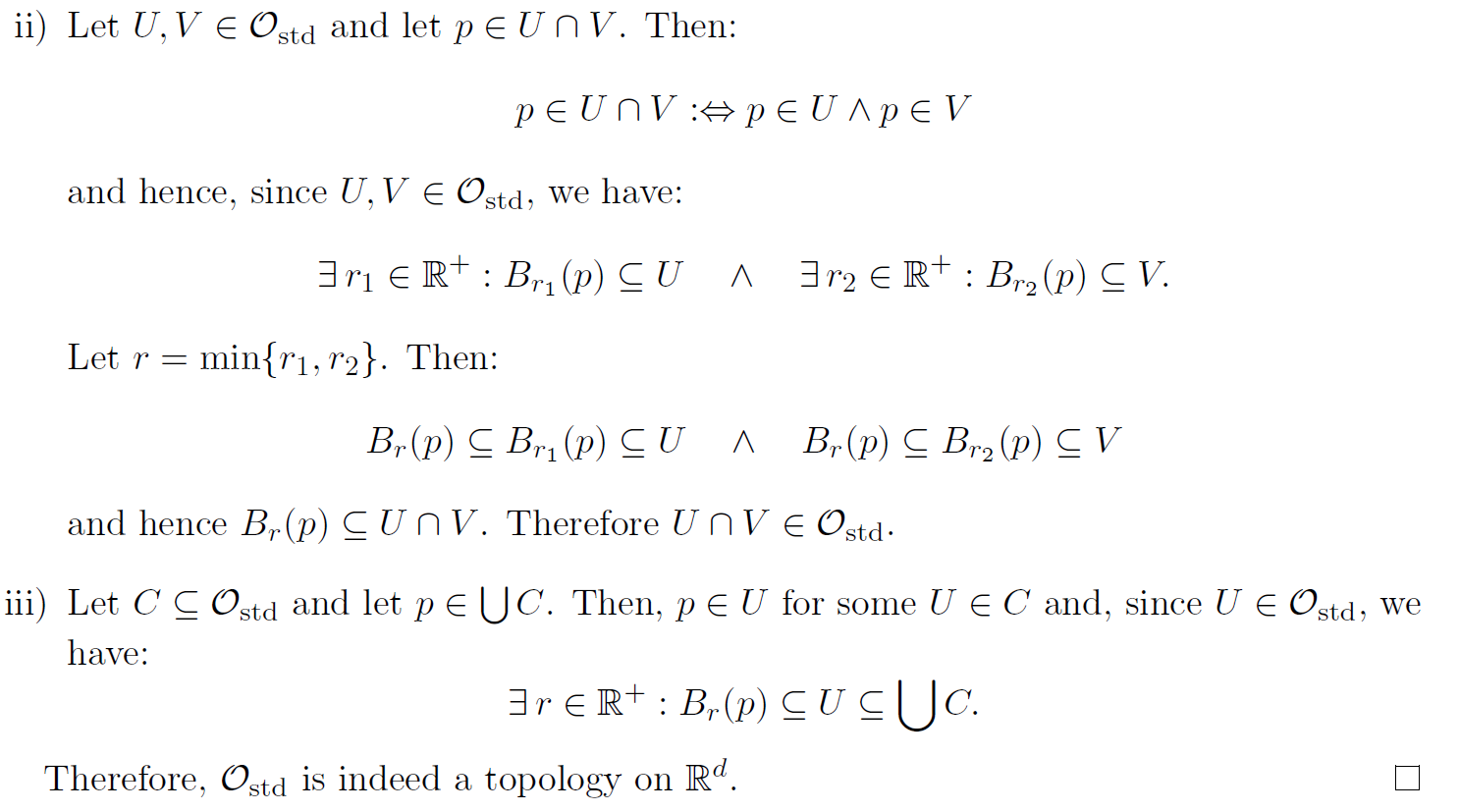
从现有拓扑构造新的拓扑
Induced Topology
假设我们已经有了一个拓扑 ,集合 有子集 ,那么我们定义:
^def-sub-top
可以证明,这是一个在 上的拓扑,被称为**induced(subset) topology **
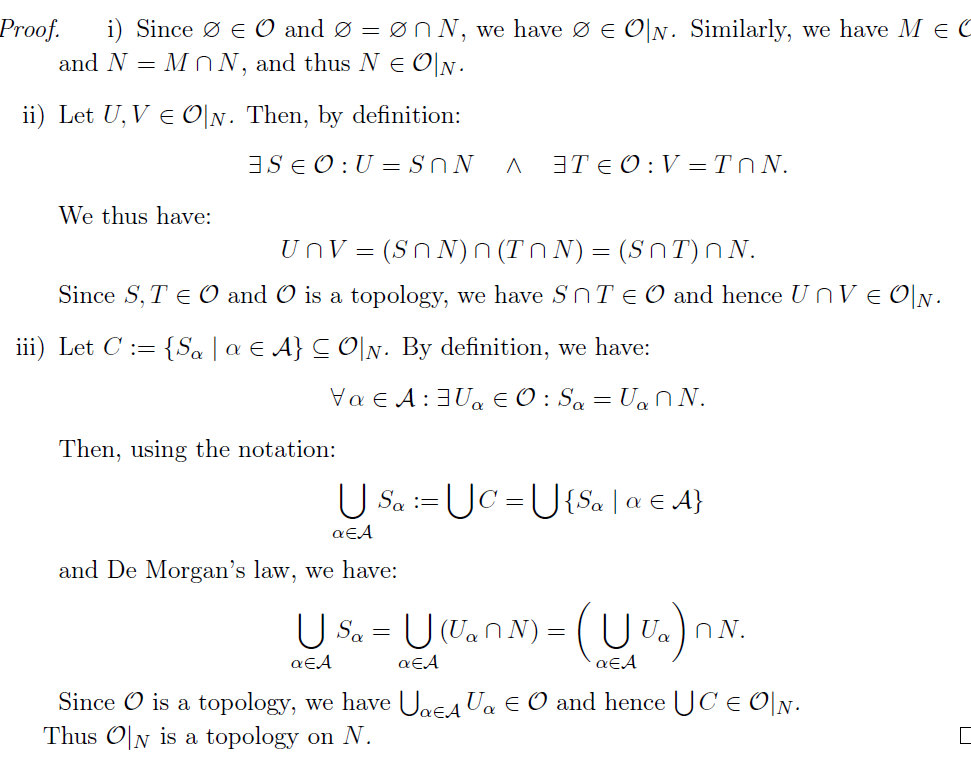
Quotient Topology
quotient topology
假设我们已经有了一个拓扑 , 是 M 上的一个等价关系,那么在 M 上可以定义等价类/商集:
对商集我们按照 Induced Topology 类似的思路,装备拓扑:
针对上式的一个等价定义是:
考虑映射
新拓扑可以表示为:
^def-quotient-topo
这里的 quotient topology 定义确实看起来比较奇怪,可以参考 [2] 进行解释:
想象我们有一个 上的集合 ,其继承了 R 上的标准拓扑。在这个集合上考虑一个简单的等价关系 ,其将这个集合划分为两类,一类为 2 点 .
note
literally 就只有这 2 个点,代表着这个拓扑空间 M 上的起点和终点,这个说法是想象我们是住在这个空间 M 上的生物,所谓的内蕴几何
另一类是其余的 。显然这构成了一个等价类。考虑在这个商集上定义一个映射,可以将其 一一映射 到圆环上:
这显然是一个定义在该商集上的一一映射 (毕竟一共 2 个元素),而对于这个商集来说,确实就和圆环构成了一一映射,表示这两个空间是同构的。
现在来看我们对 quotient topology 的定义。由于一共只有 2 个元素,首先对 进行检验,有:
这里的 代表的是集合 M 的子集,确实是一个开集嘛,因此
对于元素 进行检验:
因为在 R 上不存在一个开集使得其交 为其两端点,因此这表示这个 quotient topology 为:
一共这 3 个元素。
如果脱离我们 " 生活在 M 上的视角 ",将其放到圆环的角度来看。由于存在一一映射 h,表明这个商集和圆环是同构的,从而其上的拓扑可以完全一样的延展到圆环上。这样延展过去的拓扑是:
这里的 的意思是排除了 点的圆环。
如果将圆环上的拓扑看成从 上的标准拓扑继承下来的,那么其拓扑为圆环上所有圆弧的集合,显然包含了上面的拓扑,这也体现了视角的不同。
corollary
可以将商空间和quotient topology看成一个弯折的过程,在上面的例子中就是将线段首尾相接粘到一起。
example
考虑一个圆环 (1-sphere) 集合:
在其上装备继承于 的标准拓扑。在该圆环上的开集就是一些开圆弧;在其上的单独的点显然不是开集,因为无法在 上找到一个开集使其与该圆环只交于该点;但这样的单点是闭集,因为其补集是开圆弧,是开集。
针对上面这个圆环集合,还可以换一个角度考虑。考虑 上的等价关系 :
那么这个圆环可以看成集合 装备上其对应的 quotient topology
^example-quotient-2
problem
#todo 如果我们定义原集合M上的等价关系不是那么简单,参考^example-quotient-2中的集合和等价关系,按照定义,其quotient topology似乎是chaotic topology?
Product Topology
考虑 是 2 个拓扑空间,那么考虑 A 和 B 的笛卡尔积构成的新集合,给此新集合构造拓扑:
具体解释参考:

remark
这一product topology 很容易拓展到n-fold 的cartestian product 上,而这一结果的直接体现就是:
收敛性
为了定义收敛性,我们首先定义所谓的序列:
假定 M 是一个集合,M 中的一个序列 (sequence of points) 是一个映射
据此我们给出收敛的定义:
Convergence
假定 是一个拓扑空间,称 M 中的一个序列 q 是收敛到一个极限点 a:
^def-convergency
note
本身这一定义就很想大一的极限定义:对极限点的任意开邻域,存在足够大的N,使得对序列的N之后的点其落在这个开邻域中
现在我们将初步解答 chaotic topology 为什么这么“弱”, discrete topology 为什么这么”强“:
example
考虑给 M 装备 chaotic topology ,那么 M 中的任何序列收敛到 M 中的任何点,因为这个 chaotic topology 只有 1 个非空元素就是其本身
反过来,考虑装备 discrete topology,那么 只有基本上是常值的序列可以收敛,因为可以考虑极限点 a 的一个开邻域 (这确实是开邻域,既是开的,又包含 a),这意味着在足够大的 N 之后吗,序列就是 a
example
考虑一个集合 ,在其上考虑一个序列 ,那么 q 不是基本常值,因此在 其不是收敛的,但是在 上其是收敛的
连续性
continuity
是 2 个拓扑空间,且 是一个映射。那么我们说 是 连续的(针对其对应的拓扑),当且仅当:
其中 是 S 在映射 下的原相
总结来说,我们说映射是连续的,当且仅当开集的原相也是开集
^def-continuity
我的理解
#todo 或许反过来说上面的定义可能就不对了(约束太强)。比如考虑 , ,两者装备标准拓扑。映射 在这个3维空间中是一根直线,那么根据连续性定义,其不是连续的?因为对N中的一个开集,其原相对应的是一个开线段,在 的标准拓扑中似乎不是开的?
更进一步,考虑 ,映射 是一个直线,比如y轴,那么类似的理由,逆映射是一个点,也不是开的。
这两点共同在于似乎降维了,不知道对不对。和我们一般的理解连续可能不太一样
注意上面的映射并不是在M上所有元素有定义,是不是不符合我们定义?因为一般我们会有这暗示我们映射是在M上所有元素有定义的
example
我们考虑 M 装备 discrete topology 或者 N 装备 chaotic topology,那么任意映射 都是连续的。

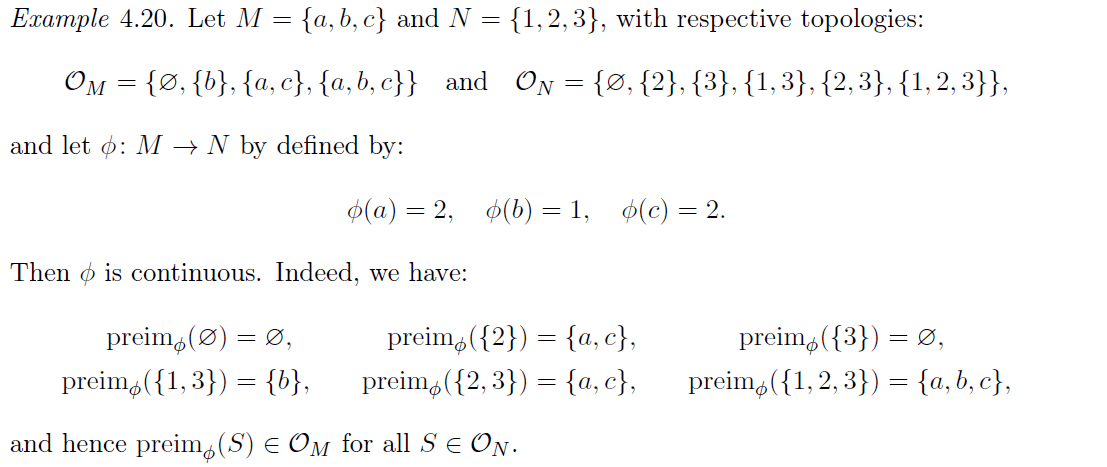
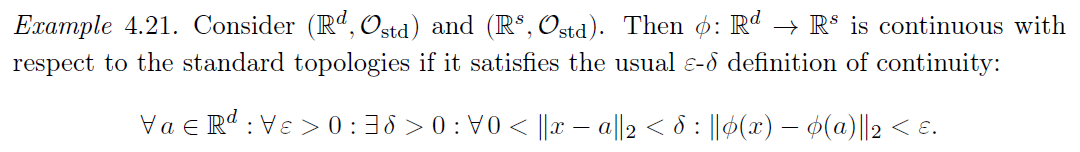
同胚
homeomorphism
我们考虑 是 2 个拓扑空间,有一个双射 是一个 同胚(homeomorphism),如果: 和 是连续的
^def-homeomorphism
同胚是在拓扑意义下保持 结构 的变换,类似于集合意义上的双射,不过保持了更多的结构信息。 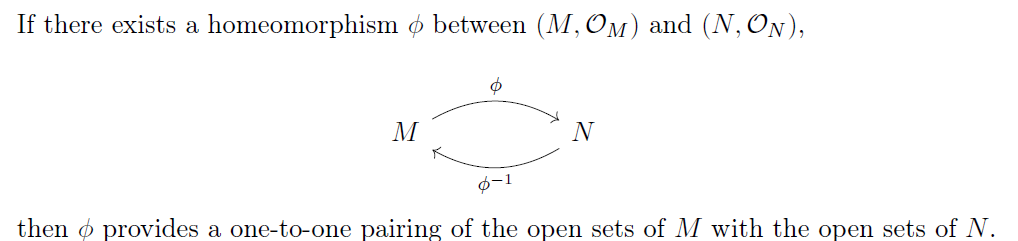
如果在 之间存在同胚,我们说这两个空间是同胚的 (homeomorphic) 或者说是拓扑同态的 (topologically isomorphic),记为
拓扑空间上的不变量
我们说不变量意思是说,两个 homeomorphic 的 space 共享这一个性质.
拓扑空间的分离性质
T1
我们称一个拓扑空间 是 T1 的,如果对任意两个 M 中的不同的点 :
这里的 代表一个包含 p 的开邻域。
^def-T1-topo
T2/hausdorff
我们称一个拓扑空间 是 T2 的 (Hausdorff),果如 M 中任意两个不同的点 :
^def-T2-topo
容易发现,标准 d 维空间 是 T2 的,因此是 T1 的;拓扑空间 不是 T1 也不是 T2 的。
remark
除了T1, T2之外,还有很多Tx,比如 和T2很想,只不过邻域是闭的
note
并不是说是T1的一定是T2,比如Zariski topology on an algebraic variety 是T1的而不是T2的
紧性和仿紧性
cover
对一个拓扑空间 ,称一个集合 是集合 M 的一个覆盖 (cover):
更进一步,如果 ,称 C 是一个开覆盖 (open cover)
^def-cover
subcover
针对 cover C,如果其中有一个子集 使得 也是一个覆盖,那么将 称为一个子覆盖 (subcover)。如果这个子集 是有限的 (作为集合 Axiom of Infinity),称是一个有限子覆盖
^def-subcover
在上面两个基础上,我们可以定义拓扑空间的 紧性:
compact
一个拓扑空间 是紧的 (compact),如果任何一个开覆盖存在有限子覆盖
^def-compact
根据 Induced Topology 的思想,我们自然会研究其上子集的紧性:
definition
如果拓扑空间 是拓扑空间, 被称为紧的,如果拓扑空间 是紧的
从紧性的定义来看,其涉及到一个存在性的证明,一般而言是不易证明的。但是,针对装备了标准拓扑的 而言,可以通过简单的判断方法决定其是否是紧的:
Heine-Borel
假定 装备了标准拓扑 ,那么 的一个子集是紧的,当且仅当其是闭的且有界的 (closed and bounded)
这里的有界指的是:
对上面的结论,也可以推广到任意的度量空间 (metric space)。
metric space
我们说一个度量空间是一个组 (pair):(M,d),其中 M 是一个集合, 是一个映射,对 有:
^def-metrix-space
example

注意例子5.7中的确实是一个单元素集合:,是R上标准拓扑的一个单元素子集,是开集,其势=1,因此是有限的
研究了子集的紧性后,还是按照延展拓扑性质的思想,考虑笛卡儿积的紧性:
theorem
假设 和 是 2 个紧的拓扑空间,那么装备了Product Topology的笛卡尔积空间是一个紧的拓扑空间
因为紧性是一个相当强的条件,很多时候我们没办法保证空间具有这个性质,因此退而求其次我们考虑一些更弱的性质。从而引出 refinemet 的定义:
refinement
假设 是一个拓扑空间,C 是一个覆盖。A refinement of C 是一个覆盖 R 使得:
直觉上来看,R 确实可以说的 C 的一个“精炼”,我们前面定义的子覆盖就是 refinement 的一个特例,但是反过来并不一定。
refinement 可以具有一些特性:
- 开的:如果 refinement R 满足
- locally finite:如果任意 存在一个开邻域 使得集合 是有限的
根据上面的性质,可以提出 paracompact 的定义:
paracompact
一个拓扑空间 是 paracompact 的,如果:任意开覆盖具有一个 open refinement 而且其是 locally finite 的
^def-paracompact
corollary
如果一个拓扑空间是紧的,那么他也是paracompact的
如果使用 paracompact 的定义,我们很难进行分析,因此给出下面一个简单的判断准则。
Stone
任何metrisable space 都是 paracompact的
其中 metrisable space 定义为:
一个拓扑空间 是 metrisable 的,如果存在一个度量 d 使得其导出的拓扑就是 ,也即
example
举例来说,我们知道 是 metrisable 的,因为其对应度量 ,从而其是 paracompact 的。
paracompactness 是一个非常普遍的性质,以至于找到的不具有这个性质的空间都是 " 人工雕琢 " 的,其中一个例子是 long line(Alexandroff line)。为了构造这一空间,我们首先注意到可以通过 来构造 ,而这个 long line L 就是被定义为:,其中 是一个不可数的无限集合。
现在我们有了 paracompact 和 compact,可以开始研究两者之间的关系了:
- 一个 paracompact 空间 和 compact 空间 ,考虑 装备上 product topology, 可以证明结果是 paracompact 的
- 这意味着,paracompact 是可传染的…
假设 是拓扑空间,定义 M 上的 partition of unity 是一个集合 F,其中包含的是从 M 到区间 的连续映射,且对 满足:
- 存在开邻域 使得集合 是有限的
如果 C 是一个开覆盖,称 是 subordinate to the cover C,如果:
关于这一点的讨论可以参考 [5]
remark


定义 partition of subordinate实际上是为了后面定义积分来做的,重点在于finite上来避免convergency的讨论
通过上面定义的 partition of unity 和 subordinate,我们可以更快的判断一些特殊空间是不是 paracompact 的:
theorem
假设 是一个 Hausdorff 拓扑空间,那么 是 paracompact 的当且仅当任何开覆盖 admits a partition of unity subordinate to that cover
example

note
感觉有种分段讨论的意思,可以将不同部分分开看?说不清楚...
Connectedness And Path-connectedness
从直觉上我们可以给出连通的定义:
connectedness
一个拓扑空间是连通的,除非存在 2 个非空、不相交的 开集A,B 使得:
^def-connect
note
注意既然是开集,那么连通与否自然和拓扑选取有关,比如我们选取chaotic topology, 那么所有的空间都是连通的
移动:我有话说
考虑 ,这个拓扑空间不是连通的,因为可以找到 2 个不相交的非空开集: 和 满足条件
根据定义,容易发现,一个拓扑空间 是连通的,当且仅当其既开又闭的子集仅为:
拓展定义,考虑定义:path-connectedness
path-connectedness
一个拓扑空间 被称为 path-connectedness, 如果任何一对点 ,存在一条连续的曲线 使得 ,。这里的连续性在 ^def-continuity 中定义
^def-path-connectedness
`::: note remark path-connectedness 是比 connectedness 更强的性质,连通的不一定可以找到这样的连续曲线,比如:
考虑 ,且装备了从 继承的拓扑,那么 是连通的,但不是 path-connectedness
::: functionplot
title: test xLabel: yLabel: bounds: [0,1,-1,1] disableZoom: false grid: true
f(x)=sin(1/x)
Homotopic Curves and the Fundamental Group
definition
考虑 中的 2 条曲线, 使得:
且存在一个连续映射 ,使得对所有的 :
称这两条曲线是 homotopic/同伦
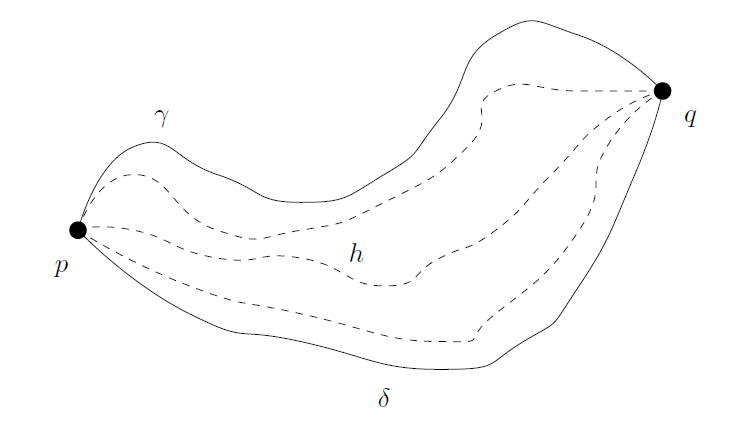
^def-homotopic
容易发现,同伦其实是一种 等价关系,那么我们可以在任意的拓扑空间上定义其对应的等价类,这就可以诱导出某种不变量。为此我们先定义 Space of loops
space of loops
考虑拓扑空间 , 对 M 中的所有点 定义 space of loops
^def-space-of-loop
在 space of loops 上,我们定义 concatenation 连接操作 (某种意义上的加法?):
从而我们可以导出一个等价类:
fundamental group
考虑 是拓扑空间,定义该空间的 p 点的 fundamental group 是集合:
这里的等价关系 指的是 homotopic(同伦)
在fundamental group上附带一个运算:
^def-fundamental-group
remark
注意,我们说一个群是一个集合附带一个 (双目) 运算构成的 pair:
此外,如果可交换 ,那么称这个群是阿贝尔群 (abelian/commutative)
类似集合的同构,可以定义群的 isomorphism:
在两个群 和 之间的 group isomorphism 是一个双射 使得:
如果 2 个群 和 之间存在 group isomorphism,我们称这两个群是 isomorphic(group),记为:
参考 Chap2 群
考虑一个 2-sphere(球面) 为:
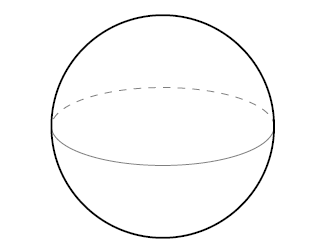
其上装备了从 上继承的拓扑。
该球面具有性质:任意一个点的任意 loop 都是 homotopic 的,从而我们知道在该球面上的 fundamental group(在任意点出) 是:
考虑一个无限长圆柱 ,装备了 Product Topology.
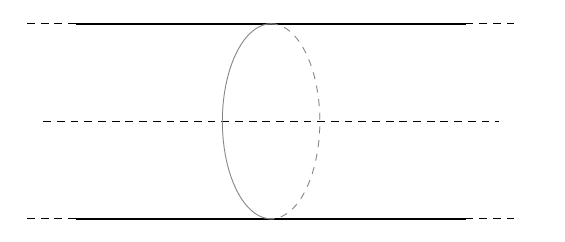
在 C 上的 loop 可以分为 2 种:绕着中心轴的,或者不绕中心轴的 (可以被连续地变形为一个点)。我们称绕着圆柱的次数为 winding number,具有不同 winding number 的 loop 是不同伦的
进一步,我们可以给出其 fundamental group 的结构:
考虑更复杂 的结构:2-torus:,其上装备了 product topology:
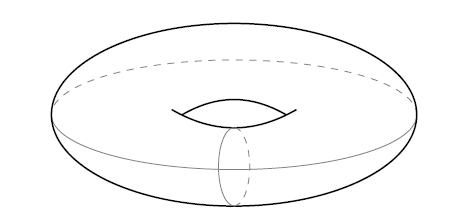
类似地可以发现,其 fundamental group 可以表示为:
其中 上的 + 是 pairwise addition.
