Chap2 群

Chap2 群

集合理论

一个群是一个集合，其元素可以被“乘”，而且乘法遵从一定的法则。一个有趣的例子是这类集合中的元素是函数的情形，更具体的，是一种在比较不同系统结构时浮现的函数 (同态)

从上面对群的定义，首先需要定义集合，并研究一些集合的特性

集合扩充

集合

一个集合X是一个元素的Collection，其中 $x\in X$ 意味着x属于X，即X中的元素列表中包含x

进一步容易定义集合是相等的，等价于两个集合有相同的元素

为了扩充集合的含义，引申出子集的定义：

子集

一个集合X的子集S等价于$\mathrm{if}s\in S\Rightarrow s\in X$

并不是所有集合都有元素，因此定义没有元素的集合为 $\varnothing$，代表没有元素的集合

集合运算

下面可以来定义集合上的运算了

• 交集

$$X\cap Y=\left\{z\in Z:z\in X\mathrm{and}z\in Y\right\}$$

• 并集

$$X\cup Y=\left\{z\in Z:z\in X\mathrm{or}z\in Y\right\}$$

• 差集

$$X-Y=\left\{x\in X:x\notin Y\right\}$$

函数

在定义了集合本身的特性后，下面可以来定义元素的操作了，即元素

我们最开始定义的函数是一种映射的思想，现在可以考虑换一个角度来考虑，将其写成一个“图形”的形式，即 (x,f(x))，下面给出这个想法的定义：

笛卡尔积(cartesian product)

如果X和Y是集合，我们定义其笛卡尔积(cartesian product) $X\times Y$ 是所有有序对(x,y)的集合，其中 $x\in X\mathrm{and}y\in Y$

• 更进一步，可以参考线性映射章节，可以发现 $\left|X\times Y\right|=\left|X\right|\left|Y\right|$

现在可以在笛卡尔积上定义 函数 了

函数

一个从X映射到Y的函数f，将其标识为 $f:X\to Y$，这个函数f是 $X\times Y$ 的一个子集，使得

$$\forall a\in X,\exists b=f\left(a\right)\in Y$$

对这样的 f，可以给出一些定义，对 $f:X\to Y$ 的形式，X 被称为 f 的 定义域 (domain)，Y 被称为 f 的 目标域 (target)，f 所有的元素构成的集合是 f 的 值域 (image)，其是 Y 的子集

给定了函数的定义后，类似集合的部分，可以定义函数上的运算了

函数的相等

一个函数 $f:X\to Y$ 和 $g:X^{\prime }\to Y^{\prime }$ 是相等的，等价于X=X’，Y=Y’而且子集 $f\subseteq X\times Y$ 和子集 $g\subseteq X^{\prime }\times Y^{\prime }$ 是相等的

从判定函数的相等的情况来看，一个函数有 3 个部分：

• domain X
• target Y
• 映射关系 我们称两个函数是相等的，等价于这三个子部分相等

由于函数 3 个部分都很重要，因此需要分析不同部分对函数本身的影响。对 domain 来说，可以定义下面的 函数限制：

限制函数

如果 $f:X\to Y$ 是一个函数，S是X的子集，那么定义f限制在S上构造了一个新函数：

$$f|S:S\to Y,\left(f|S\right)\left(s\right)=f\left(s\right)$$

对限制函数而言，可以自然地发现有这样的典范映射：

• S 是 X 的子集，则 包含关系 是一个典范映射：$i:S\to X,i\left(s\right)=s$

类似讨论线性映射的思路，我们可以定义单射和满射：

满射 (surjective)

一个函数 $f:X\to Y$ 是满射的，等价于：

$$\mathrm{range}f=Y$$

即任意y属于Y都有某个x属于X使得y=f(x)

单射 (injective)

一个函数 $f:X\to Y$ 是单射的，等价于：

$$\mathrm{null}f=\left\{0\right\}$$

即f(a)=f(b)等价于a=b

下面定义映射的复合

复合

如果 $f:X\to Y$ 而 $g:Y\to Z$，那么定义复合映射 $g\circ f$ 为：

$$g\circ f:x\to g\left(f\left(x\right)\right)$$

容易证明，复合运算是可结合的，即

$$\begin{array}{c}f:X\to Y,g:Y\to Z,h:Z\to W\\ h\circ \left(g\circ f\right)=\left(h\circ g\right)\circ f\end{array}$$

线性映射作为一个集合，还可以定义其逆映射，即：

$$\begin{array}{c}f:X\to Y,g:Y\to X\\ \mathrm{s}.\mathrm{t}.f\circ g=g\circ f=1\end{array}$$

这些都是在线性代数中厘清过的知识，这里不再多提

关系

关系

给定集合X和Y，X到Y的一个关系是指 $X\times Y$ 的一个子集R(根据前面对映射的定义这也就是一个映射)。如果X=Y，我们说R是X上的一个关系，通常写成 $XRY$

关系实际就是我们研究的线性映射，但我们这里主要关心关系的结构上的性质，而不关心其空间中的意义。因此这里将同构对应的 等价关系 定义为具有 3 条性质的关系

• 自反性：$x\equiv x\forall x\in X$
• 对称性：$x\equiv y\iff y\equiv x\forall x,y\in X$
• 传递性：$x\equiv y,y\equiv z\Rightarrow x\equiv z\forall x,y,z\in X$

有了等价关系，我们给定一个 $a\in X$，则可以得到 a 的等价类

等价类

$$\left[a\right]=\left\{x\in X:x\equiv a\right\}\subseteq X$$

等价类一个经典的例子就是整数域上的模运算生成的 mod n 等价类

我们可以把等价类看成一个元素的特征的描述，在这个特征意义下，这个等价类就可以代替元素本身，因此引发我们考虑下面的定理：

lemma

$$x\equiv y⟺\left[x\right]=\left[y\right]$$

使用等价关系的传递性和对称性容易证明上面结论

从集合论的角度来看，等价关系将一个集合划分成了很多块，这是一种 分割，我们可以说，等价关系和集合的分割是等价的

置换

置换和排列(permutation & arrangement)

• 一个集合X的置换 (permutation)是一个双射 $\alpha :X\to X$，其中X是一个长度为n的有限集合。
• 一个集合X的排列(arrangement)是一个列表 $x_1,x_2,\cdots ,x_n$ 且不含有X的重复元素

note

置换是一个映射，而排列是置换的值域上的元素

给定一个排列 $x_1,x_2,\cdots ,x_n$，定义函数 $f:\left\{1,2,\cdots ,n\right\}\to X,f\left(i\right)=x_i$，则上面排列是 f 的值域。由于排列上没有重复元素，表明 f 是单射；又因为每个 X 上的元素都出现在排列中，说明 f 是一个满射，从而表明，一个排列定义了一个双射 $f:\left\{1,2,\cdots ,n\right\}\to X,f\left(i\right)=x_i$

举例来说： ^eqn-two-row-notation-permutation

note

上面描述稍微有点不严谨，置换作用在X上而不是Rn上，不过是同构的，因此加一个复合就行

我们可以说，排列 (lists) 和置换 (双射) 是两个描述集合位置更改的方式，从置换角度看，双射作为映射的好处是可以和别的映射复合，在我们的运算上更加便利

definition

根据置换的定义，这是一个双射。将所有置换构成的集合记为 $X$，记为 $S_X$，被称为X上的对称群。

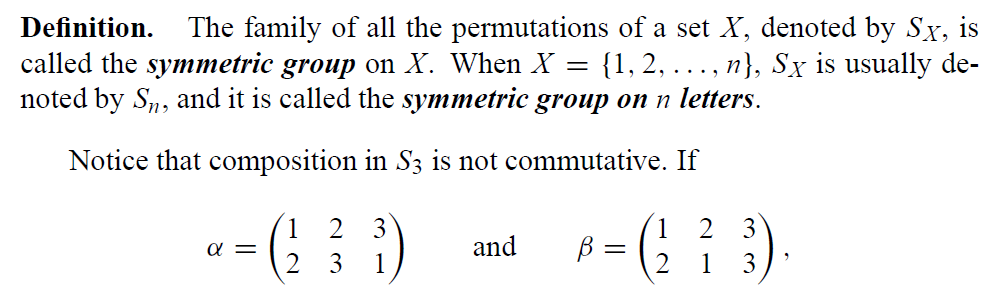
注意这个群上的复合运算是不可交换的（尽管有些可以交换来着）

但对定义的对称群，其满足特别的性质 消去律

$$\mathrm{if}\gamma \circ \alpha =\gamma \circ \beta ,\mathrm{then}\alpha =\beta$$

$$\begin{array}{rl}\alpha & =1_X\circ \alpha \\ & =\left({\gamma }^{-1}\circ \gamma \right)\circ \alpha \\ & ={\gamma }^{-1}\circ (\gamma \circ \alpha )\\ & ={\gamma }^{-1}\circ (\gamma \circ \beta )\\ & =\left({\gamma }^{-1}\circ \gamma \right)\circ \beta \\ & =1_X\circ \beta =\beta \end{array}$$

类似可以证明：

$$\mathrm{if}\alpha \circ \gamma =\beta \circ \gamma ,\mathrm{then}\alpha =\beta$$

使用前面定义的 二行记号，尽管可以直观的展示映射关系，但对我们理解映射性质带来了干扰：

• 一个置换的平方是什么样子？不能直接看出
• 可以经过多少次置换使得其变为恒等的？

下面针对上面提出的问题，给出一个特殊的置换定义来解决这些问题：

definition

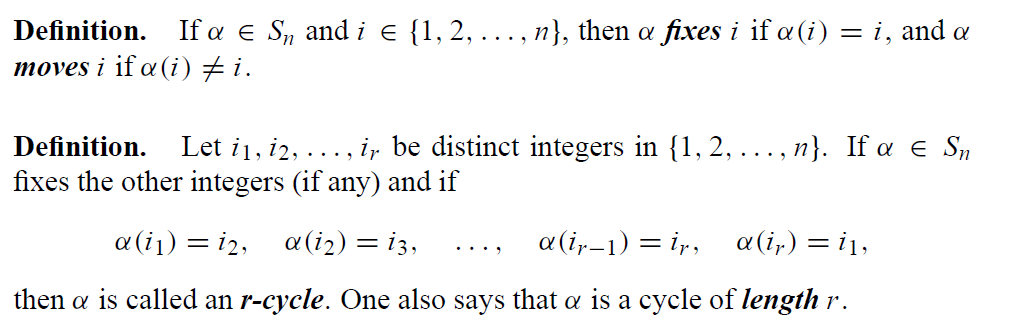循环置换

^eqn-cycle-permutation

comment

已经开始引入对称性了

对上面的定义，一个 2- 循环置换交换 2 个元素，并固定其余所有元素。1- 循环置换则是群上的单位元素。

对比 2 行记号形式，其不能帮我们认识到下面的情形：

现在，为了更形式化的表述 r- 循环置换，引入新记号：

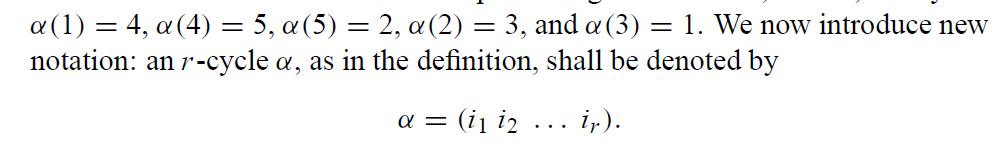
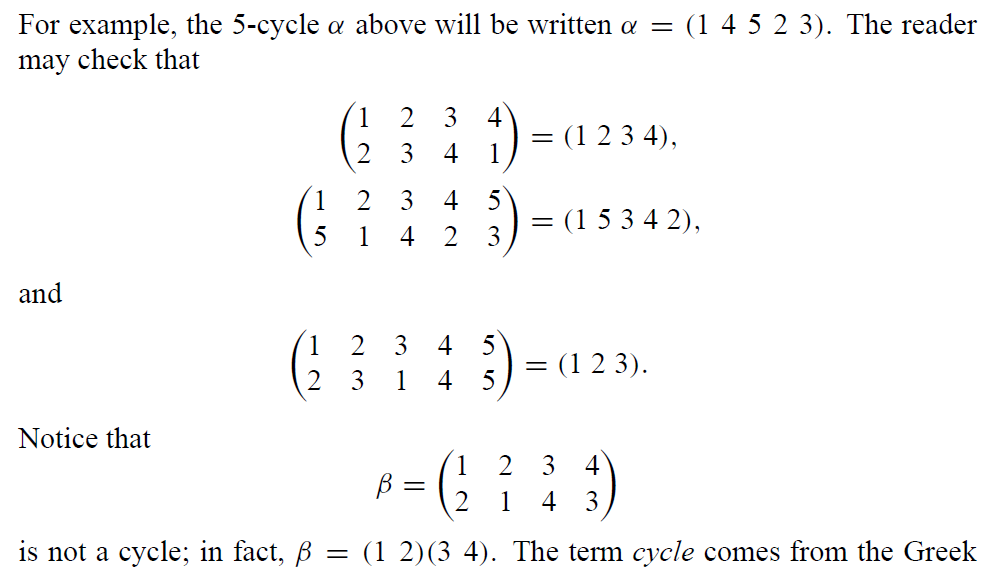
note

可以注意到，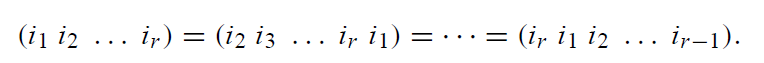

因此一个r-置换有r个不同的记法

置换的应用

我们给出一个算法，可将 置换分解为循环置换的乘积

根据上面的复合法则，可以方便的得到置换的表示

但可以注意到，这样的表示方法可能并不是最简单的！比如下面的例子：

对 $\sigma$ 而言，根据我们的运算规则，实际上可以被化简为

$$\sigma =\left(14\right)\left(2\right)\left(35\right)$$

不相交置换

definition