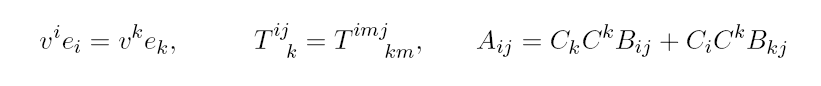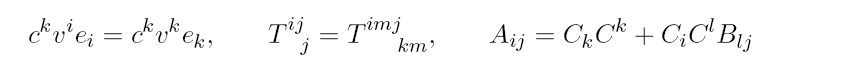Chap5 张量空间

什么事张量

向量空间和其对偶

详细的关于向量空间的介绍可以参考 从线性映射理解线性代数 和 抽象代数基础教程抽象代数基础教程，这里给出一些简单的介绍

域

field/域

一个 (algebraic) field 事一个三元组 $(K,+,\cdot )$，其中 K 是一个集合，$+,\cdot$ 是双目运算：$K\times K\to K$ 且满足下面性质：

1. $(K,+)$ 是一个阿贝尔群，即：
   1. $\forall a,b,c\in K:(a+b)+c=a+(b+c)$
   2. $\exists 0\in K:\forall a\in K:a+0=0+a=a$
   3. $\forall a\in K:\exists -a\in K:a+(-a)=(-a)+a=0$
   4. $\forall a,b\in K:a+b=b+a$
2. $(K^{\ast },\cdot )$，其中 $K^{\ast }:=K\backslash \left\{0\right\}$，是一个阿贝尔群，即：
   1. $\forall a,b,c\in K^{\ast }:\left(a\cdot b\right)\cdot c=a\cdot (b\cdot c)$
   2. $\exists 1\in K^{\ast }:\exists a\in K^{\ast }:a\cdot 1=1\cdot a=a$
   3. $\forall a\in K^{\ast }:\exists a^{-1}\in K^{\ast }：a\cdot a^{-1}=a^{-1}\cdot a=1$
   4. $\forall a,b\in K^{\ast }:a\cdot b=b\cdot a$
3. 映射 $+$ 和 $\cdot$ 满足分配律: 9. $\forall a,b,c\in K:(a+b)\cdot c=a\cdot c+b\cdot c$

^def-group-field

remark

一个阿贝尔群是一个比较好的数学结构，与之相似的但是更弱的是环 (ring)，其虽然也是一个三元组，不需要性质 2.2,2.3,2.4。如果一个环满足性质 2.2，那么称其为 unital ring(单位环)，如果其满足性质 2.4，那么称其为 commutative ring(交换环)，我们一般考虑的是 unital ring，而且一般就称为 ring

• 一个三元组 $(\mathbb{Z},+,\cdot )$ 是一个交换的单位环，然而其不是一个域 (field)，因为其中仅有 $1,-1$ 可以做逆运算 (性质 2.3)
• 集合 $\mathbb{Q},\mathbb{R},\mathbb{C}$ 装备常规的 $+,\cdot$ 就是一个域
• 实 $m\times n$ 矩阵 $M_{m\times n}(\mathbb{R})$ 是一个非交换的环

向量空间

K-vector space

假定 $(K,+,\cdot )$ 是一个域，在 K 上的一个 K-vector space 被定义为一个三元组：$\left(V,\oplus ,\odot \right)$，其中 V 是一个集合，且：

$$\begin{array}{r}\oplus :V\times V\to V\\ \odot :K\times V\to V\end{array}$$

满足：

• $(V,\oplus )$ 是一个阿贝尔群
• 映射 $\odot$ 是一个在 $(V,\odot )$ 上的对 K 的 action：
  • $\forall \lambda \in K:\forall v,w\in V:\lambda \odot (v\oplus w)=(\lambda \odot v)\oplus (\lambda \odot w)$
  • $\forall \lambda ,\mu \in K:\forall v\in V:\left(\lambda +\mu \right)\odot v=\left(\lambda \odot v\right)\oplus \left(\mu \odot v\right)$
  • $\forall \lambda ,\mu \in K:\forall v\in V:\left(\lambda \cdot \mu \right)\odot v=\lambda \odot \left(\mu \odot v\right)$
  • $\forall v\in V:1\odot v=v$

^def-k-vector-space

vector space 也被称为 linear space，其中的元素被称为向量，域 K 中的元素被称为标量，映射 $\odot$ 被称为标量乘法 (scalar multiplication)

上面的定义和我们之前对线性代数的操作是兼容的，因此可以预见到一些剩余的定义：

线性子空间

假定 $(V,\oplus ,\odot )$ 是一个 K 上的线性空间，集合 $U\subseteq V$ 是非空的，那么我们可以构造线性子空间 $(U,\oplus {|}_{U\times U},\odot {|}_{K\times U})$ ：

• $\forall u_1,u_2\in U:u_1\oplus u_2\in U$
• $\forall u\in U:\forall \lambda \in K:\lambda \odot u\in U$

也可以写为：$\text{if}\forall u_1,u_2\in U:\forall \lambda \in K:(\lambda \odot u_1)\oplus u_2\in U$

^def-vector-subspace

和研究拓扑空间的思路一样，除了向内探求，扩充子空间的方式来增加空间种类，还可以向外探求，通过笛卡尔积来 product 空间

在基本的空间构造完了后，现在来研究映射保证空间上结构不变

线性映射

线性映射

如果 $(V,\oplus ,\odot ),(W,⊞,⊡)$ 是在域 K 上的向量空间，映射 $f:V\to W$，我们说 f 是一个线性映射，如果 $\forall v_1,v_2\in V,\forall \lambda \in K$ :

$$f((\lambda \odot v_1)\oplus v_2)=(\lambda ⊡f(v_1))⊞f(v_2)$$

^def-linear-map

为了方便，我们将不再使用类似 $\odot ,⊞$ 之类的特殊符号，直接使用 $\cdot ,+$ 来表示标量乘法和向量加法，其作用域隐含在 context 中

线性同构

我们称一个线性双射是一个线性空间上的线性同构 (linear isomorphism)，2 个线性空间被称为isomorphic，记为$V{\cong }_{\text{vec}}W$

^def-linear-isomorphic

note

可以直接证明，一个线性映射 $\varphi$，如果是双射，那么其逆映射 ${\varphi }^{-1}$ 也是线性的

根据我们之前学习线性代数的思路，在完善了线性映射的定义后，下面可以来研究线性映射构成的新空间，之前的结论告诉我们，这也是一个线性空间

对偶空间

线性映射的空间

$V,W$ 是 K 上的线性空间，集合：

$$\text{Hom}(V,W):=f|f:V\stackrel{\sim }{\to }W$$

其中记号 $f:V\stackrel{\sim }{\to }W$ 代表 f 是 V 到 W 的线性映射

^def-linear-map-space

容易构造出一个新的线性空间，其上的 $+,\cdot$ 分别定义为：

$$\begin{array}{rl}\oplus :\text{Hom}(V,W)\times \text{Hom}(V,W)& \to \text{Hom}(V,W)\\ (f,g)& \mapsto f\oplus g\end{array}$$

其中：

$$\begin{array}{rl}f\oplus g:V& \stackrel{\sim }{\to }W\\ v& \mapsto (f\oplus g)(v):=f(v)+g(v)\end{array}$$

$$\begin{array}{rl}\odot :K\times \text{Hom}(V,W)& \to \text{Hom}(V,W)\\ (\lambda ,f)& \mapsto \lambda \odot f\end{array}$$

其中：

$$\begin{array}{rl}\lambda \odot f:V& \stackrel{\sim }{\to }W\\ v& \mapsto (\lambda \odot f)(v):=\lambda f(v)\end{array}$$

remark

注意到，在我们证明向量空间的性质时，实际上并没有使用到全部的域的性质，事实上只需要K是一个(unital) ring 就足够了。在ring上的向量空间被称为 modules (模)

尽管在域上，Hom(V,W) 可以被很好的构造出来，但是如果是在环上定义的模，Hom 就不一定是向量空间了，因为证明其为向量空间利用到了乘法的交换性，但在环上不一定成立

介绍了 Hom 的构造，熟悉线性代数思路的 boy 应该会想到将其“特殊化”，考虑特殊的线性映射，这会诱导我们构造出所谓的对偶空间！

endomorphism

V 是一个线性空间，称 V 上的一个 endomorphism 是一个线性映射集合 $V\to V$，记为：$\text{End}(V):=\text{Hom}(V,V)$

^def-endomorphism

automorphism

如果 V 是一个线性空间，称 V 上的一个 automorphism 是一个线性同构集合$V\to V$，记为： $\text{Aut}(V):=\left\{f\in \text{End}(V)|f\text{ is an isomorphism}\right\}$

^def-automorphism

remark

$\text{Aut}(V)$并不是一个线性空间，而$\text{End}(V)$是一个线性空间；但是$\text{Aut}(V)$是一个group，在线性映射复合的运算下

终于我们可以给出对偶空间的定义：

对偶空间

V 是 K 上的一个线性空间，称其对偶空间 $V^{\ast }$ 为：

$$V^{\ast }:=\text{Hom}(V,K)$$

此时 K 作为一个线性空间来考虑，可以证明域 K 就是一个线性空间

^def-dual-space

对偶空间中的元素是那些将 V 映射到 K 上的线性映射，一般也可以被称为线性算子 (linear functionals, covectors, or one-forms on V)

我们在线性空间的基础上导出了其对偶空间，接下来将介绍，通过研究向量空间和其对偶空间，我们可以构造出更抽象的张量空间和张量积

张量和张量空间

为了研究张量，我们首先给出所谓的 双线性 的定义，可以参考 ^[1]

双线性

假定 $V,W,Z$ 是在 K 上的向量空间，映射 $f:V\times W\to Z$ 被称为双线性的 (bilinear)，如果：

• $\forall w\in W:\forall v_1,v_2\in V:\forall \lambda \in K:f(\lambda v_1+v_2,w)=\lambda f(v_1,w)+f(v_2,w)$
• $\forall v\in V:\forall w_1,w_2\in W:\forall \lambda \in K:f(v,\lambda w_1+w_2)=\lambda f(v,w_1)+f(v,w_2)$

即对映射 $v\mapsto f(v,w)$ 和 $w\mapsto f(v,w)$ 对任意固定的 w 和 v 都是线性的

remark

如果将 $V\times W$ 看成一个整体，考虑线性映射 $f:V\times W\stackrel{\sim }{\to }Z$ ：

$$\forall x,y\in V\times W:\forall \lambda \in K:f(\lambda x+y)=\lambda f(x)+f(y)$$

如果展开来看，$x=(v_1,w_1),y=(v_2,w_2)$，有：

$$f(\lambda (v_1,w_1)+(v_2,w_2))=\lambda f((v_1,w_1))+f((v_2,w_2))$$

对比我们定义的双线性：

$$\begin{array}{rl}f(\lambda v_1+v_2,\mu w_1+w_2)& =\lambda f(v_1,\mu w_1+w_2)+f(v_2,\mu w_1+w_2)\\ & =\lambda (\mu f(v_1,w_1)+f(v_1,w_2))+(\mu f(v_2,w_1)+f(v_2,w_2)\end{array}$$

显然和线性映射不同，这意味着双线性其实是一种特殊的非线性

example

映射 $f:{\mathbb{R}}^2\to \mathbb{R}$ ，定义为 $(x,y)\mapsto x+y$，可以验证这是一个线性映射：

$$f(\lambda (x_1,y_1)+(x_2,y_2))=(\lambda x_1+x_2)+(\lambda y_1+y_2)=\lambda f(x_1,y_1)+f(x_2,y_2)$$

而对定义为 $(x,y)\mapsto xy$，其不是一个线性映射，但是是一个双线性映射：

$$\begin{array}{rl}f(\lambda x_1+x_2,y)=(\lambda x_1+x_2)y& =\lambda f(x_1,y)+f(x_2,y)\\ f(x,\lambda y_1+y_2)=x(\lambda y_1+y_2)& =\lambda f(x,y_1)+f(x,y_2)\end{array}$$

根据双线性的思想 (对单个 index 线性)，我们可以拓展到多重线性映射 (通过笛卡尔积)，从而可以给出张量的定义了：

多重线性映射/张量

V 是一个 K 上的向量空间，一个 $(p,q)$-tensor T 在 V 上是一个多重线性映射：

$$T:\underset{p\text{ copies}}{\underbrace{V^{\ast }\times \cdots V^{\ast }}}\times \underset{q\text{ copies}}{\underbrace{V\times \cdots \times V}}\to K$$

我们可以记为：

$$T_q^{p}V:=\underset{\text{just a notation now}}{\underbrace{\underset{p\text{ copies}}{\underbrace{V\otimes \cdots \otimes V}}\otimes \underset{q\text{ copies}}{\underbrace{V^{\ast }\otimes \cdots \otimes V^{\ast }}}}}:=\left\{T|T\text{ is a }(p,q)\text{-tensor on }V\right\}$$

^def-tensor

我们称 $(p,0)$ 张量是协变张量 (covariant p-tensor)，$(0,q)$ 是逆变张量 (contravariant q-tensor)

remark

传统上来说，$(0,0)$ 张量就是 K 上的一个元素，因此记为$T_0^0=K$

remark

注意，为了定义 $T_q^{p}V$ 是一个集合，回顾我们集合的定义，我们需要写出一个形式化的，反映集合元素特征的定义。注意到，我们目前讲的映射实际上是一个 relation，即：$f:A\to B$ 是一个 relation $A\times B$ 的子集，因此满足某个特征 $p$ 的映射 $f$ 可以表示为：

$$\left\{f\in \mathcal{P}(A\times B)|(f:A\to B)\wedge p(f)\right\}$$

因此，对 $T_q^p$ 的集合表示，实际上指的是：

$$T_q^{p}V:=\left\{T\in \mathcal{P}(\underset{p\text{ copies}}{\underbrace{V^{\ast }\times \cdots V^{\ast }}}\times \underset{q\text{ copies}}{\underbrace{V\times \cdots \times V}}\times K)|T\text{ is a }(p,q)\text{-tensor on }V\right\}$$

remark

对集合 $T_q^{p}V$ 上可以装备一个 K-vector space，定义 $\oplus ,\odot$ 如下：

$$\begin{array}{rl}\oplus :T_q^{p}V\times T_q^{p}V\to & T_q^{p}V\\ (T,S)\to & T\oplus S\end{array}$$

$$\begin{array}{rl}\odot :K\times T_q^{p}V\to & T_q^{p}V\\ (\lambda ,T)\to & \lambda \odot T\end{array}$$

其中 $T\oplus S,\lambda \odot T$ 是逐元素定义的，可以参考 Hom(V,W) 的定义，完全一样的思路

^remark-tensor-linear-space

为了从现有的线性空间 tensor space 中构造新的 tensor，正如我们一贯的思路：

• 向内找子空间
• 向外找 product

这次向内似乎不好找，或者说目前看来意义不大 (张量空间上目前也没有什么结构可以继承到子空间上？)，我们向外探索 product，因此：张量积，堂堂登场！

张量积

取张量 $T\in T_q^{p}V,S\in T_s^{r}V$，定义 T 和 S 的张量积 $T\otimes S\in T_{q+s}^{p+r}V$：

$$\begin{array}{rl}(T\otimes S)(w_1,\cdots ,w_p,& w_{p+1},\cdots ,w_{p+r},v_1,\cdots ,v_q,v_{q+1},\cdots ,v_{q+s}):=\\ & T(w_1,\cdots ,w_p,v_1,\cdots ,v_q)S(w_{p+1},\cdots ,w_{p+r},v_{q+1},\cdots ,v_{q+s})\end{array}$$

其中 $w_i\in V^{\ast },v_i\in V$

^def-tensor-product

note

#todo 这里的张量积和前面的符号 $\otimes$ 是混用的？？？^def-tensor

关于张量积的引入，可以参考：

• 为什么要定义张量积? - 知乎

example

• $T_1^{0}V:=\left\{T|T:V\stackrel{\sim }{\to }K\right\}=\text{Hom}(V,K)=V^{\ast }$
• $T_1^{1}V:=V\otimes V^{\ast }:=\left\{T|T\text{ is a bilinear map}{V}^{\ast }\times V\to K\right\}$，我们可以证明其和 $\text{End}(V^{\ast })$ 是一样的。具体来说，取 $T\in V\otimes V^{\ast }$，我们可以构造一个 $\hat{T}\in \text{End}(V\ast )$：

$$\begin{array}{rl}\hat{T}:V^{\ast }\stackrel{\sim }{\to }& V^{\ast }\\ w\mapsto & T(w,-)\end{array}$$

其中 $T(w,-):V\to K\in V^{\ast }$，这表明构造成立；反过来也是类似的构造，且构造的映射的线性可以直接从双线性性得到。从而我们构造了一个双射，从而有 $T_1^{1}V{\cong }_{\text{vec}}\text{End}(V^{\ast })$

• $T_0^{1}V{≆}_{\text{vec}}V$，一般来说这是不成立的，有限维的时候成立
• $T_1^{1}V{≆}_{\text{vec}}\text{End}(V)$
• $(V^{\ast }{)}^{\ast }{\cong }_{\text{vec}}V$，当 V 有限维时成立，所谓的自然同构

在线性空间中，为了确定坐标，我们需要给出一组基底，而唯一的不依赖任何额外的结构的基底是 Hamel basis

Hamel basis

如果 $(V,+,\cdot )$ 是在 K 上的线性空间，子集 $\mathcal{B}\subseteq V$ 被称为 V 的 Hamel basis，如果：

• $\mathcal{B}$ 的每个有限子集 $\left\{b_1,\cdots ,b_N\right\}$ 都是线性不相关的，即 ${\sum }_{i=1}^N{\lambda }^i{b}_i=0\Rightarrow {\lambda }^i=0$
• $\mathcal{B}$ 是 V 的一个 generating/spanning set，即：$\forall v\in V:\exists v^1,\cdots ,v^M\in K,\exists b_1,\cdots ,b_M\in \mathcal{B}:v={\sum }_{i=1}^M{v}^i{b}_i$
  • 上面定义也可以转换为如下表示：

$${\text{span}}_K(\mathcal{B}):=\left\{\sum _{i=1}^n{\lambda }^i{b}_i|{\lambda }^i\in K\wedge b_i\in \mathcal{B}\wedge n\ge 1\right\}$$

从而有 $V={\text{span}}_K(\mathcal{B})$

^def-hamel-basis

Hamel Basis 有一些有用的性质：

• V 是一个向量空间，$\mathcal{B}$ 是 V 的一组 hamel basis，那么 $\mathcal{B}$ 是一个 minimal spanning and maximal independent subset of V，即，如果 $S\subseteq V$，有
  • $\text{span}(S)=V\Rightarrow \left|S\right|\ge \left|\mathcal{B}\right|$
  • S 是线性独立的 $\Rightarrow \left|S\right|\le \left|\mathcal{B}\right|$

我们定义线性空间的维数为：$\left|V\right|:=\left|\mathcal{B}\right|$，其中 $\mathcal{B}$ 是线性空间 V 的 Hamel basis，我们可以证明，对一个给定的线性空间，其不同的 hamel basis 具有相同的势，那么表明我们的定义是 well-defined

如果我们对有限维线性空间 V 选取了 hamel basis 有：$\mathcal{B}=\left\{e_1,\cdots ,e_{dimV}\right\}$，那么可以构造 $v^{\ast }$ 上的对偶基: ${\mathcal{B}}^{\prime }=\left\{f^1,\cdots ,f^{dimV}\right\}$ ：

$$\forall 1\le i,j\le dimV:f^i(e_j)={\delta }_j^i:=\{\begin{array}{ll}1& \text{if }i=j\\ 0& \text{if }i\ne j\end{array}$$

^eqn-induced-dual-basis

可以证明，这是满足定义的对偶基，这也给我们信息：在有限维的情形，V 和 V* 和 (V*)* 都是同构的，且保持了线性性

一旦我们有了空间中的基底，我们就可以将空间中的元素在基底下进行表示，从而将坐标对这种东西扩展到张量上：

tensor components

V 是一个 K 上的有限维线性空间，有基底 $\mathcal{B}=\left\{e_1,\cdots ,e_{dimV}\right\}$，取张量 $T\in T_q^{p}V$，我们定义 T 在基底 B 下的 components 为：

$$T_{b_1\cdots b_q}^{a_1\cdots a_p}:=T(f^{a_1},\cdots ,f^{a_p},e_{b_1},\cdots ,e_{b_q})\in K$$

其中 $1\le a_i,b_j\le dimV$是数，$\left\{f^1,\cdots ,f^{dimV}\right\}$ 是 B 的对偶基

^def-tensor-componenets

remark

一般来说，我们取 B 对偶基是从 B 的基里面诱导出的 (虽然你可以取不一样的)，即：

^eqn-induced-dual-basis

如果我们将一个 tensor T 表示成了一堆数字 $(a_1,\cdots ,a_p|b_1,\cdots ,b_q):=T_{b_1,\cdots ,b_q}^{a_1,\cdots ,a_p}$，那么应该如何将其重构回一个抽象的多重线性映射呢？

根据张量的 components，我们可以重构张量：

$$T=\underset{p+q\text{times}}{\underbrace{\sum _{a_1=1}^d\cdots \sum _{b_q=1}^d}}{T}_{b_1\cdots b_q}^{a_1\cdots a_p}\odot e_{a_1}\otimes \cdots \otimes e_{a_p}\otimes f^{b_1}\otimes \cdots \otimes f^{b_q}$$

^eqn-reconstruct-tensor

其中 $e_{a_i}$ 代表 $T_0^1{\cong }_{\text{vec}}V$ 的元素，$f^{b_i}$ 代表 $T^{0}1V{\cong }_{\text{vec}}{V}^{\ast }$ 的元素。根据我们定义的张量积计算方法，^def-tensor-product，$e_{a_1}\otimes \cdots \otimes e_{a_p}\otimes f^{b_1}\otimes \cdots f^{b_q}$ 是 p 个 $T_0^1$ 张量和 q 个 $T_1^0$ 之张量积，因此结果为一个 $T_q^p$ 张量。我们在前面已经给出了 tensor space 作为 线性空间的结构，其中给出了其上的 scalar 运算符号 $\odot$。根据我们张量积的定义，将还原后的结果丢进去算，可以发现结果正确，这表明我们的还原映射操作大成功！

note

在表示^eqn-reconstruct-tensor时，其中的求和符号我们一般省略掉，根据后面的求和指标约定。

简单来说，V的基底放在下方，$V^{\ast }$的基底放在上方，一旦出现上方下方一样指标，就直接求和。

具体可以参考后面部分Einstein Summation Convention

我们完成了在给定基底下张量的分量表示，并对分量表示进行了还原。下面我们可以考虑，如果有 2 个不同的基底，那么基底之间的转换应该如何表示？

考虑一个有限维向量空间，$dimV=d$，有基底：$e_1,\cdots ,e_d$，新基底为：

$${\overline{e}}_a=\sum _{b=1}^d{A}_a^b\cdot e_b,a=1,\cdots ,d$$

，其中 $A_a^b\in K$(输入 2 个变量，输出一个 scalar)，而其对应的运算 $\cdot =\odot$，即在线性空间 V 上定义的 scalar product。为了保证新基底确实是一个基底，应该还可以转换回去，即：

$$e_a=\sum _{b=1}^d{B}_a^b\cdot {\overline{e}}_b,a=1,\cdots ,d$$

如果采用矩阵记号，我们有 $A^{-1}=B$

Einstein Summation Convention

首先展示基本例子：

我们写出：

$$v=v^i{e}_{i}T=T_k^{ij}{e}_i\otimes e_j\otimes f^k$$

而不是：

$$v=\sum _{i=1}^d{v}^i{e}_{i}T=\sum _{i=1}^d\sum _{j=1}^d\sum _{k=1}^d{T}_k^{ij}{e}_i\otimes e_j\otimes f^k$$

我们将上下重复的指标称为哑指标 (dummy indices)，他们总是成对出现在上下部分，我们将其加起来；不是哑指标的 indices 我们称为自由指标 (free indices)；包含自由指标的式子代表多个表达式，每一个自由指标代表一个 slot 的位置 (对应该 slot 上多个值对应的表达式)，且自由指标必须在等式两边匹配：

• 正确式子：
  • 
• 不正确式子：
  • 

一般来说：

• V 的基底写在下方
• V 对偶基底写在上方

举例来说：

• $f^a(v)=f^a(v^b{e}_b)=v^b{f}^a(e_b)=v^b{\delta }_b^a=v^a$
• $w(e_b)=(w_a{f}^a)e_b=w_a{f}^a(e_b)=w_b$
• $w(v)=(w_a{f}^a)(v^b{e}_b)=w_a{v}^a$

其中 $v\in V,w\in V^{\ast }$, $\left\{e_i\right\}$ 是 V 的基，$\left\{f^j\right\}$ 是 V 的对偶基

remark

注意，Einstein 的求和规则只适用于线性空间和多重线性映射，否则看下面这个情况：

考虑一个映射 $\varphi :V\times W\to Z$，取 $v=v^i{e}_i\in V$，$w=w^i{\overline{e}}_i\in W$，从而有：

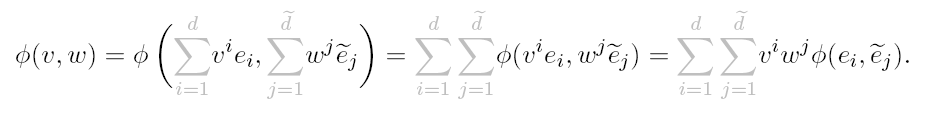
注意上面式子推出最后一步依赖于 $\varphi$ 是双线性的 (从而针对每个 slot 都是线性的，才能提出 $v^i,w^j$)

线性代数里面我们给出了行向量和列向量。我们在了解了指标过后很容易想到这样的理解：

考虑 $v=v^i{e}_i\in V$，$w=w_i{f}^i\in V^{\ast }$，将其看成下面的情况：

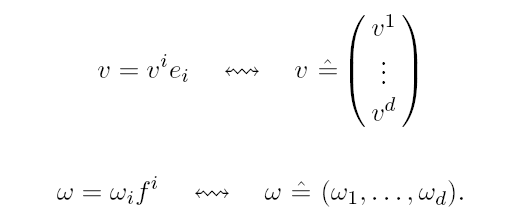
注意到 $T_1^{1}V{\cong }_{vec}End(V)$，因此取 $\varphi \in End(V)$，利用张量的分解我们有：$\varphi ={\varphi }_j^i{e}_i\otimes f^j$，其中 ${\varphi }_j^i:=\varphi (f^i,e_j)$ 是映射 $\varphi$ 在给定基地下的分量。回忆矩阵的想法，我们或许会写成：

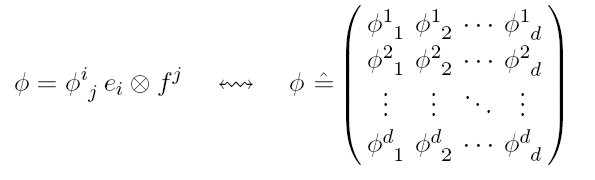
表示成这样带来了结构上的复杂性，但是也有一定的好处

考虑有限维线性空间 V，我们有：$\varphi \in T_1^1(V){\cong }_{\text{vec}}End(V)$，那么有：

$$\varphi (w,v):=w(\varphi (v))$$

因此对 $\varphi \in End(V)$ 的分量，我们可以写为：${\varphi }_b^a:=f^a(\varphi (e_b))$

注意到如果 $\varphi ,\psi \in End(V)$，那么考虑复合 $\varphi \circ \psi$：

$$\begin{array}{rl}(\varphi \circ \psi {)}_b^a& :=(\varphi \circ \psi )(f^a,e_b)\\ & :=f^a((\varphi \circ \psi )(e_b))\\ & =f^a(\varphi (\psi (e_b)))\\ & =f^a(\varphi ({\psi }_b^m{e}_m))\\ & ={\psi }_b^m{f}^a(\varphi (e_m))\\ & ={\psi }_b^m{\varphi }_m^a\end{array}$$

最后一行就是在域 K 上进行的乘法，域 K 上乘法是可交换的，因此 ${\psi }_b^m{\varphi }_m^a={\varphi }_m^a{\psi }_b^m$。如果使用我们前面给出的矩阵记号，后面一个就是矩阵乘法

类似的，考虑：

$$\begin{array}{rl}w(v)=w_m{v}^m& \iff w^{T}v\\ \varphi (w,v)=w_a{\varphi }_b^a{v}_b& \iff w^T\varphi v\end{array}$$

不幸的是，transpose 是很容易造成误解的，是一个很坏的 notation…比如参考 ^example-matrix-flaw 是其中一个问题 #todo

这个故事的寓意是,你应该尽力不要把向量、向量和张量看作数字数组。相反,总是试着从抽象的、内在的、没有组件的角度来理解它们。

前面介绍了换基的部分操作，即：

有 V 的 2 组基 $\left\{e_a\right\}$ 和 $\left\{{\overline{e}}_a\right\}$，不同基底下应该有：${\overline{e}}_a=A_a^b{e}_b$，$e_a=B_a^m{\overline{e}}_m$，且有 $A^{-1}=B$，使用 index 进行表示则有：$AB=I$，或者 $A_m^a{B}_b^m={\delta }_b^a$

我们现在考虑张量的分量在改变基前后的变化。

考虑 $v=v^a{e}_a={\bar{v}}^a{\overline{e}}_a\in V$，那么有：

$$v^a=f^a(v)=f^a({\overline{v}}^b{\overline{e}}_b)={\overline{v}}^b{f}^a({\overline{e}}_b)={\overline{v}}^b{f}^a(A_b^m{e}_m)=A_b^m{\overline{v}}^b{f}^a(e_m)=A_b^a{\overline{v}}^b$$

考虑 $w=w_a{f}^a={\bar{w}}_a{\overline{f}}^a\in V\ast$，有：

$$w_a=w(e_a)=w(B_a^m{\overline{e}}_m)=B_a^{m}w({\overline{e}}_m)=B_a^m{\bar{w}}_b{\overline{f}}^b({\overline{e}}_m)=B_a^m{\bar{w}}_m$$

总结起来，对 $v\in V,w\in V^{\ast }$，基 ${\overline{e}}_a=A_a^b{e}_b$，我们有：

$$\begin{array}{cc}{v}^a=A_b^a{\overline{v}}^b& w_a=B_a^b{\bar{w}}_b\\ {\overline{v}}^a=B_b^a{v}^b& {\bar{w}}_a=A_a^b{w}_b\end{array}$$

考虑一个 tensor $T\in T_q^{p}V$，那么：

$$T_{b_1\cdots b_q}^{a_1\cdots a_p}=A_{m_1}^{a_1}\cdots A_{m_p}^{a_p}{B}_{b_1}^{n_1}\cdots B_{b_q}^{n_q}{\bar{T}}_{n_1\cdots n_q}^{m_1\cdots m_p}$$

根据我们之前定义 matrix 的操作，既然 matrix 是由我们的 convention 鼓捣出来的，那么自然可以鼓捣出 matrix 上的操作，比如一个 matrix 的 determinant(行列式)

problem

考虑一个张量 $\varphi \in T_1^{1}V$，那么我们可以将张量的分量 ${\varphi }_b^a$ 写成矩阵形式：

$$\varphi ={\varphi }_b^a{e}_a\otimes f^b\iff \varphi =\left(\begin{array}{cccc}{\varphi }_1^1& {\varphi }_2^1& \cdots & {\varphi }_d^1\\ {\varphi }_1^2& {\varphi }_2^2& \cdots & {\varphi }_d^2\\ ⋮& ⋮& \ddots & ⋮\\ {\varphi }_1^d& {\varphi }_2^d& \cdots & {\varphi }_d^d\end{array}\right)$$

类似的，如果我们有张量 $g\in T_2^{0}V$，其分量 $g_{ab}:=g(e_a,e_b)$，可以写为：

$$g=g_{ab}{f}^a\otimes f^b\iff g=\left(\begin{array}{cccc}{g}_{11}& g_{12}& \cdots & g_{1d}\\ g_{21}& g_{22}& \cdots & g_{2d}\\ ⋮& ⋮& \ddots & ⋮\\ g_{d1}& g_{d2}& \cdots & g_{dd}\end{array}\right)$$

显然这俩张量完全不同，其中 $\varphi$ 是 $End(V)$ 中的一个元素，而 $g$ 是一个 V 上的双线性形式，但是根据其矩阵形式描述，我们其实很难区分，这也是矩阵描述的一个缺点。

^example-matrix-flaw

总之回到原问题，我们在矩阵上有求行列式的操作，你可能会想这俩都有矩阵形式表述，是不是都可以做行列式操作呢？答案是否定的！我们只能对 ^def-endomorphism 进行这种操作，我们将给出原因：

考虑 M 是一个集合，称 M 的一个置换 (permutation) 是一个 $M\to M$ 的双射，进一步定义 n 阶对称群 (symmetric group of order n)，记为 $S_n$，是集合 $\left\{1,\cdots ,n\right\}$ 的置换的集合，其上附带了函数复合的操作作为运算 (来构成群)

我们称一个 transposition 是一个置换，其只改变 2 个元素，其他元素不变。那么我们有下面的结论：

任何置换 $\pi \in S_n$，可以被写成 $S_n$ 中 transposition 的复合

尽管一个置换 $\pi$ 的分解可能是不唯一的，但是其分解为 transposition 的数目则是要么为奇数要么偶数，是一个 $\pi$ 的不变量（否则就存在使用奇数次 transposition 回到原点的操作），从而我们可以定义一个关于 $\pi$ 的函数：

sgn

$$\text{sgn}\left(x\right):=\{\begin{array}{l}+1\\ -1\end{array}\{\begin{array}{l}\mathrm{if}N\left(\pi \right)\mathrm{is}\mathrm{even}\\ \mathrm{if}N\left(\pi \right)\mathrm{is}\mathrm{odd}\end{array}$$

其中 $N(\pi )$ 代表分解 $\pi$ 的 transpositions 的数量

^def-sgn

n-form

现在回到 tensor space，考虑 V 是一个 d 维向量空间，一个 n-form on V 是一个 $(0,n)$ 张量 $w$，且是完全反对称的 (totally antisymmetric)，即：

$$\forall \pi \in S_n:w(v_1,v_2,\cdots ,v_n)=sgn(\pi )w(v_{\pi (1)},v_{\pi (2)},\cdots ,v_{\pi (n)})$$

^def-n-form

注意到 0-form 是一个 scalar，1-form 是一个 covector，一个 d-form 也被称为一个 top-form。定义 n-form 还有一些别的方式，比如：

theorem

一个 $(0,n)$tensor w 被称为 n-form，当且仅当： 当 $\left\{v_1,\cdots ,v_n\right\}$ 是线性相关时， $w(v_1,\cdots ,v_n)=0$

上面的定理告诉我们，尽管我们可以定义 n>d 的 form，但其值只能是 0.

theorem

记 ${\Lambda }^{n}V$ 是 V 上 n-form 构成的向量空间，那么我们有：

$$dim{\Lambda }^{n}V=\{\begin{array}{ll}\left(\begin{array}{c}d\\ n\end{array}\right)& if1\le n\le d\\ 0& ifn>d\end{array}$$

其中

$$\left(\begin{array}{c}d\\ n\end{array}\right)=\frac{d!}{n!(n-d)!}$$

特别的，$dim{\Lambda }^{d}V=1$，这意味着：

$$\forall w,w^{\prime }\in {\Lambda }^{d}V:\exists c\in K:w=c{w}^{\prime }$$

即我们可以称只有一个 top form on V

definition

称一个 choice of top-form on V 是一个 choice of volume form on V，一个带有 chosen volume form 的向量空间被称为一个带有体积的向量空间 (vector space with volume)

^def-vector-space-with-volume

这一定义的有用之处在于下面定义：

考虑 $dimV=d$，取 $w\in {\Lambda }^{d}V$ 是一个 V 上的 volume form，那么给定 $v_1,\cdots ,v_d\in V$，可以定义 $v_1,\cdots ,v_d$ 扩充出的空间的 体积 为：

$$\text{vol}(v_1,\cdots ,v_d):=w(v_1,\cdots ,v_d)$$

直觉上来看，w 上的反对称性质保证了当 $\left\{v_1,\cdots ,v_d\right\}$ 是线性相关的时候，定义的体积为 0，这也是符合我们几何直觉的，因为线性相关的时候最多构成一个 V 上的 d-1 维超平面，体积为 0

remark

我们定义体积的时候似乎并没有要求V上的一些其余结构，比如长度、角度、内积啥的，我们唯一要求的是一个top form，其定义依赖于V是一个有限维拓扑流形

现在终于可以给出行列式在 tensor 意义下的定义了：

V 是一个 d 维向量空间，考虑 $\varphi \in End(V){\cong }_{\text{vec}}{T}_1^{1}V$，定义 $\varphi$ 的 determinant 为：

$$\det \varphi :=\frac{w(\varphi (e_1),\cdots ,\varphi (e_d))}{w(e_1,\cdots ,e_d)}$$

其中 $w\in {\Lambda }^{d}V$，$\left\{e_1,\cdots ,e_d\right\}$ 是 V 的一组基

我们首先检查是不是 well-defined，注意到 $\varphi$ 是不依赖于基选取的，也不依赖于 $w$ 选取的，可以验证，两个都是成立的。

从这里 determinant 的定义可以看出，其只能对 $T_1^{1}V$ 元素进行计算。

现在回顾我们研究的 2 个对象的定义：^example-matrix-flaw

可以发现，如果使用矩阵形式，进行转换基底操作，有：${\overline{e}}_a=A_a^b{e}_b$：

那么：

$${\varphi }_b^a=A_m^a{B}_b^n{\bar{\varphi }}_n^m\Rightarrow \varphi \to A^{-1}\bar{\varphi }A$$

对 g 有：

$$g_{ab}=B_a^m{B}_b^n{\bar{g}}_{mn}\Rightarrow g\to A^T\bar{g}A$$

如果按照矩阵方式计算其行列式，有：

$$\det (A^{-1}\varphi A)=\det (\varphi )$$

至少是和基底无关的；

考虑 (类似度量矩阵) 的 g，有：

$$\det (A^{T}gA)=\det (A{)}^2\det (g)$$

表明结果和基底有关，这不是一个 well-defined 的 object

但是我们之后将会遇见一个量 $X$，其具有下面变换性质：

$$X\to \frac{1}{\det (A{)}^2}X$$

这表明这一量 X 在换基作用下也不是 well-defined。但是如果结合起来有：

$$\det (g)X\to \cancel{\frac{\det (A{)}^2}{\det (A{)}^2}}\det (g)X=\det (g)X$$

这就是一个 well-defined 的 object 了。这一结果将在 principal fibre bundle 中遇见，使用这一结果，我们可以给 bundle 上定义 tensor，并给出 tensor densities，其直观上来讲是一种可以在换基变换下 随着 detA 的指数变化的量

参考

引文

• 为什么要定义张量积? - 知乎
• [前置内容] 从映射到张量 - 知乎
• 終 · 一步到位的张量指标运算 - 知乎

脚注

---

1. 双线性形式及其应用 ↩︎