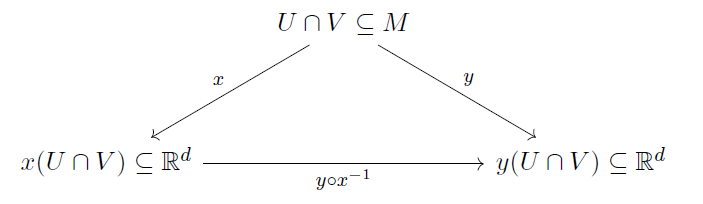Chap3 Topological manifolds and bundles
Chap3 Topological manifolds and bundles
拓扑流形和 Bundle
Manifold
manifold
一个 paracompact, Hausdorff 的拓扑空间 被称为 d-dimensional(topological) manifold 如果:
对 M 中任意点 ,存在一个邻域 还有一个同胚 (homeomorphism)。我们也表示为:
^def-manifold
直观上来看,一个 d 维拓扑流形指的是一个 (任意点) 局部类似于 的拓扑空间。
note
注意,我们目前实际上看到的是实拓扑流形,如果要考虑复的情形,只需要将同胚x改成映射到上的开集就可
theorem
考虑 M 是一个 d 维拓扑流形, 且是开的,相交的 。如果 x,y 是 2 个 homeomorphism,且:
那么
这个定理告诉我们,dimension 这个概念定义是没问题的,即 well-defined。它在任意一点 (任意连通的部分的一点) 上是相同的
类似定义子拓扑空间的思路,我们也可以定义子流形:
definition
是一个拓扑流形,,那么 被称为 的一个子流形 (如果它本身是一个流形)
^def-sub-manifold
一些简单的关于子流形的例子:
- 是 的子流形
- 是 的子流形
同样的,拓扑空间可以 product,那么拓扑流形也可以这么操作:
definition
和 是 2 个维数为 m 和 n 的流形,那么 是一个维数为 的流形
^def-product-manifold
举例来说,我们有:
- (可以证明其不仅是拓扑空间,还是拓扑流形);进一步: 是一个 n 维流形
- 是一个 2 维流形
Bundle
一点题外话,在 物理 中经常用到 Product 这个操作,直观上来看,两个流形的 product 可以看成在第一个流形的每一点上粘上另一个流形的复制,但是并不是所有的流形都可以看成流形的 prouct,一个经典的例子就是莫比乌斯环:很像是 但是被扭曲了一面,从而和圆柱完全不同
bundle
一个拓扑流形的 bundle 是一个三元组: 其中 E 和 M 是拓扑流形,分别记为 total space 和 base space, 是一个 连续的 满射 ,被称为 projection map
我们通常记 bundle 为
^def-bundle
fibre
bunlde,M 上存在一点 ,那么称 为在 p 点的 fibre
^def-fibre
直观上来看,在 p 点的 fibre 是 E 中 (通过映射 ) 连接到 p 点的点集 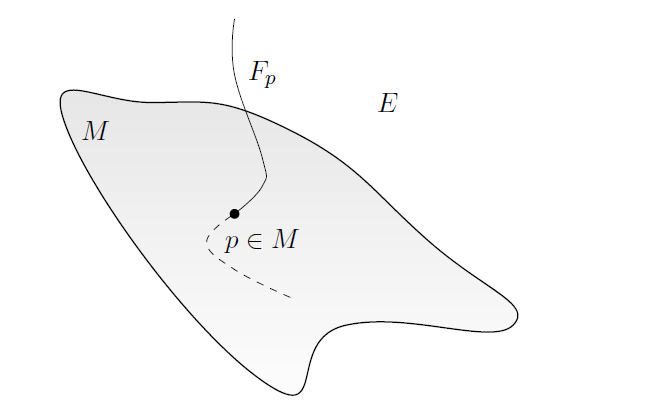
一个直观的 bundle 是 product bundle,可以通过 product manifold 构造:
从而得到 bundle
根据我们的定义,bundle 是比 product 更宽泛的结构,可以通过下面例子解释:
example
考虑 total space E 为莫比乌斯环,M 是 circle (),如下图示意:

其中这个矩形代表未折叠的莫比乌斯环,可以发现这是一个 bundle 但不是一个 product
^example-mobius-bundle
bunlde 可以具有更奇怪的结构,一个 manifold 上可以具有完全不同的 bundle:
example
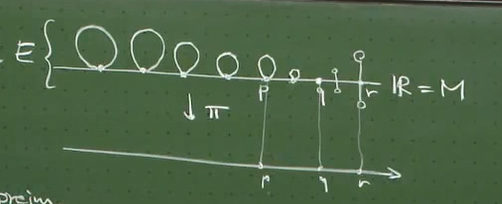
观察这个 bundle 对应的 fibre:
fibre bundle
是一个 bundle,F 是一个流形,那么称 是一个 fibre bundle(纤维丛),with (typical) fibre F,如果:
可以将一个纤维丛表示为:
^def-fibre-bundle
从定义上来看,这个定义直观上就是把 fibre 具象化出来,可以参考示例:
- 是一个 fibre bundle,with fibre
- 莫比乌斯带是一个 fibre bundle: ,其中
section
考虑 是一个 bundle,映射 是一个 (cross-)section of the bundle,如果:
^def-section
直观上来看,一个 section 是一个映射 可以将 base space 中的每个点 P 送到 E 中的纤维 上的某个点 处,从而有 可以通过 回到
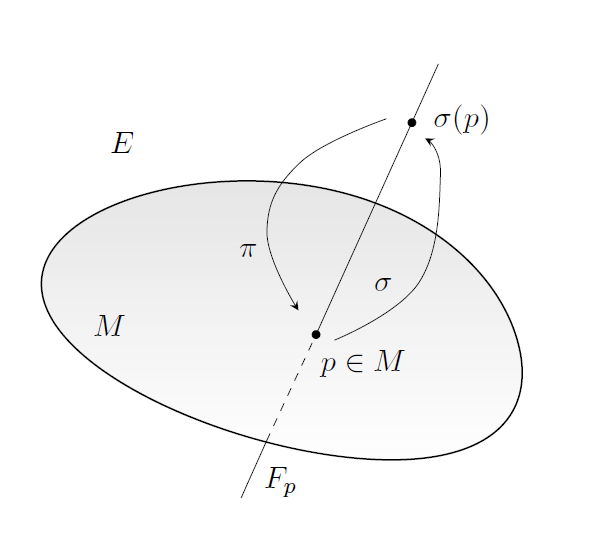
还是用最简单的 product bundle 来说明,考虑 product bundle ,那么这个 Bundle 的 section 是这样一个映射:
其中 是任意一个映射
在完成了 bundle 的定义后,考虑子流形上的 bundle:
sub-bundle
一个 bundle 的 sub-bundle 是一个三元组 ,其中 是子流形,
^def-sub-bundle
为了引出 bundle 之间的同构,我们补充定义 restricted bundle:
restricted bundle
一个 bundle , 是一个子流形,那么 restricted bundle (to N) 是一个三元组 其中:
^def-restricted-bundle
现在我们可以考虑 bundle 之间的同构了:
bundle morphism
有 和 是 bundle,考虑映射 和 ,称二元组 是一个 bundle morphism 下面的映射成立:
或者说:
^def-bundle-morphism
容易证明,如果存在 2 个 bundle morphism 和 ,那么 (但是 u 不一样似乎就没办法了)。这表明,如果 u 确定了,那么使得 (u,v) 是 Bundle morphism 的 v 是唯一的
在上面的 bundle morphism 基础上,我们可以构造 bundle 之间的同构 (isomorphism)
bundle isomorphism
两个 bundle 和 被称为 isomorohic(as bundles) 如果存在 bundle morphism 和 使得:
这样的 被称为 bundle isomorphism,我们记为:
^def-bundle-isomorphism
note
正如前面各种isomorphism所表示的,bundle isomorphism是对bundle保持结构不变的映射
全局的 isomorphic 可能要求比较苛刻,我们可以考虑局部的 isomorphic:
locally isomorohic
我们称一个 bundle 是 locally isomorohic (as a bundle) to a bundle ,如果对任意点 有邻域 使得 restricted bundle:
和 bundle 是 isomorphic 的
^def-locally-bundle-isomorphism
由于 product bundle 的简单性质,我们可以将与之 isomorphic 的 bundle 都提出来,记 bundle 是
- trivial,如果其和一个 product bundle 同构
- locally-trivial,如果和 product bundle locally isomorphic
可以发现,我们之前定义的 莫比乌斯映射 是 locally trivial 的但不是 trivial 的,而 Cylinder C 则是 trivial 的
note
在我们的应用种,我们一般考虑的是locally trivial bundles
pull-back bundle
考虑 是一个 bundle,f 是从一个流形 M’出发的映射,。定义从 bundle 使用 映射 f 诱导出的 pull-back bundle: :
且
^def-pull-back-bundle
从定义中可以看出来,这就是一个 product bundle 的形式,我们可以很轻松的构建出 bundle morphism:
其中 就是一个投影映射:
注意到我们构造的 pull-back bundle 是 trivial 的 product bundle,从而我们可以很容易的得到其上的 section 的形式,如下 式子 所示:
^eqn-pull-back-bundle-section
其中 和 都是二元组 的 projection 映射。对 bundle 上的 section ,考虑映射 ,其构成了一个 到 的映射。注意到:
根据 ^def-pull-back-bundle 的 的构造定义,,而又考虑到我们构造的 ,从而在 pull-back bundle 上的 section 可以直接构造为:
显然其满足 section 的定义,且也满足
Atlas & Manifold
chart of manifold
是一个 d 维流形,称一个 pair 是该 Manifold 的 chart,其中 , 是一个 homeomorphism
称component functions(maps) of 为:
其中,而是的第i个分量。我们称为点针对chart 的co-ordinates(坐标)
^def-chart-of-manifold
在全局意义上我们可以将 chart 收集起来,从而得到了 Atlas
atlas
一个流形 M 的 atlas 是一个 chart 的集合:
且满足:
^def-atlas
显然不同的 chart 之间会有 overlap,在 Overlap 中的点在不同的 chart 下会有不同的坐标,这就是我们希望研究的:
^def-C0-compatible
注意到映射 x, y 都是 homeomorphism,那么复合映射 也是 homorphism,从而必定是 continuous 的,这意味着一个流形上的任意 2 个 chart 都是 C0-compatible 的
我们称一个流形上的 是所有 C0-compatible 的 chart 的集合,那么任何 atlas 都是 C0-atlas
从名字就可以看出来,后面还会有 Ck-compatible 这类的定义 (实际上就是 differentiability)
我们称一个 C0-atlas 是一个 maximal atlas 如果:对任意 chart ,我们有:所有的和 C0-compatible 的 chart 都属于 ,即 。 ^c172db
显然,不是所有的 C0-atlas 都是 maximal atlas,比如考虑流形 ,atlas 为 ,那么这就不是一个 maximal atlas,因为考虑 chart 是和 C0-compatible 的,但是并不在 中
在有了 atlas 之后,我们终于可以跳出 manifold 观察物体了,现在分析问题就可以从 manifold 上或者利用 atlas 从 上分析了。举例来说,考虑研究一个 curve 是否为连续的:
- 从 manifold 上,我们有以往的定义,即 curve 是否为连续的依赖于映射 是否是从拓扑空间 到拓扑空间 的连续的映射
- 使用 atlas 可以有我们更加熟悉的结果:
我们首先考虑空间 M 的一个开子集,并将映射 替换,考虑复合映射:
现在我们更希望直接 check 新的欧式空间 上的曲线是不是连续的,即每个分量的连续性。
这么做把问题转换到了熟悉的欧式空间中,方便我们计算,但也存在问题:如果选取了 2 个 chart 怎么办?
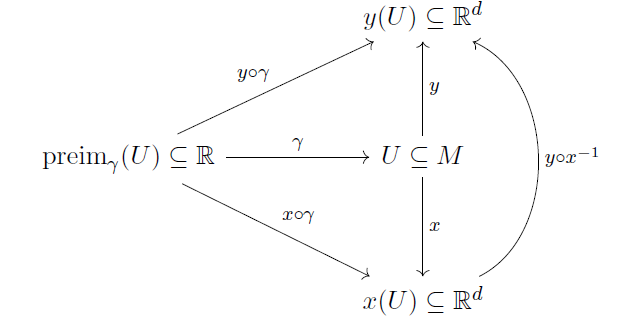
Chap3 Topological manifolds and bundles 2022-09-04 11
如上图,可以使用简单的映射完成转换。更“抽象”地说,映射 实际上允许我们不依赖原流形 M 的结构 (比如 U, x, y) 来考虑问题,因为实际上这是 之间的 映射。