求解ODE
2022年6月6日
求解ODE
求解 ODE
定义
使用计算机方法求解一个 ODE 方程
可以得到解析解情形
对可以手算得到 ODE 方程的解析解的情形,没什么好说的
Mma
使用 Mathematica 符号计算 (DSolve) 求解 ODE 的解析解,效果挺好.
比如求解
显然手解是不方便的
没有解析解,尝试数值解
Mma
数值解最先使用 Mathematica 尝试求解,因为定义简单方便,求解范围广。 这里的求解范围广包括边界条件类型广,从简单的数值边界条件到 BVP(Boundary value problem, 即边界为数值情况的符号等式,比如 y(start)=a y(end)),再到 Neumann 情形的边界条件 (类似 PDE 定义,比如 y'(start)=a y(end)+b)。
一个直观的例子是李家聪提出的,求解大变形的球面应力 - 变形映射关系,问题如下:
具体问题形式为:
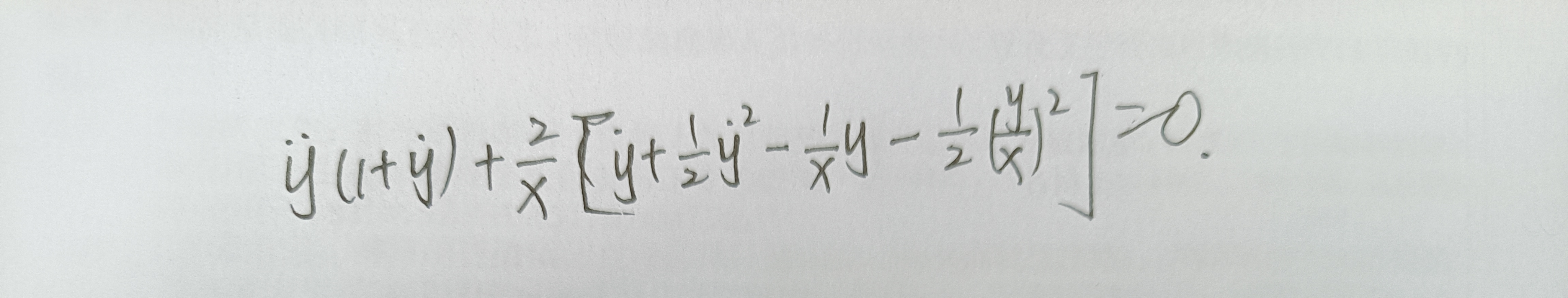
求解代码参考:
xstart = 0.01;
xend = 1;
ic = {y'[xstart] == -5 y[xstart] + 3, y'[xend] == y[xend]}
nsol = NDSolve[{eqn, ic}, y, {x, xstart, xend}]
Plot[Evaluate[y[x] /. nsol], {x, xstart, xend}]
Matlab
matlab 求 ODE 数值解从基本问题到 BVP 都有包可以调用,但对复杂的 Neumann 似乎没办法,可以参考下面文章求解:
- pde - Implementation of Neumann boundary condition with method of lines - 1D diffusion/reaction equation - Computational Science Stack Exchange
- amath.kaist.ac.kr/pde_lab/members/JaywanChung/MatlabLecture.pdf
Julia
等我学会了 julia 再填坑,但我觉得应该是可以的。
参考
Loading...