chap11 弯曲应力

chap11 弯曲应力

基本介绍

在上一章说明了一般情况下，梁内同时存在剪力和弯矩；因此在梁的横截面上，将同时存在切应力和正应力。

只有切向微内力 $\tau \mathrm{d}A$ 可能构成剪力；只有法向微内力 $\sigma \mathrm{d}A$ 才可能构成弯矩；对应的，梁弯曲时横截面上的切应力和正应力，分别称为 弯曲切应力 和 弯曲正应力

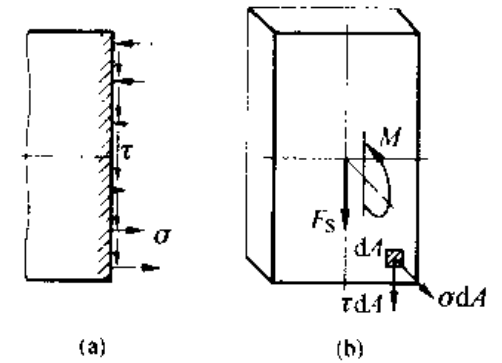
前面介绍，弯曲、扭转和轴向拉压是杆件变形的三种基本形式。

在机械工程中，最常见的梁往往至少具有一个纵向对称面，外力则作用在该对称面内；这种情况下，梁的变形对称于纵向对称面=>对称弯曲

对称弯曲正应力

基本假设

取一根对称截面梁，在其侧表面画上纵线和横线；在梁两端纵向对称面内，施加一对方向相反，力偶矩均为 M 的力偶，使得梁处于纯弯曲状态。实验中观察到：

• 梁侧表面的横线仍为直线，且与纵线正交，只是横线之间做相对转动
• 纵线变为弧线，并且在靠近梁顶面的纵线缩短时，靠近梁地面的纵线伸长
• 在纵线伸长区，梁的宽度减小；反之亦然

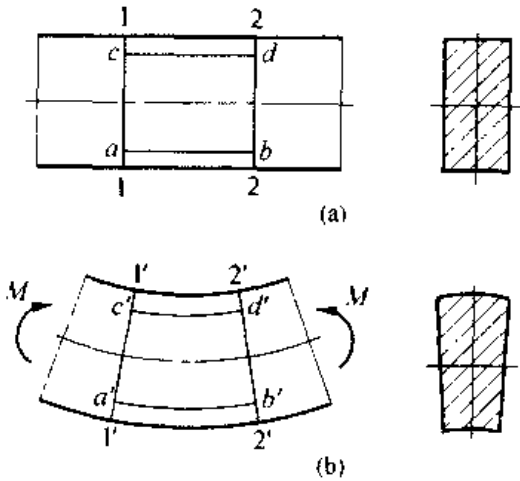
根据上面现象，对梁内受力和变形做下面假设：

• 变形后，横截面仍保持平面，且和纵线正交：弯曲平面假设
• 梁内各个纵向“纤维”仅仅承受轴向拉应力或者压应力：单向受力假设

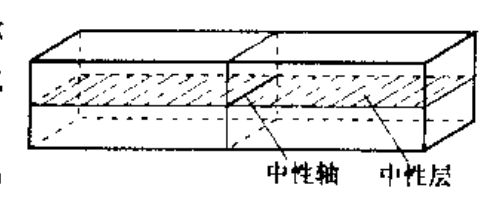
根据平面假设，可以发现，在纵向“纤维”伸长和缩短区域存在一个长度不变的过渡层：中性层

中性层和截面的交线是中性轴；纯弯曲时梁的所有横截面仍然保持平面，且绕着中性轴做相对转动；所有纵向纤维均处于单向受力状态

弯曲应力分析

为了建立应力分析方程，从几何、物理、静力学三方面进行分析

几何方面

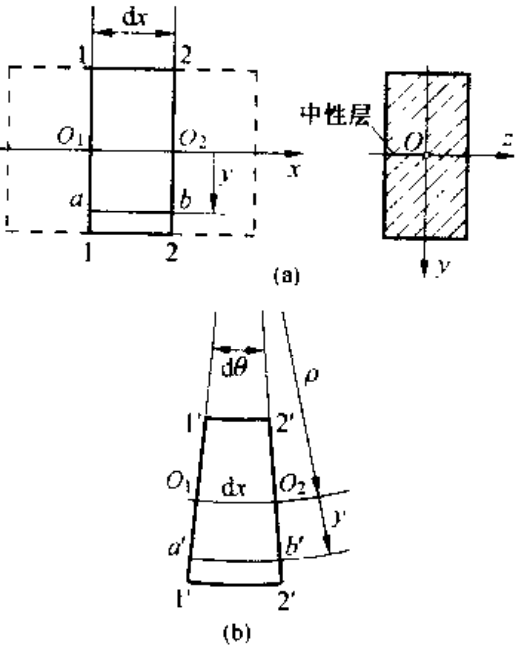
首先分析纵向“纤维”的变形；如上图建立坐标系。

纵线 ab 的正应变为：

$$\epsilon =\frac{a^{\prime }{b}^{\prime }-ab}{ab}=\frac{y\mathrm{d}\theta }{\rho \mathrm{d}\theta }=\frac{y}{\rho }$$

这表明了，距离中心层纵坐标 y 的任一纤维的正应变

物理方面

由于上面假设有单项受力条件，因此，在正应力不超过材料的比例极限时，可以使用胡克定律有：

$$\sigma =E\epsilon =E\frac{y}{\rho }$$

静力学方面

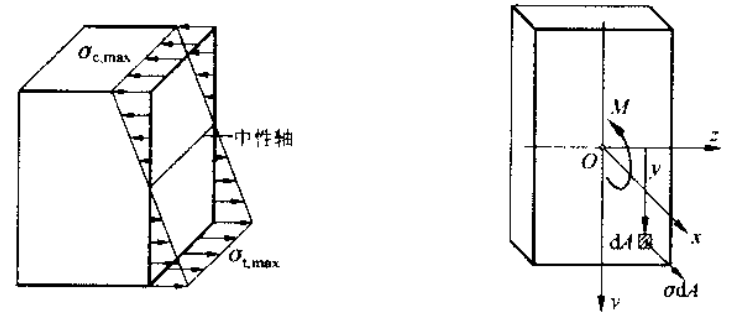
考虑静力学条件，建立静力学方程有：

• 横截面无轴力
• 横截面仅存在 x-y 平面的弯矩

$$\{\begin{array}{c}{\int }_A\sigma \mathrm{d}A=0\\ {\int }_{A}y\sigma \mathrm{d}A=M\end{array}\Rightarrow \{\begin{array}{c}{\int }_{A}E\frac{y}{\rho }\mathrm{d}A=0\\ {\int }_{A}yE\frac{y}{\rho }\mathrm{d}A=M\end{array}$$

根据形心的定义，截面形心 C 的纵坐标为：

$$y_c=\frac{{\int }_{A}y\mathrm{d}A}{A}=0$$

因此中性轴通过截面形心。

此外，定义类似极惯性矩有，定义惯性矩 $I_z$ 为截面对 z 轴的惯性矩 (这里 z 轴是中性轴)

$$I_z={\int }_A{y}^2\mathrm{d}A$$

因此对弯矩方程有：

$$\begin{gathered} \frac{E}{\rho }{\int }_A{y}^2\mathrm{d}A=\frac{E}{\rho }{I}_z=M \\ \Rightarrow \frac{1}{\rho }=\frac{M}{E{I}_z} \end{gathered}$$

注意到，中性层的曲率 $1/\rho$ 和弯矩 M 成正比，与 $E{I}_z$ 成反比；其中 $E{I}_z$ 被称为 弯曲刚度。进一步可以得到，截面 y 上的正应力为：

$$\sigma =E\epsilon =E\frac{y}{\rho }=\frac{My}{I_z}$$

使用上面正应力公式，可知在横截面上距离中心轴最远的点有最大的弯曲正应力，定义：

$$W_z=\frac{I_z}{y_{\max }}$$

为 抗弯截面系数。

惯性矩和平行轴定理

基本截面惯性矩

截面类型	截面形状	惯性矩
矩形截面		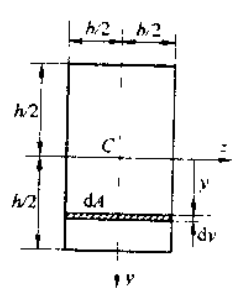$I_z=\frac{b{h}^3}{12},W_z=\frac{b{h}^2}{6}$
圆形截面		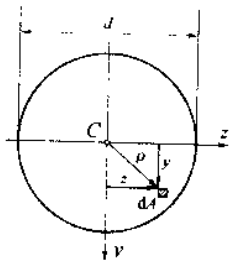$I_z=\frac{\pi d^4}{64},W_z=\frac{\pi d^3}{32}$
空心圆截面	NA	$I_z=\frac{\pi D^4}{64}\left(1-{\alpha }^4\right),W_z=\frac{\pi D^3}{32}\left(1-{\alpha }^4\right)$

平行轴定理

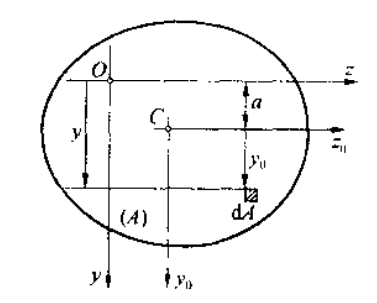
z0 轴是形心轴，z 和 z0 轴平行，相距为 a，截面对 z 轴的惯性矩为：

$$I_z={\int }_A{y_0}^2\mathrm{d}A+2a{\int }_A{y}_0\mathrm{d}A+A{a}^2=I_{z_0}+A{a}^2$$

其中 z0 是形心轴保证第二项为 0.

对称弯曲切应力

当梁非纯弯曲时，横截面上除了正应力，还存在切应力，也就是 弯曲切应力。

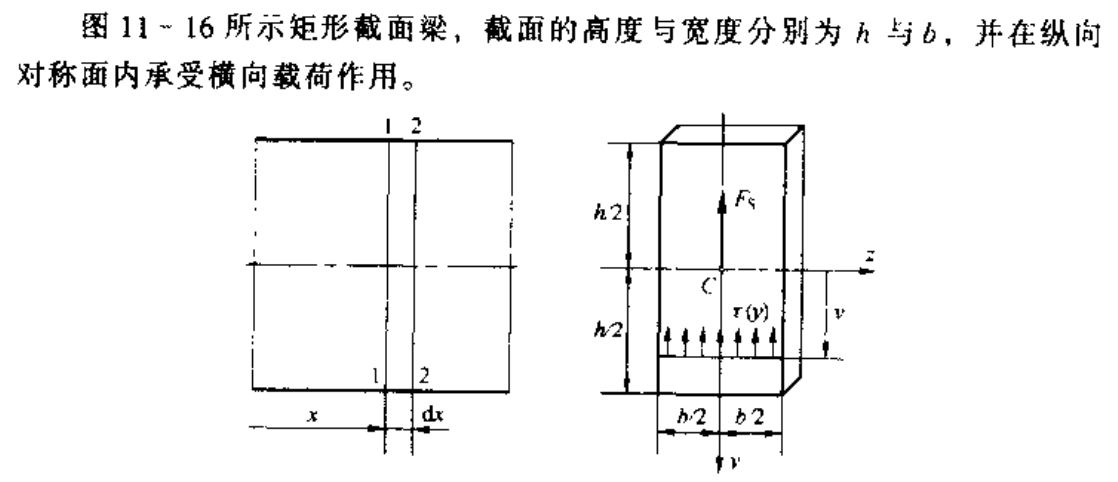
• 考虑到切应力互等定理，在梁表面没有轴向切应力 (y 轴方向)，那么横截面边缘不存在垂直于截面边缘的切应力 (z 轴方向)，因此截面切应力应该平行于截面周边。

• 如果界面是窄高的，可以认为在截面的宽度方向，切应力的大小和方向不显著变化

因此可以得到下面假设：

横截面上个点的切应力，均平行于剪力或者截面侧边，且沿着截面宽度均匀分布

使用微元法分析切应力关系：

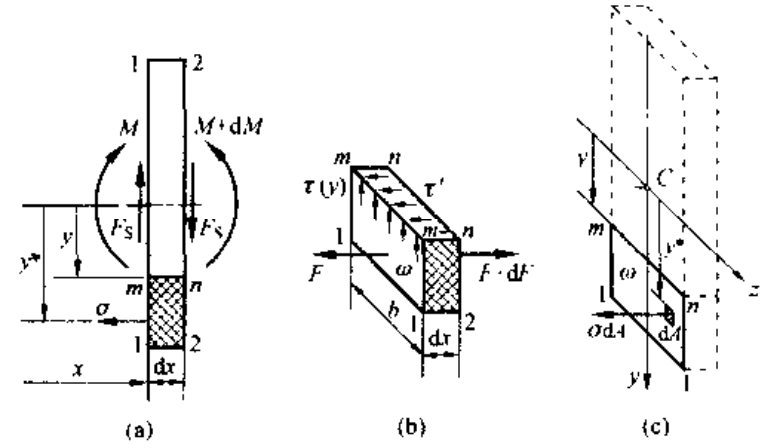
建立力平衡方程：

$$\tau \left(y\right)b\mathrm{d}x=\mathrm{d}F\Rightarrow \tau \left(y\right)=\frac{1}{b}\frac{\mathrm{d}F}{\mathrm{d}x}$$

注意到：

$$F={\int }_{\omega }\sigma \mathrm{d}A={\int }_{\omega }\frac{My}{I_z}\mathrm{d}A=\frac{M{S}_x\left(\omega \right)}{I_z}$$

其中 $S_x\left(\omega \right)={\int }_{\omega }y\mathrm{d}A$，代表截面 w 对 z 轴的静矩。带入有：

$$\tau \left(y\right)=\frac{1}{b}\frac{\mathrm{d}F}{\mathrm{d}x}=\frac{1}{b}\frac{S_x\left(\omega \right)}{I_z}{F}_S$$

其中对一个矩形截面，有：

$$I_z=\frac{b{h}^3}{12},S_x\left(\omega \right)=\frac{b}{2}\left(\frac{h^2}{4}-y^2\right)$$

得到的剪力分布为：

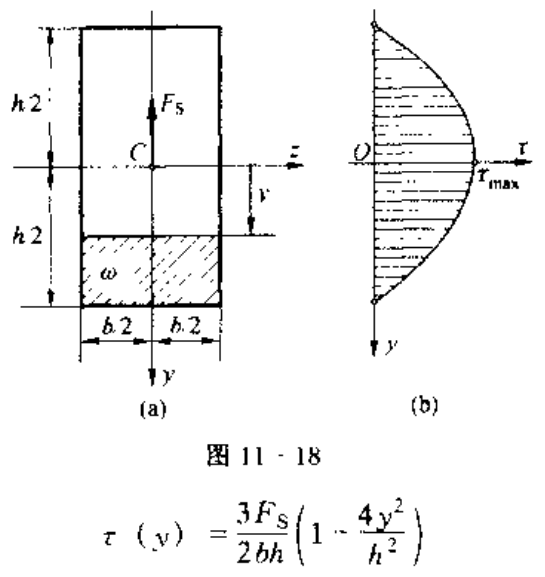
这表明：矩形截面梁的弯曲切应力沿着截面高度的分布是非均匀的，从而切应变沿着截面高度分布也不均匀。

对于工字钢的切应力分布计算，可以参考书 P226

---

注意到，对弯曲正应力和弯曲切应力，一下图为例：

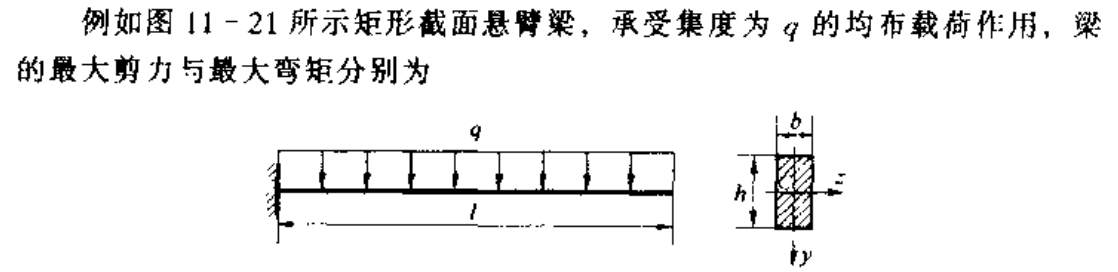
其最大剪力和最大弯矩分比为：

$$F_{S,\max }=ql,|M{|}_{\max }=\frac{q{l}^2}{2}$$

从而最大弯曲正应力和最大弯曲切应力为：

$$\begin{gathered} {\sigma }_{\max }=\frac{|M{|}_{\max }}{W_z}=\frac{3q{l}^2}{b{h}^2} \\ {\tau }_{\max }=\frac{3F_{S,\max }}{2A}=\frac{3ql}{2bh} \end{gathered}$$

因此二者比值为：

$$\frac{{\sigma }_{\max }}{{\tau }_{\max }}=2\frac{l}{h}$$

当梁的跨度 l 远大于截面高度 h 时，梁的最大弯曲正应力远大于最大弯曲切应力

类似于拉压杆和扭转杆，梁也有定义强度条件：

• 弯曲正应力强度条件：${\sigma }_{\max }={\left(\frac{M}{W_z}\right)}_{\max }⩽\left[\sigma \right]$
• 弯曲切应力强度条件：${\tau }_{\max }={\left(\frac{F_S{S}_x}{I_z\delta }\right)}_{\max }⩽\left[\tau \right]$

非对称弯曲

Too complicated...Ref to 《弹性力学》