分析力学

分析力学

虚功原理

我们从一个 N 体质点系统开始，约定：$m_i$ 代表每个支点质量，$r_i(i=1,2,\cdots ,N)$ 代表支点位移。根据 变分 的原理，举例有：在如下的约束下：

$$f(x_1,y_1,z_1,\cdots ,z_N,t)=C$$

有虚位移满足：

$$f(x_1+\delta x_1,y_1+\delta y_1,z_1+\delta z_1,\cdots ,z_N+\delta z_N,t)=C$$

使用 Taylor 展开有：

$$f\left(x_1,y_1,z_1,\dots ,z_N,t\right)+\sum _{i=1}^N\left(\frac{\partial f}{\partial x_i}\delta x_i+\frac{\partial f}{\partial y_i}\delta y_i+\frac{\partial f}{\partial z_i}\delta z_i\right)+O\left({\delta }^2\right)=C$$

进而得到了：

$$\sum _{i=1}^N\left(\frac{\partial f}{\partial x_i}\delta x_i+\frac{\partial f}{\partial y_i}\delta y_i+\frac{\partial f}{\partial z_i}\delta z_i\right)=0$$

^54a7d8

这意味着 3N 个虚位移中只有 3N-1 是任意的 (无关的)，因此有效的虚位移和系统的约束有关，和系统的自由度相同。

回到原问题，取和系统自由度一样多的虚位移 $\delta r_i$。对于静平衡的系统而言，假设该 N 体系统受到一系列合成后的力 $R_i(i=1,2,...N)$ 影响。为了系统静平衡，有对应的 $R_i=0$，进而对应的系统虚功有：

$$\overline{\delta W_i}=R_i\dot{\delta }{r}_i=0$$

其中 $\overline{\delta W_i}$ 被定义为系统在虚位移 $\delta r_i$ 和合成力 $R_i$ 作用下的虚功。

note

collapse: open title: Note 需要注意的是，这里的符号$\overline{\delta W_i}$这样写有两方面考虑：

• 符号$\delta$代表力作用在虚位移上，并不实际存在
• \overline 代表这并不是$W_i$的变分

考虑到系统在约束下，可以将合成力 $R_i$ 写为：$R_i=F_i+f_i$，其中 $F_i$ 为系统内力，$f_i$ 为约束力。

考虑到系统可能的虚位移向量存在于系统约束曲面的切空间中 (也就是虚位移向量一定和约束力垂直，不难通过上面关于 约束的微分 发现)，因此

$$\sum _{i=1}^N{f}_i\delta r_i=0$$

进一步有：

$$\sum _{i=1}^N{F}_i\delta r_i=0$$

note

collapse: open title: Note

需要注意这里的合成力乘虚位移为0，只有在力是保守力情况下才成立。当存在摩擦力的时候，狮子并不成立。因为虚位移存在的特性是可逆性，即取当前方向的反方向理论上也是可以的，但在这一情况下摩擦力会也反向，带来做功，因此力必须要为保守力。

可以表述为：在无穷小的可逆的满足系统约束的虚位移下，作用在该系统上的力做的功为 0

此外，考虑到一般性，将虚位移 $r_i$ 在选取的广义坐标 $q_k$ 上分解 (或者看成对 $r(q_1,q2,\cdots ,q_n)$ 上做 变分)，有：

$$\delta r_i=\sum _{k=1}^n\frac{\partial r_i}{\partial q_k}\delta q_k$$

因此可以得到在广义坐标上，有：

$$\sum _{i=1}^N{\mathbf{F}}_i\cdot \delta {\mathbf{r}}_i=\sum _{i=1}^N{\mathbf{F}}_i\cdot \sum _{k=1}^n\frac{\partial {\mathbf{r}}_i}{\partial q_k}\delta q_k=\sum _{k=1}^n\left(\sum _{i=1}^N{\mathbf{F}}_i\cdot \frac{\partial {\mathbf{r}}_i}{\partial q_k}\right)\delta q_k=\sum _{k=1}^n{Q}_k\delta q_k=0$$

因此有：

$$Q_k=\sum _{i=1}^N{\mathbf{F}}_i\cdot \frac{\partial {\mathbf{r}}_i}{\partial q_k}=0,(k=1,2,\cdots ,n)$$

D'Alembert Principle

对 虚功原理 的 N 体质点系，通过虚功原理分析了系统静平衡的受力情况。自然的，在考虑系统运动后，结合牛顿第二定律，对每个质点有：

$$F_i+f_i-m_i\ddot{r_i}=0$$

其中 $F_i$ 是施加在质点上的力，$f_i$ 是约束力。上式也被称为 d'Alembert principle，其中 $-m_i\ddot{r_i}$ 也叫做惯性力。

将上面的虚功定理由静平衡形式延伸到动态形式：

$$\sum _{i=1}^N(F_i+f_i-m_i\ddot{r_i})\delta r_i=0$$

同样的，其中不能存在摩擦力等等保守力，下面所有的讨论都基于理想的无摩擦的情形。

Hamilton Principle

我们知道：虚功定义为：

$$\sum _{i=1}^N{F}_i\delta r_i=\overline{\delta W}$$

，假定每个质点质量不变，有：

$$\begin{array}{rl}\frac{d}{dt}\left(m_i{\dot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i\right)& =m_i{\ddot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i+m_i{\dot{\mathbf{r}}}_i\cdot \delta {\dot{\mathbf{r}}}_i=m_i{\ddot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i+\delta \left(\frac{1}{2}{m}_i{\dot{\mathbf{r}}}_i\cdot {\dot{\mathbf{r}}}_i\right)\\ & =m_i{\ddot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i+\delta T_i\end{array}$$

其中 $\delta T_i$ 代表质点的动能，因此有：

$$\sum _{i=1}^N\frac{d}{dt}\left(m_i{\dot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i\right)=\sum _{i=1}^N{m}_i{\ddot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i+\delta T$$

注意到约束力和虚位移垂直，因此结合 D'Alembert Principle 有：

$$\delta T+\overline{\delta W}=\sum _{i=1}^N\frac{d}{dt}\left(m_i{\dot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i\right)$$

进一步对时间积分有：

$${\int }_{t_1}^{t_2}(\delta T+\overline{\delta W})dt={\int }_{t_1}^{t_2}\sum _{i=1}^N\frac{d}{dt}\left(m_i{\dot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i\right)dt={\sum _{i=1}^N{m}_i{\dot{\mathbf{r}}}_i\cdot \delta {\mathbf{r}}_i|}_{t_1}^{t_2}$$

在所有的虚位移中，我们只考虑那些正好能够在时刻 t1,t2 和原始正确轨迹重合的情形，因此有：

$${\int }_{t_1}^{t_2}(\delta T+\overline{\delta W})dt=0,\delta r_i(t_1)=\delta r_i(t_2)=0$$

![](assets/Pasted%20image%2020210812202953.png]]

考虑到广义坐标和原始使用的笛卡尔空间的坐标之间的转换关系隐含在 $\delta T,\overline{\delta W}$ 中，因此自然的得到了：

$${\int }_{t_1}^{t_2}(\delta T+\overline{\delta W})dt=0,\delta q_i(t_1)=\delta q_i(t_2)=0$$

note

collapse: open title: Note 注意这里没有如前面虚功原理和D'Alembert一样对所有质点的任意虚位移上之和为0，而这正是非保守力会在虚位移上产生问题？因此这里导出的方程是可以应用在任何情况下的？ #todo #notsure

一般来说，可以将虚功 $\overline{\delta W}$ 分解成保守力的功和非保守力的功，即：

$$\overline{\delta W}=\overline{\delta W_c}+\overline{\delta W_{nc}}$$

而对于保守力的虚功，我们可以知道其能够转换成使能的形式 (不如说本身就是势能的一种体现)，因此：

$$\overline{\delta W_c}=\delta W_c=-\delta V$$

进一步选取拉格朗日量 $L=T-V$，因此的得到：

$${\int }_{t_1}^{t_2}(\delta L+\overline{\delta W_{nc}})dt=0,\delta q_i(t_1)=\delta q_i(t_2)=0$$

在不存在非保守力的情形，有：

$${\int }_{t_1}^{t_2}\delta Ldt=0,\delta q_i(t_1)=\delta q_i(t_2)=0$$

注意到，对约束方程涉及到的坐标，如果约束方程的形式中对每个坐标都是单独出现的，即不存在类似 $q_1\cdot q_2$ 的形式，认为这个系统是 _ 可积的 _。对于这样的可积系统，真实路径是包含在虚位移空间中的。

如果约束条件中引入了速度，那么系统一定是不可积的。对于这样的不可积系统，真实路径一般来说不属于虚位移空间。

对可积的系统，变分 和积分是可以交换的，因此有：

$$\delta I=\delta {\int }_{t_1}^{t_2}Ldt=0,\delta q_i(t_1)=\delta q_i(t_2)=0$$

这个式子体现的是大家常见到的哈密顿原理形式。可以将其表述为：

对真实路径属于虚位移构成的位形空间的系统，假定在 t1,t2 时刻处虚位移为 0，在时间 t1,t2 之间，积分 $I={\int }_{t_1}^{t_2}Ldt$ 对所有虚位移保持恒定。

拉格朗日方程

在 Hamilton Principle 的基础上，为了进一步导出关于速度的微分方程，我们有名义上的 2 步需要考虑：

• 消除广义的虚位移速度，在积分号下仅仅保留虚位移项
• 利用虚位移任意的特性，使其对应系数为 0 来导出运动方程

Step 1

对系统的动能 T，可以将其表示为下面的一般形式：

$$T=T(q_1,q_2,\cdots ,q_N,\dot{q_1},\dot{q_2},\cdots ,\dot{q_N})$$

因此取 变分 有：

$$\delta T=\sum _{k=1}^n(\frac{\partial T}{\partial q_k}\delta q_k+\frac{\partial T}{\partial \dot{q_k}}\delta \dot{q_k})$$

而由于虚功 W，其在广义坐标下可以表示为：

$$\overline{\delta W}=\sum _{k=1}^n{Q}_k\delta q_k$$

其中 $Q_k$ 是作用在支点上外力在广义坐标上的投影。

因此根据 Hamilton Principle 有：

$$\begin{array}{c}{\int }_{t_1}^{t_2}(\delta T+\overline{\delta W})dt={\int }_{t_1}^{t_2}{\sum }_{k=1}^n\left[\frac{\partial T}{\partial {\dot{q}}_k}\delta {\dot{q}}_k+\left(\frac{\partial T}{\partial q_k}+Q_k\right)\delta q_k\right]dt=0,\\ \delta q_k\left(t_1\right)=\delta q_k\left(t_2\right)=0,k=1,2,\dots ,n\end{array}$$

对速度的 变分 项，考虑到性质：

$$\begin{array}{rl}{\int }_{t_1}^{t_2}\frac{\partial T}{\partial {\dot{q}}_k}\delta {\dot{q}}_{k}dt& ={\int }_{t_1}^{t_2}\frac{\partial T}{\partial {\dot{q}}_k}\frac{d}{dt}\delta q_{k}dt={\frac{\partial T}{\partial {\dot{q}}_k}\delta q_k|}_{t_1}^{t_2}-{\int }_{t_1}^{t_2}\frac{d}{dt}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)\delta q_{k}dt\\ & =-{\int }_{t_1}^{t_2}\frac{d}{dt}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)\delta q_{k}dt,k=1,2,\dots ,n\end{array}$$

因此有：

$${\int }_{t_1}^{t_2}\sum _{k=1}^n\left[-\frac{d}{dt}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)+\frac{\partial T}{\partial q_k}+Q_k\right]\delta q_{k}dt=0$$

Step 2

为了消除虚位移带来的不确定性保证上式成立，有系数为 0：

$$\frac{d}{dt}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)-\frac{\partial T}{\partial q_k}=Q_k$$

上式被称为 Lagrange's equations of motion (in their most general form)，其中 $Q_k$ 包含了保守力和非保守力。

进一步，为了取消保守力的作用，有：

$$Q_k=Q_{kc}+Q_{knc}$$

其中：

$$\delta W_c=-\delta V=-\sum _{k=1}^n\frac{\partial V}{\partial q_k}\delta q_k=\sum _{k=1}^n{Q}_{kc}\delta q_k$$

因此：

$$Q_{kc}=-\frac{\partial V}{\partial q_k}$$

即有：

$$\frac{d}{dt}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)-\frac{\partial T}{\partial q_k}+\frac{\partial V}{\partial q_k}=Q_{knc}$$

由于势能 V 中不包含速度项，因此取拉格朗日量有：

$$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_k}\right)-\frac{\partial L}{\partial q_k}=Q_{knc},L=T-V$$

可以发现，拉格朗日可以导出系统自由度同样多的微分方程，能够解出系统的状态。

哈密顿方程

拉格朗日方程 中包含了 n 个 2 阶微分方程，但对于数值求解来说，希望将其转换为 2n 个 1 阶微分方程更加习惯，这导出了我们的进一步思考。

注意到，我们可以使用类似状态方程的手段得到这 2n 个方程，具体来说就是把速度和位移分开成为 2 个变量。

因此，我们定义在广义坐标 $q_k$ 下的广义动量 $p_k=\frac{\partial L}{\partial \dot{q_k}}$，这一项用来对拉格朗日方程中速度项进行小区代替。

对于系统拉格朗日量，可以将其表示为： ^1cddfa

$$L=L(q_1,q_2,\cdots ,q_n,\dot{q_1},\dot{q_2},\cdots ,\dot{q_n},t)$$

进一步我们定义哈密顿函数 (Hamiltonian function) 为：

$$\mathcal{H}=\sum _{k=1}^n\frac{\partial L}{\partial {\dot{q}}_k}{\dot{q}}_k-L=\sum _{k=1}^n{p}_k{\dot{q}}_k-L$$

将 $\mathcal{H}$ 写为广义函数形式：

$$\mathcal{H}=\mathcal{H}(q_1,q_2,\cdots ,q_n,p_1,p_2,\cdots ,p_n,t)$$

对式子 哈密顿函数定义 进行 变分 有：

$$\begin{array}{rl}\delta \mathcal{H}& =\sum _{k=1}^n\left(p_k\delta {\dot{q}}_k+{\dot{q}}_k\delta p_k-\frac{\partial L}{\partial q_k}\delta q_k-\frac{\partial L}{\partial {\dot{q}}_k}\delta {\dot{q}}_k\right)\\ & =\sum _{k=1}^n\left({\dot{q}}_k\delta p_k-\frac{\partial L}{\partial q_k}\delta q_k\right)\\ \delta \mathcal{H}& =\sum _{k=1}^n\left(\frac{\partial \mathcal{H}}{\partial q_k}\delta q_k+\frac{\partial \mathcal{H}}{\partial p_k}\delta p_k\right)\end{array}$$

因此可以得到：

$$\dot{q_k}=\frac{\partial \mathcal{H}}{\partial p_k},-\frac{\partial L}{\partial q_k}=\frac{\partial \mathcal{H}}{\partial q_k}$$

考虑到之前得到的拉格朗日方程，有：

$$\dot{q_k}=\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_k}\right)=\frac{\partial L}{\partial q_k}+Q_{knc}$$

有：

$$\frac{\partial L}{\partial q_k}=\dot{q_k}-Q_{knc}$$

因此得到了一组微分方程：

$$\begin{array}{l}{\dot{q}}_k=\frac{\partial \mathcal{H}}{\partial p_k},k=1,2,\dots ,n\\ {\dot{p}}_k=-\frac{\partial \mathcal{H}}{\partial q_k}+Q_{knc},k=1,2,\dots ,n\end{array}$$

上式得到的 2n 个方程也被称为哈密顿方程 (Hamilton's equations)

对于式子 哈密顿函数定义，将其对时间微分，结合上面的微分方程可以发现：

$$\frac{\partial \mathcal{H}}{\partial t}=-\frac{\partial L}{\partial t}$$

显然的，如果拉格朗日量不显示的依赖于时间，那么哈密顿量也一样。

为了更加清晰的考虑问题，我们将哈密顿量和系统的动能、势能联系起来。

对于 n 自由度的系统而言，可以把其动能 $T$ 表示为：

$$T=T_2+T_1+T_0$$

其中：

$$T_2=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{m}_{ij}\dot{q_i}\dot{q_j}$$

这是一个二次型结构，反映的是系统的动能。

$$T_1=\sum _{j=1}^n{f}_j\dot{q_j}$$

是关于速度呈线性关系的，其中 $f_j=f_j(q_1,q_2,\cdots ,q_n)$ 为其系数。

$$T_0=T_0(q_1,q_2,\cdots ,q_n)$$

代表仅与广义坐标有关的一项。

如果一个系统的动能的结构如上面式子所示，那么称这个系统是 unnatural。

note

collapse: open title: Note 值得注意的是，很多的unnatural系统与转动的frame相关，此时科里奥利力会充当$T_1$，离心力会充当$T_0$

此时，对于拉格朗日量就有：

$$L=t-V=T_2+T_1-U,U=V-T_0=U(q_1,q_2,\cdots ,q_n)$$

其中 U 代表了修正的动态势能。

进一步，带入哈密顿量的定义，有：

$$\mathcal{H}=\sum _{k=1}^n\frac{\partial L}{\partial {\dot{q}}_k}{\dot{q}}_k-L=2T_2+T_1-(T_2+T_1-U)=T_2+U$$

当 $T_2=T,T_1=T_0=0$ 时，即系统是 natural 时，哈密顿量为：

$$\mathcal{H}=T+V=E$$

也就是导出了能量守恒。

Conservation Laws

在 哈密顿方程 推导过后，我们得到了 2n 个一阶的微分方程，能够更加简明地描述涉及的系统。让我们对哈密顿量进行更细致的一些探讨。

首先考虑这样的情形，即，一个给定的广义坐标 $q_s$，在拉格朗日量中并未出现，那么在哈密顿量中也不可能出现。

comment

collapse: open title: Comment 回顾哈密顿量的定义：$\mathcal{H}={\sum }_{k=1}^n\frac{\partial L}{\partial {\dot{q}}_k}{\dot{q}}_k-L$，在$L$中不出现该坐标，那么$\mathcal{H}$中也不出现

我们称这样的，一个广义坐标在拉格朗日量中不显示的出现，称其为可忽略的 (ignorable)。此外，我们假设非保守力在 $q_s$ 上投影为 0，因此 $Q_{snc}=0$，则根据:

$$\begin{array}{l}{\dot{q}}_k=\frac{\partial \mathcal{H}}{\partial p_k},k=1,2,\dots ,n\\ {\dot{p}}_k=-\frac{\partial \mathcal{H}}{\partial q_k}+Q_{knc},k=1,2,\dots ,n\end{array}$$

有：

$$p_s=constant$$

所以可以说，与该广义坐标对应的广义动量是保守的 (conserved)。

comment

collapse: open title: Comment 可以注意到保守力对应的守恒量：势能V，和这里保守的位移对应的守恒量：动量p之间也存在相似性。

可以认为，上面的广义动量的守恒律是 (角) 动量守恒的推广。

此外，我们考虑在拉格朗日量不显示地依赖于时间 t 的情形，因此使用哈密顿量的定义，对时间进行微分有：

$$\begin{array}{rl}\frac{d\mathcal{H}}{dt}& =\sum _{k=1}^n\left[\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_k}\right){\dot{q}}_k+\frac{\partial L}{\partial {\dot{q}}_k}{\ddot{q}}_k\right]-\sum _{k=1}^n\left(\frac{\partial L}{\partial q_k}{\dot{q}}_k+\frac{\partial L}{\partial {\dot{q}}_k}{\ddot{q}}_k\right)\\ & =\sum _{k=1}^n\left[\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_k}\right)-\frac{\partial L}{\partial q_k}\right]{\dot{q}}_k=\sum _{k=1}^n{Q}_{knc}{\dot{q}}_k\end{array}$$

我们可以认为，右边是非保守力对时间的功率。

这表明了，如果拉格朗日量不显示地依赖于时间，那么哈密顿量和非保守力所做的功有关。

日过非保守力为 0，那么自然的有：$\mathcal{H}=constant$，这体现了另一种守恒律：在拉格朗日量不显示地依赖于时间时，如果所有的非保守力是 0，那么哈密顿量守恒。

进一步的，可以根据之前对系统动能的分析得到：

$$\mathcal{H}=T_2+U=constant$$

因此可以得到关于自然系统的哈密顿量守恒率：

$$\mathcal{H}=T+V=constant$$

这也被称为能量守恒。

一个例子

问题描述

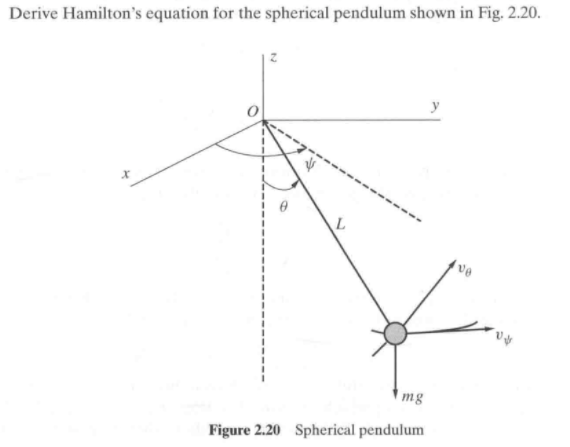
计算求解

对于这样的三维摆问题，求解如下：

可以参考 Mathematica 代码：

ClearAll["Global`*"]
(*Principle and Techniques of Vibrations, P95 Prob*)
v\[Theta] = L D[\[Theta][t], t];
v\[Psi] = L D[\[Psi][t], t] Sin[\[Theta][t]];
T = 1/2 m (v\[Theta]^2 + v\[Psi]^2);
V = m g L (1 - Cos[\[Theta][t]]);
Lag = T - V;
rul1 = Solve[p\[Theta][t] == D[Lag, \[Theta]'[t]], \[Theta]'[t]];
rul2 = Solve[p\[Psi][t] == D[Lag, \[Psi]'[t]], \[Psi]'[t]];
Hil = T + V /. (Flatten[{rul1, rul2}]) // FullSimplify
params = {g -> 9.8, L -> 1, m -> 1};

eqns = {\[Theta]'[t] == D[Hil, p\[Theta][t]] // FullSimplify,
   \[Psi]'[t] == D[Hil, p\[Psi][t]] // FullSimplify,
   p\[Theta]'[t] == -D[Hil, \[Theta][t]] // FullSimplify,
   p\[Psi]'[t] == -D[Hil, \[Psi][t]] // FullSimplify} /. params

(*Solve Problem*)

ic = {\[Theta]'[0] == 0, \[Psi]'[0] == 1, \[Theta][0] == 
   Pi/3, \[Psi][0] == Pi/6}
sol = NDSolve[{eqns, ic} // 
    Flatten, {\[Theta], \[Psi], \[Theta]', \[Psi]'}, {t, 10}];

(*notice that \[Psi] is absent in Lag, which means p\[Psi] is \
constant,system degree of freedom reduce to 1 *)

Plot[Evaluate[\[Theta][t] /. sol], {t, 0, 10}, PlotRange -> All]
Plot[Evaluate[\[Theta]'[t] /. sol], {t, 0, 10}, PlotRange -> All]
ParametricPlot3D[{L Sin[\[Theta][t]] Cos[\[Psi][t]], 
    L Sin[\[Theta][t]] Sin[\[Psi][t]], -L Cos[\[Theta][t]]} /. 
   params /. sol, {t, 0, 10}, AxesLabel -> {x, y, z}]

理论分析

问题

尝试求解下面问题：

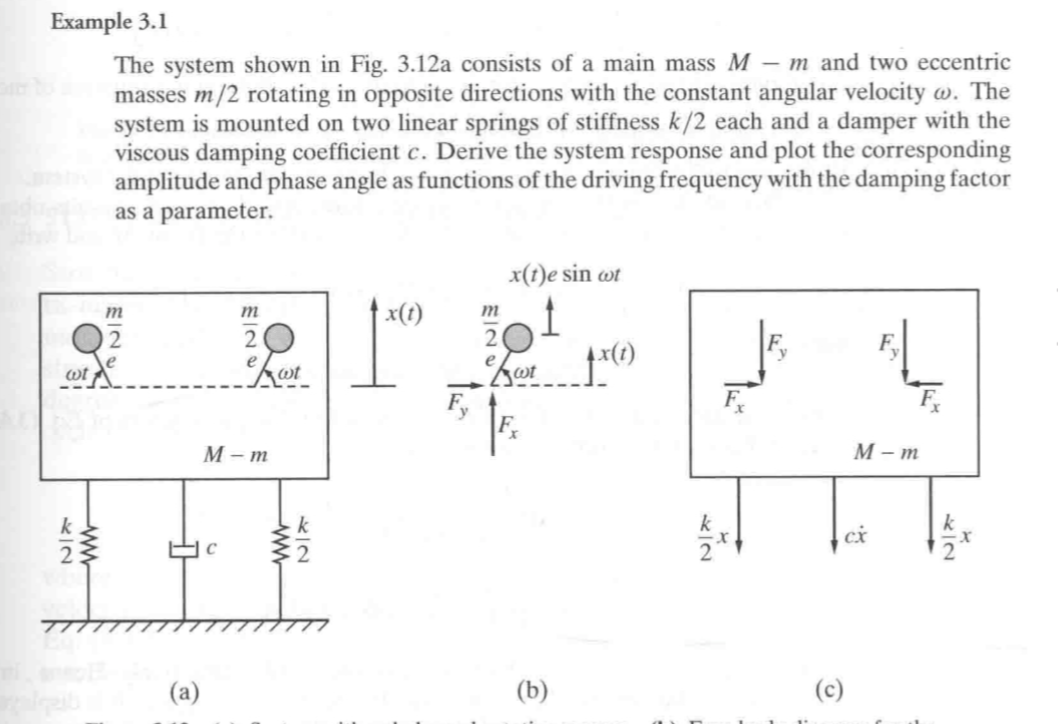
可以发现一来阻尼力作为非保守力，二来内部的旋转激振单元带来常量的动能和显含时间 t 的拉格朗日量，似乎不太好求解??? #todo

参考

• 分析力学笔记（2）虚功原理（其一）基本形式的虚功原理 - 知乎 (zhihu.com)
• @meirovitchPrinciplesTechniquesVibrations