@plestanNewMethodologiesAdaptive2010

plestanNewMethodologiesAdaptive2010

MetaInfo

文献标题

New methodologies for adaptive sliding mode control

Abstract

Contents

问题描述

问题背景

问题难点

在基本无信息的条件下实现自适应估计系统参数的滑模控制

前人工作

本文工作

本文意义

实验方法

问题分析

假定需要控制的非线性系统为：

$$\dot{x}=f\left(x\right)+g\left(x\right)u$$

其中 $x\in R^n$ 是系统的状态变量，f(x) 和 g(x) 是在 x 定义域内 有界的。假定控制的滑模变量为 $\sigma (x,t)$，目的是使得 $\sigma =0$。有

$$\begin{array}{c}\dot{\sigma }=\frac{\partial \sigma }{\partial x}\dot{x}+\frac{\partial \sigma }{\partial t}\\ =\underset{\Psi \left(x,t\right)}{\underbrace{\frac{\partial \sigma }{\partial x}f\left(x\right)+\frac{\partial \sigma }{\partial t}}}+\underset{\Gamma \left(x,t\right)}{\underbrace{\frac{\partial \sigma }{\partial x}g\left(x\right)u}}\end{array}$$

满足：

$$\left|\Psi \right|\le {\Psi }_M,0<{\Gamma }_m\le \Gamma \le {\Gamma }_M$$

这些是我们仅有的条件，下面提出一些本文中的定义：

definition

• 理想滑模面：$S=\left\{\begin{array}{c}x\in \mathcal{X}|\end{array}\sigma \left(x,t\right)=0\right\}$
• 实际滑模面：$S^{\ast }=\left\{\begin{array}{c}x\in \mathcal{X}|\end{array}\left|\sigma \right|<\delta \right\}$

其中理想滑模面物理上不可实现，因此改用实际滑模面替代。

具体算法

problem

提出给定这样一个控制器：

$$\begin{array}{c}u=-K\cdot \mathrm{sign}\left(\sigma \left(x,t\right)\right)\\ \dot{K}=\{\begin{array}{l}\bar{K}\cdot \left|\sigma \left(x,t\right)\right|\cdot \mathrm{sign}\left(\left|\sigma \left(x,t\right)\right|-\epsilon \right)\\ \mu \end{array}\begin{array}{c}\mathrm{if}K>\mu \\ \mathrm{if}K>\mu \end{array}\end{array}$$

其中$K\left(0\right)>0,\bar{K}>0,\epsilon >0,\mu >0$且$\mu$很小。那么，可以证明，这样的控制器满足上面的要求

^eqn-control-law

首先，不失一般性，可以假设对任意时刻，$K(t)>\mu$。这很明显可以从我们 K 的取值看出。

lemma

在上面提出的非线性系统下，提出的增益K存在上界，即：

$$K\left(t\right)\le K^{\ast }\forall t>0$$

证明参考 APL1

进一步，给出这样的结论：

lemma

对上面的非线性系统和控制方法，存在有限的时间$t_F>0$使得实际滑模面在所有$t>t_F$的时候成立，即：

$$\begin{array}{c}\left|\sigma \left(x,t\right)\right|<\delta \forall t⩾t_F\\ \delta =\sqrt{{\epsilon }^2+\frac{{\Psi }_M^2}{\bar{K}{\Gamma }_m}}\end{array}$$

考虑李雅普诺夫函数，有：

$$V=\frac{1}{2}{\sigma }^2+\frac{1}{2\gamma }{\left(K-K^{\ast }\right)}^2$$

从而微分有：

$$\begin{array}{c}\dot{V}=\sigma \left(\Psi -\Gamma K\mathrm{sign}\left(\sigma \right)\right)+\frac{1}{\gamma }\left(K-K^{\ast }\right)\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)\\ \le {\Psi }_M\left|\sigma \right|-{\Gamma }_{m}K\left|\sigma \right|+\frac{1}{\gamma }\left(K-K^{\ast }\right)\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)\\ ={\Psi }_M\left|\sigma \right|-{\Gamma }_{m}K\left|\sigma \right|+\underset{\text{构造项}}{\underbrace{{\Gamma }_m{K}^{\ast }\left|\sigma \right|-{\Gamma }_m{K}^{\ast }\left|\sigma \right|}}+\frac{1}{\gamma }\left(K-K^{\ast }\right)\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)\\ =\left({\Psi }_M-{\Gamma }_m{K}^{\ast }\right)\left|\sigma \right|+\left(K-K^{\ast }\right)\left(-{\Gamma }_m\left|\sigma \right|+\frac{1}{\gamma }\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)\right)\end{array}$$

进一步添加构造项 ${\beta }_K>0$ 有：

$$\begin{array}{c}\dot{V}=\left({\Psi }_M-{\Gamma }_m{K}^{\ast }\right)\left|\sigma \right|+\left(K-K^{\ast }\right)\left(-{\Gamma }_m\left|\sigma \right|+\frac{1}{\gamma }\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)\right)\\ +{\beta }_K\left|K-K^{\ast }\right|-{\beta }_K\left|K-K^{\ast }\right|\end{array}$$

注意到根据上面的 Lemma1 有 $K\left(t\right)-K^{\ast }<0\forall t>0$，从而

$$\begin{array}{c}\dot{V}=-\underset{{\beta }_{\sigma }>0}{\underbrace{\left(-{\Psi }_M+{\Gamma }_m{K}^{\ast }\right)}}\left|\sigma \right|-{\beta }_K\left|K-K^{\ast }\right|\\ -\underset{\xi }{\underbrace{\left|\underset{<0}{\underbrace{K-K^{\ast }}}\right|\left(-{\Gamma }_m\left|\sigma \right|+\frac{1}{\gamma }\bar{K}\left|\sigma \right|\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)-{\beta }_K\right)}}\end{array}$$

这意味着：

$$\begin{array}{c}\dot{V}=-{\beta }_{\sigma }\left|\sigma \right|-{\beta }_K\left|K-K^{\ast }\right|-\xi \\ =-{\beta }_{\sigma }\sqrt{2}\frac{|\sigma |}{\sqrt{2}}-{\beta }_K\sqrt{2\gamma }\frac{|K-K^{\ast }|}{\sqrt{2\gamma }}-\xi \\ \le -\min \left\{{\beta }_{\sigma }\sqrt{2},{\beta }_K\sqrt{2\gamma }\right\}\left(\frac{|\sigma |}{\sqrt{2}}+\frac{|K-K^{\ast }|}{\sqrt{2\gamma }}\right)-\xi \\ \le -\beta V^{1/2}-\xi \beta =\min \left\{{\beta }_{\sigma }\sqrt{2},{\beta }_K\sqrt{2\gamma }\right\}\end{array}$$

现在分析 $\xi$ 的情况。

• Case1: $\left|\sigma \right|>\epsilon$$\left|\sigma \right|>\epsilon$，此时有

$$\begin{array}{c}\xi =-{\Gamma }_m\left|\sigma \right|+\frac{1}{\gamma }\bar{K}\left|\sigma \right|\underset{=1}{\underbrace{\mathrm{sign}\left(\left|\sigma \right|-\epsilon \right)}}-{\beta }_K>0\\ ⟺\gamma <\frac{\bar{K}|\sigma |}{{\Gamma }_m|\sigma |+{\beta }_K}\end{array}$$

注意到右边函数是增函数，因此取：

$$\gamma <\frac{\bar{K}\epsilon }{{\Gamma }_m\epsilon +{\beta }_K}$$

此时有：

$$\dot{V}\le -\beta V^{1/2}-\xi \le -\beta V^{1/2}$$

根据李雅普诺夫收敛的性质，这表明在任何 $\left|\sigma \right|>\epsilon$ 的条件下，控制对象在有限时间内收敛

• Case2: $\left|\sigma \right|<\epsilon$ 此时 $\xi$ 可能为负这意味着李雅普诺夫的思路不能完全成功，但可以注意到，一旦 $\left|\sigma \right|>\epsilon$，立马问题就解决了。因此我们需要考虑的就是分析状态切换需要的时间代价和精度问题。

记 ${\sigma }_0=\sigma \left(0\right)={\epsilon }^{+}$，$K_0=\mathcal{K}\left(0\right)=K\left(0\right)$。不失一般性，可以假设 ${\sigma }_0>0$，否则其会一直增长。考虑 最坏情形，即：

$$\begin{array}{c}\dot{\sigma }={\Psi }_M-K{\Gamma }_m\\ \dot{K}=\bar{K}\left|\sigma \right|\end{array}$$

这里的最坏情形意思是放任 $\sigma$ 增大，此时偏离滑模面的误差最大的情况。

根据上面的方程可以解得：

$$\begin{array}{rl}\sigma (t)=& {\sigma }_0\cos \left(\sqrt{\bar{K}{\Gamma }_m}t\right)+\frac{{\Psi }_M-K_0\cdot {\Gamma }_m}{\sqrt{\bar{K}{\Gamma }_m}}\cdot \sin \left(\sqrt{\bar{K}{\Gamma }_{m}t}\right)\\ K(t)=& {\sigma }_0\sqrt{\frac{\bar{K}}{{\Gamma }_m}}\sin \left(\sqrt{\bar{K}{\Gamma }_{m}t}\right)+\left(K_0-\frac{{\Psi }_M}{{\Gamma }_m}\right)\\ & \times \cos \left(\sqrt{\bar{K}{\Gamma }_{m}t}\right)+\frac{{\Psi }_M}{{\Gamma }_m}\end{array}$$

从而得到：

$$\begin{array}{l}\sigma (t)=\sqrt{{\sigma }_0^2+\frac{{\left({\Psi }_M-K_0\cdot {\Gamma }_m\right)}^2}{\bar{K}{\Gamma }_m}}\sin \left(\sqrt{\bar{K}{\Gamma }_m}t+{\Theta }_{\sigma }\right)\\ K(t)=\sqrt{{\sigma }_0^2\frac{\bar{K}}{{\Gamma }_m}+{\left(K_0-\frac{{\Psi }_M}{{\Gamma }_m}\right)}^2}\sin \left(\sqrt{\bar{K}{\Gamma }_m}t+{\Theta }_K\right)+\frac{{\Psi }_M}{{\Gamma }_m}\end{array}$$

因此可以发现，在 ${\sigma }_0={\epsilon }^{+}\to \epsilon$ 时，最大的误差满足

$$\begin{array}{c}{\sigma }_M=\sqrt{{\sigma }_0^2+\frac{{\left({\Psi }_M-K_0\cdot {\Gamma }_m\right)}^2}{\bar{K}{\Gamma }_m}}\\ \le \sqrt{{\epsilon }^2+\frac{{\Psi }_M^2}{\bar{K}{\Gamma }_m}}\end{array}$$

这意味着 $\sigma$ 可以在有限时间内收敛到 case1 中的情况内，满足之前定义的真实滑模面

总的来说，论文基本到这里论证就结束了，后面还有一些关于参数优化的结论，这里就不展开了。

辅助证明

APL1

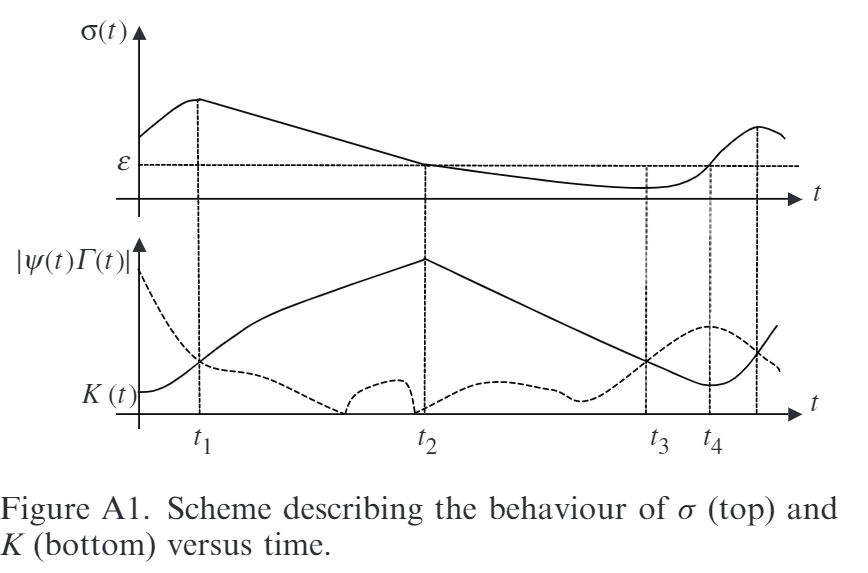
参考上面这张例图。图上半部分是滑模变量随着时间变化的图，下半部分是 K 随着时间变化的图。

假定一开始 $\left|\sigma \left(x,t\right)\right|>\epsilon$，则根据提出的控制器规则，^eqn-control-law， K 会一直增加，直到一个 t1 时刻使得 u 足够大，此时滑模变量 $\sigma$ 开始减小。在此之后，K 会继续增大，直到 $\sigma$ 再次碰到 $\epsilon$，此时 K 在 t2 时刻达到最大。继续这个进程，K 开始减小，直到 t3 时刻，K 太小以至于无法抵消外界扰动 (也就是使得 $\sigma$ 斜率再次为 0)。再进一步此时 K 增大 (这里意思是 K 不会太小，基本上会周期扰动)，达到时刻 t4,回到一开始的起点。

note

论文中感觉不太对，不是所有点都满足$\left|\dot{\sigma }\right|=0$

在这几段时间中，根据我们的分析，所有的 K 值是在 t1,t2,t3,t4 这四个点之中的，有：

$$K\le \frac{\left|\dot{\sigma }\right|+{\Psi }_M}{{\Gamma }_m}$$

其中在 t1,t3 点 $\left|\dot{\sigma }\right|$ 为 0。由于这是光滑的现实系统，因此 $\left|\dot{\sigma }\right|$ 是有界的，从而 K 存在上界 $K^{\ast \ast }$，进而存在一个有限的 $K^{\ast }$ 使得其为上界。

优点缺点

优点

缺点

个人评价

我个人觉得论文论证有点不太严谨，比如 APL1 部分或许就存在一些问题。

此外，论文里面的 switch function 全部使用的 sign 这种不连续函数，这会导致剧烈的 K 值抖动，进而影响控制量 u 的相位。这一现象在达到了真实滑模面后更加明显，小范围的相位变化很常见，这一问题可以通过采用光滑的切换函数 (eg. tanh) 实现。