@edwardsAdaptiveContinuousHigher2016

edwardsAdaptiveContinuousHigher2016

MetaInfo

文献标题

Adaptive continuous higher order sliding mode control

Abstract

This paper is concerned with the development of an adaptation structure which can be applied to conventional, super-twisting and higher-order sliding mode schemes. The objective is to alter the modulation gains associated with these schemes in such a way that they are as small as possible to mitigate chattering effects, but large enough to ensure that sliding can be maintained in the presence of bounded and derivative bounded uncertainties. In all the proposed schemes, the equivalent control is used to drive the adaptive mechanism. The approach is based on a novel dual layer nested adaptive methodology which is quite different to the existing schemes proposed in the sliding mode literature. The new adaptive schemes do not require knowledge of the minimum and maximum allowed values of the adaptive gain, and in their most general form, do not require information about the bound on the disturbances and their derivatives.

Contents

问题描述

问题背景

1. The insensitivity and finite time convergence properties en-joyed by sliding mode controllers make them a useful approachfor systems with significant uncertainties
   1. these robust-ness properties come at a cost, usually termed ‘chattering’, result-ing from high frequency switching of the control signal
2. Higher-order-sliding-modes offers significant chattering mitigation through increasing the input-output relative degree, providing continous signal
   1. contains structure pre-calculated by some bounds on the uncertainties (or derivatives of uncertainties )
   2. conservative upper bound are used to gurantee that sliding will take place
      1. conservation exacerbates chattering associated with the implementation
3. Motivate #ASMC whereby the gains in controller adapt to a level where they are as small as possible and yet gurantee sliding is maintained

前人工作

前人缺陷

本文工作

1. propose new equivalent control-based adaptive schemes for conventional , super-twisting and continous higher order sliding mode control algorithms
2. the scheme allows magnitude and rate of change of the controller parameters to adapt whilst guranteeing a sliding motion

本文意义

实验方法

SISO Formulation

Problem Reform

consider a fitst-order sliding mode equation representing the dynamics of the switching variable:

$$\dot{\sigma }\left(t\right)=a\left(t\right)+u\left(t\right)$$

^eqn-siso-formualtion

assume that $|a(t)|<a_0$ and $|\dot{a}(t)|<a_1$, consider the control law:

$$u\left(t\right)=-\left(k\left(t\right)+\eta \right)\mathrm{sign}\left(\sigma \left(t\right)\right)$$

^eqn-siso-control-law

where $\eta$ is a small positive design constant and $k(t)$ is a varing scalar term

Note that when $k(t)>|a(t)|$, the $\eta$ -reachability condition $\sigma \dot{\sigma }<-\eta \left|\sigma \right|$ is satisfied

note

should be $k(t)+\eta >|a(t)|$??

Based on previous paper, during sliding motion ($\sigma =0$), the so called equivalent contol $u_{eq}(t)$ should maintain $\dot{\sigma }=0$, so that $u_{eq}(t)=-a(t)$. Because a is unknown, we can obtain a close approximation by taking low-pass filter of the switch signal u(t):

$${\dot{\bar{u}}}_{eq}=\frac{1}{\tau }\left(-\left(k\left(t\right)+\eta \right)\mathrm{sign}\left(\sigma \left(t\right)\right)-{\bar{u}}_{eq}\left(t\right)\right)$$

Based on previous paper, when $\tau >0$ is small enough, $\left|{\bar{u}}_{eq}\left(t\right)-u_{eq}\left(t\right)\right|$ can be small enough.

Assumption

exists a scalar $1>{ϵ}_1>0$ and ${ϵ}_0>0$ such that:

$$\left|\left|{\bar{u}}_{eq}\left(t\right)\right|-\left|u_{eq}\left(t\right)\right|\right|<{ϵ}_1\left|u_{eq}\left(t\right)\right|+{ϵ}_0$$

holds for all time after a finite time $t_{e}q$, to allow for the (fast) dissipation of the effects of the initial condition of the filter

^assum-1

Introduce a safety margin, rewrite the objective:

$$k\left(t\right)>\frac{1}{\alpha }\left|{\bar{u}}_{eq}\left(t\right)\right|+ϵ$$

where $0<\alpha <1$ and $ϵ>0$ are designed scalar(depending on ${ϵ}_0$ and ${ϵ}_1$) chosen to ensure the estimate ${\bar{u}}_{eq}(t)$ satisfies:

$$\frac{1}{\alpha }\left|{\bar{u}}_{eq}\left(t\right)\right|+\frac{ϵ}{2}>\left|u_{eq}\left(t\right)\right|$$

Now define an error variable:

$$\delta \left(t\right)=k\left(t\right)-\left(\frac{1}{\alpha }\left|{\bar{u}}_{eq}\left(t\right)\right|+ϵ\right)$$

^eqn-siso-error

Notice that when $\delta =0$ the $k(t)>|u_{eq}(t)|>|a(t)|$, so the target is to forcing $\delta \left(t\right)\to 0$, so that the $k(t)+\eta >|a(t)|$ can be guranted.

note

1. this methodology is basically to broaded the sliding manifold
2. the trick here is to introduce a small constant to seperate target and approximation

corollary

Till now, the problem is reformed as a tracking problem, target is to gurantee error variable $\delta \to 0$

New Methodology

The k(t) in ^eqn-siso-control-law can will be formed below:

$$\dot{k}\left(t\right)=-\rho \left(t\right)\mathrm{sign}\left(\delta \left(t\right)\right)$$

^eqn-siso-k-adapt

In this paper, author give a form of $\rho$ as :

$$\rho (t)=r_0+r(t)$$

Based on different prior knowledge of uncertainties , different adaption law is proposed

When Bound a1 is Known

Assumption

In this subsection, $a_0$ is assumed to be unknown but bounded, but $a_1$ is available, i.e. the worst case rate of change of the disturbances

define :

$$e\left(t\right)=\frac{q{a}_1}{\alpha }-r\left(t\right)$$

where user-define scalar $q>1$ is a safety margin chosed to ensure:

$$\left|\frac{\mathrm{d}}{\mathrm{d}t}\left({\bar{u}}_{eq}\left(t\right)\right)\right|<q{a}_1$$

^eqn-q-design

Give the adaption scheme :

definition

$$\dot{r}\left(t\right)=\gamma \left|\delta \left(t\right)\right|+r_0\sqrt{\gamma }\mathrm{sign}\left(e\left(t\right)\right)$$

where $\gamma >0$ is a design scalar

^eqn-siso-a1-adapt

By analysing the Lyaponov function:

$$V=\frac{1}{2}{\delta }^2+\frac{1}{2\gamma }{e}^2$$

and can ensure:

$$\dot{V}⩽-r_0\sqrt{2V}$$

so $\delta (t)$ and $e(t)$ converge to 0 in finite time, and makes k satisfy condition

When Bound a1 and a0 Are Both Unknown

since $a_1$ is unknown, update the adaptive scheme as below:

$$\dot{r}\left(t\right)=\{\begin{array}{l}\gamma \left|\delta \left(t\right)\right|\\ 0\end{array}\begin{array}{c}\mathrm{if}\left|\delta \left(t\right)\right|>{\delta }_0\\ \mathrm{otherwise}\end{array}$$

where ${\delta }_0>0$ is a designed scalar

theorem

Consider above dual-adaptive sliding mode control law, and the uncertainties $a(t)$ satisfy: $|a(t)|<a_0$ and $|\dot{a}(t)|<a_1$, where $a_0$ and $a_1$ are finite but unknown.

If choose $ϵ$ to satisfy :

$$\frac{1}{4}{ϵ}^2>{\delta }_0+\frac{1}{\gamma }{\left(\frac{q{a}_1}{\alpha }\right)}^2$$

for any given ${\delta }_0$ and $a_1$, then the control law forces $|\delta (t)|<ϵ/2$ in finite time and consequently ensures a sliding motion can be sustained.

^themrem-siso-a0-a1

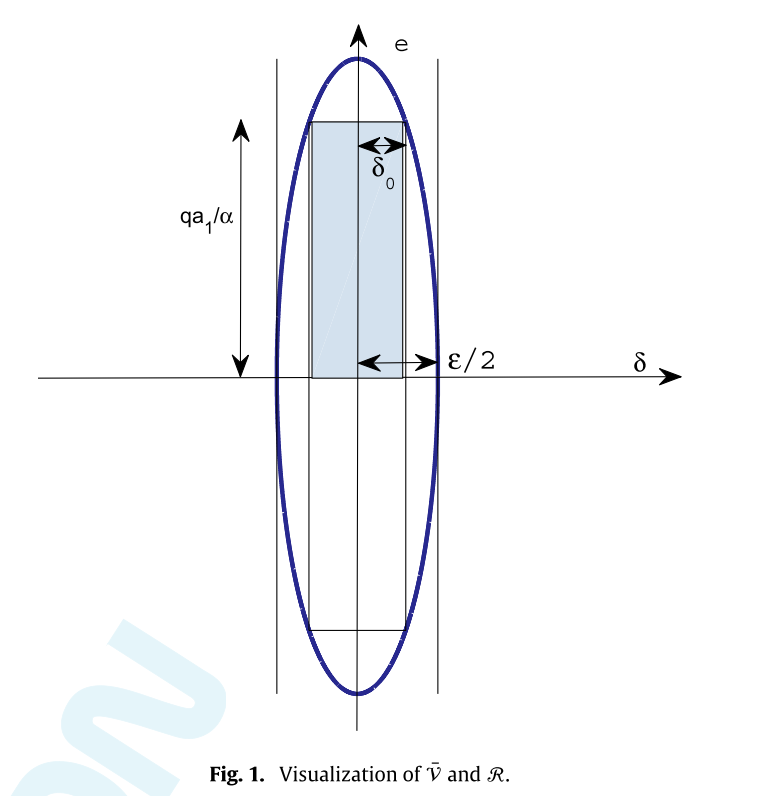
remark

1. The scalar ${\delta }_0$ needs to be larger than noise or computational errors
2. The user defined parameters $ϵ$, $\alpha$ are the safety factors whilst $q$ reflects the accuracy associated with the estimation of the equivalent control
3. though $a_1$ is unknown, by selecting the adaptive gain $\gamma$ sufficiently large (to dominate $a_1$), for any value of ${\delta }_0$ , $q$ and $a_1$ there always exists an $ϵ$ to ensure ^themrem-siso-a0-a1 is satisfied
   1. the order of magnitude of $a_1$ should be known
   2. or can be choosed by simulation

note

看看人家怎么写解释的

Example

优点缺点

优点

• based on a dual-layer adaptive approach, do not rely on uncertainties
• adaptive idea can be deploy to conventional , super-twisting , higher-order control structure

缺点

1. not actually model-free
2. the accuracy of second-order method is low, and the direct method has chattering

个人评价

1. Normal
2. the idea of deploy adaptive law to other control scheme is great
3. some tricks applied in demonstration is great

复现实验

我用 simulink 尝试复现其中的 Example 1，即最简单的 SISO 的模型，模型如下：

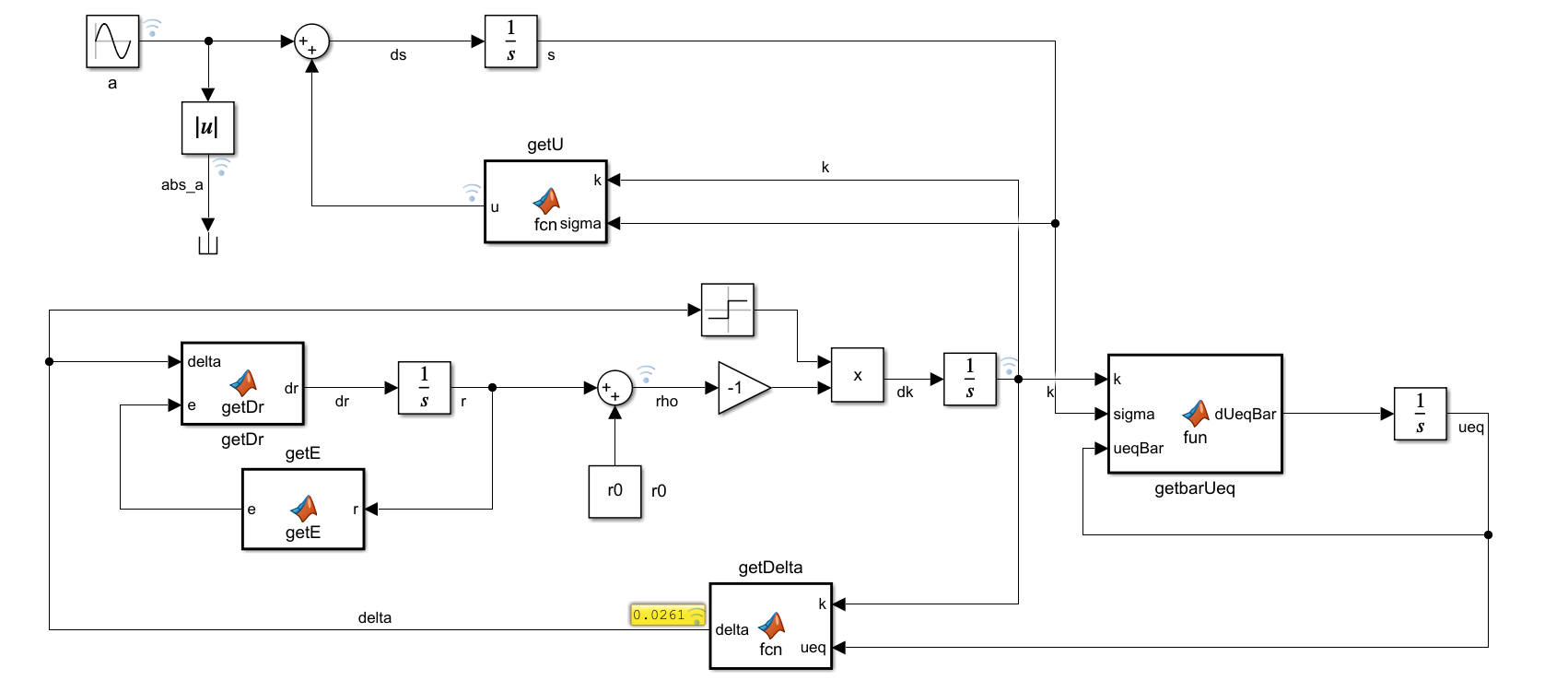
环境为: Matlab 2022a

asmc_edward_init

asmc_edward

作者给出了相关的参数，除了 $q$ 这个自定义的参数。

不得不吐槽，这个方法参数怎么这么多

由于没有给定 q，论文中给了一个 q 的设计准则：

^eqn-q-design

这里的 $a_1$ 取 1，那么需要 q 大于 ${\bar{u}}_{eq}$ 的微分，即大概是 a 的微分，那么 q>1 就可以了

note

不得不吐槽，这作者设计的算法仿真真的感觉有问题，太容易受扰动了，至少我用adaptive的结果太慢了，只能用定点的0.001步长仿真

note

还有一点可以吐槽，这个作者画的图，比如fig4，纵坐标轴都到3去了，误差就算在0.2也看不出来

仿真 1：q=1

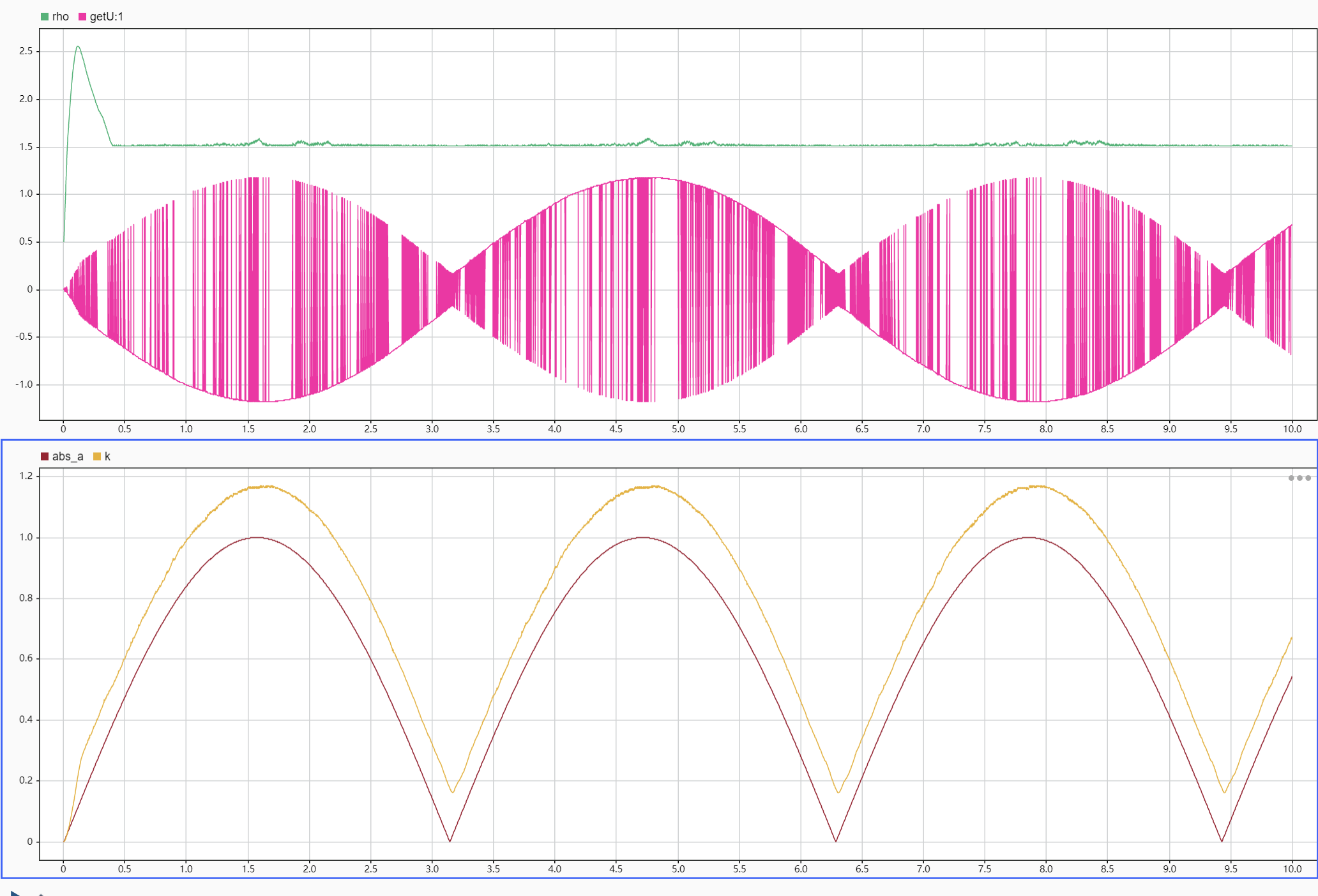
note

取0.0001的步长仿真3s结果为：

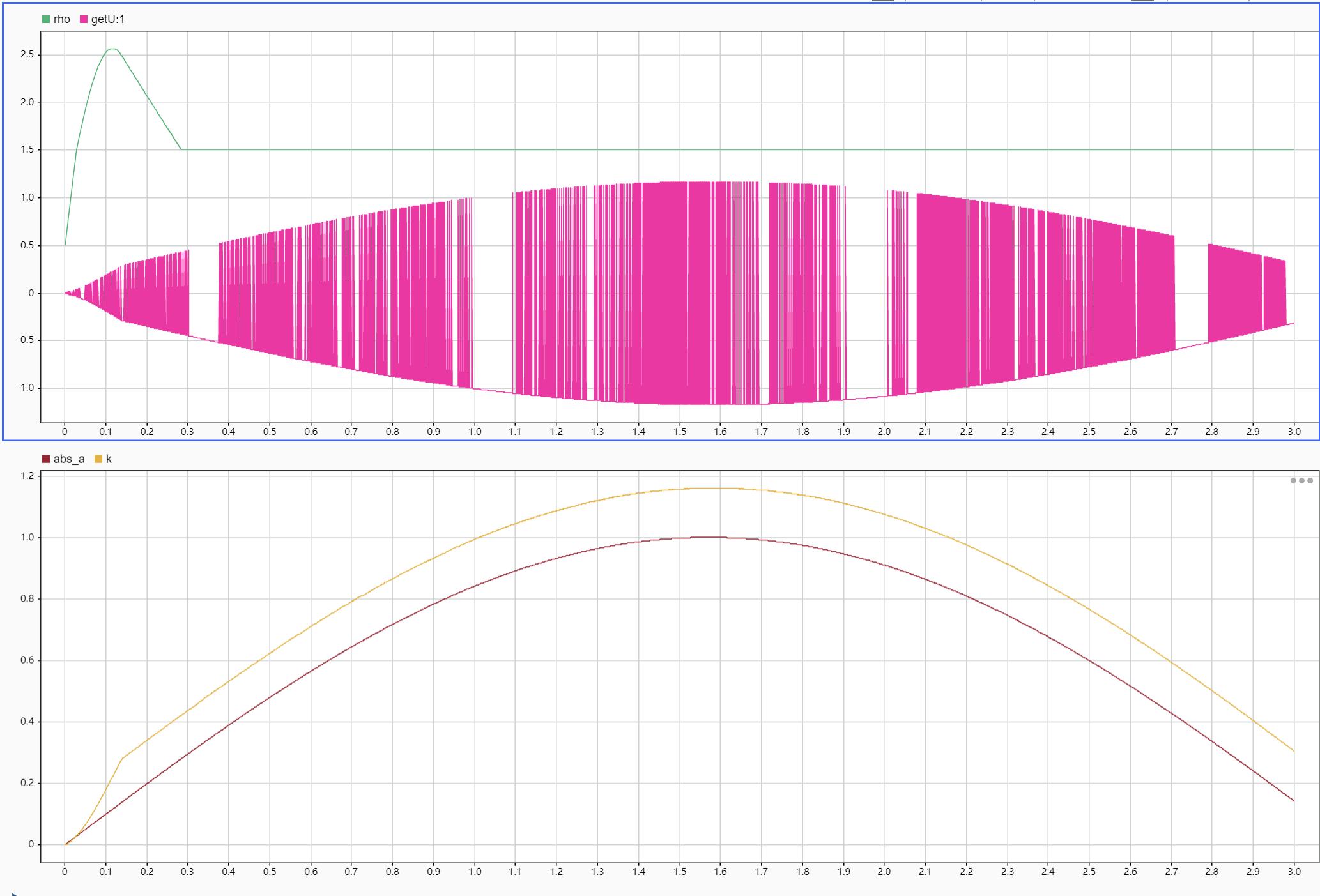
所以不是我仿真不行，是这个算法真的不对

仿真 2：q=1.5

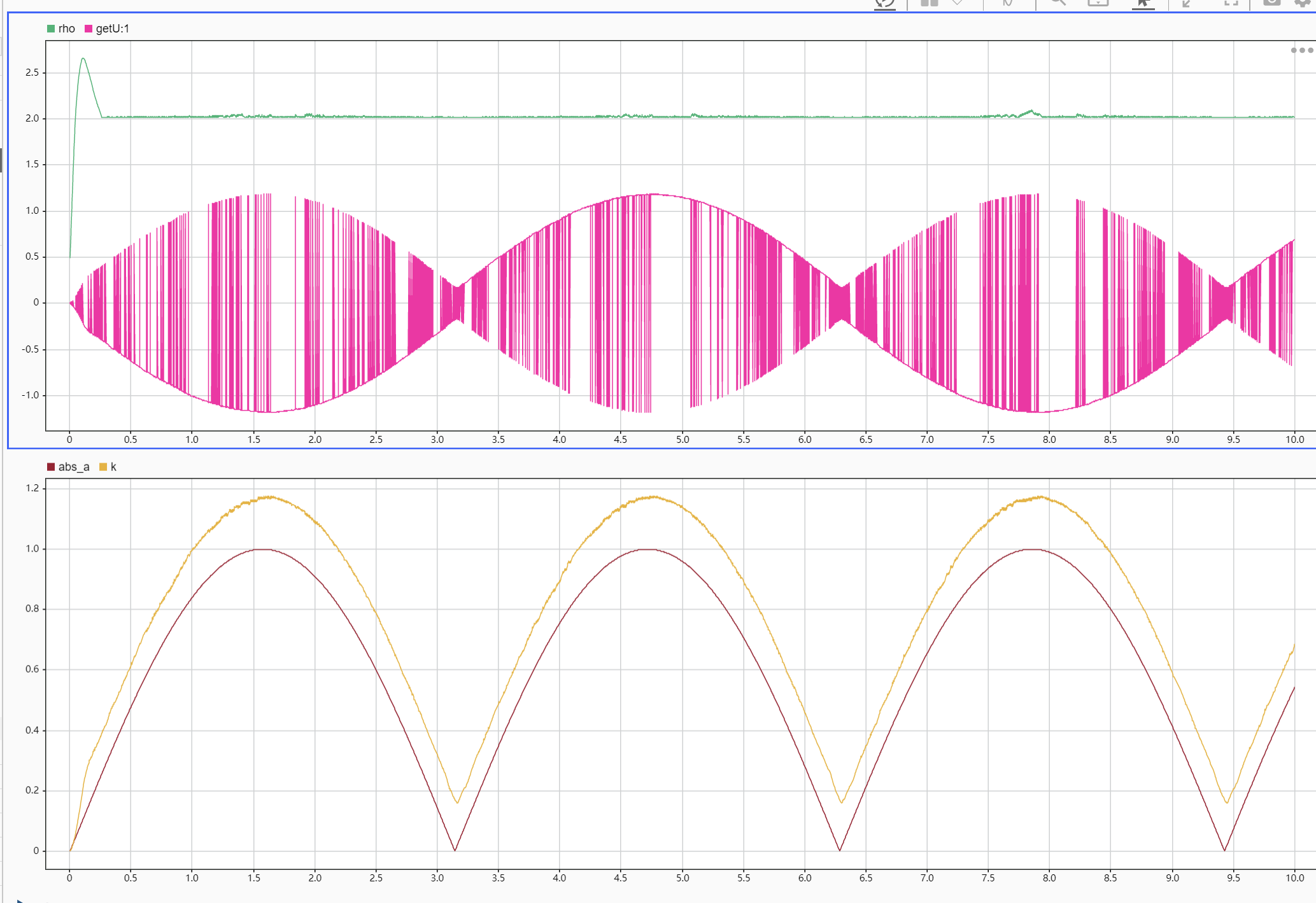
可以看到形式上和作者结果一样，但是精度实在太差

仿真 3：q=5

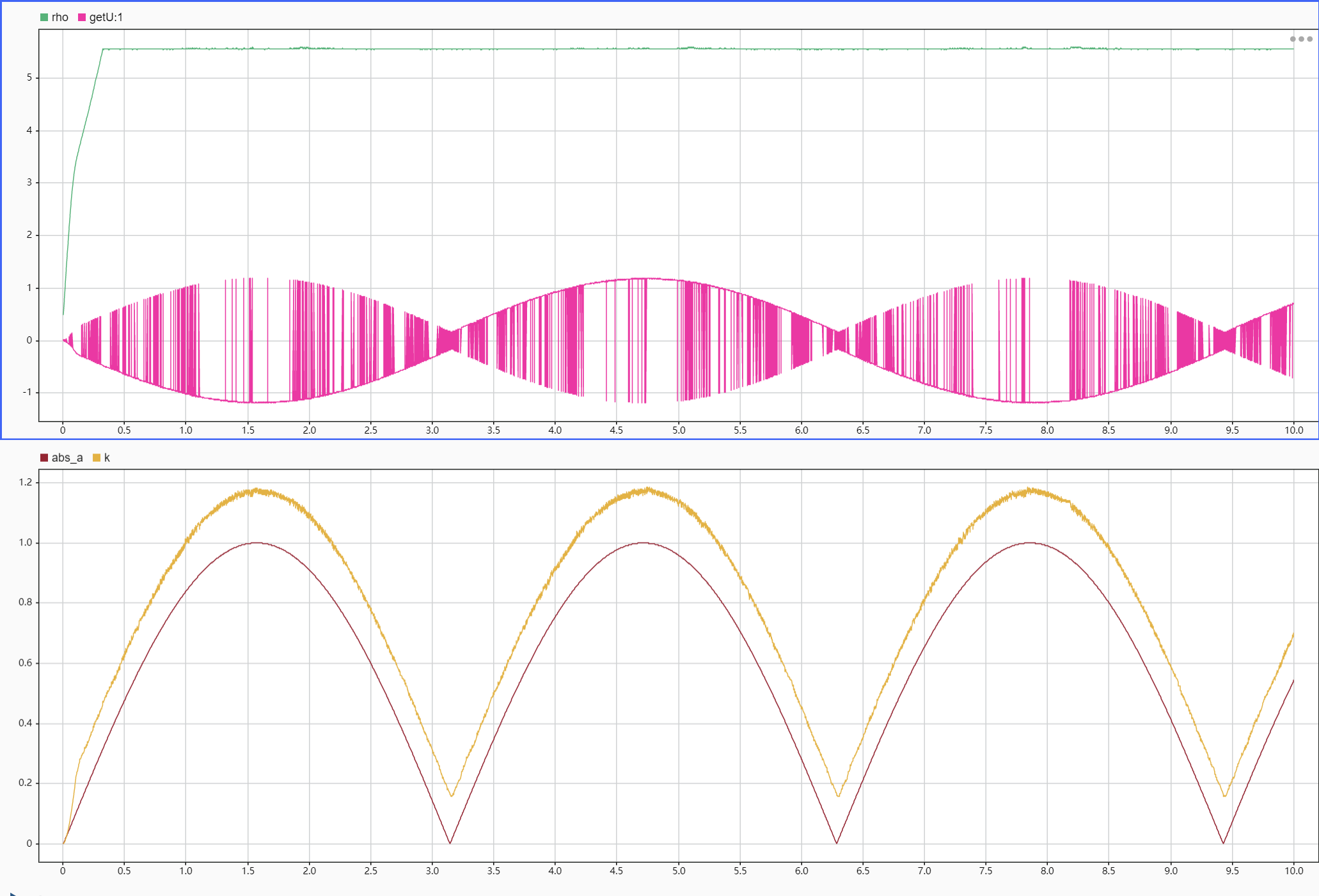
真的不对