摩擦力建模

定义

对摩擦力的模型进行介绍，并介绍了解到的辨识方法，主要分为：

• 平动摩擦
• 转动摩擦

方案

平动摩擦

转动摩擦

动力学模型

经典模型

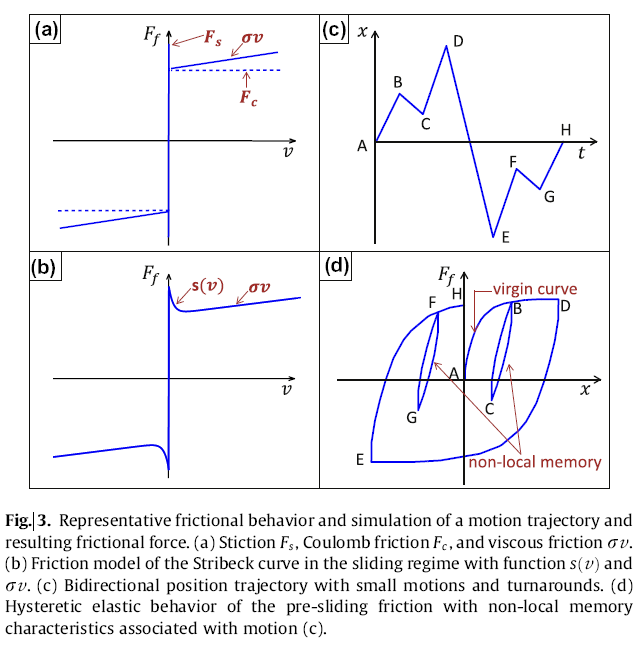
经典的平动的摩擦模型是 $F=\mu N$，这是一种库伦摩擦力的体现。当其中引入了 static friction 和一个线性的 viscous drag term 后，其摩擦力图景如图 ^img-fig3 的 (a) 所示。如果增加了滑动状态下的连续速度依赖性，就得到了 Stribeck 提出的模型，如图 (b) 所示，形式为：

$$F\left(v\right)=s\left(v\right)+\sigma v=\text{sgn}\left(v\right)\left(F_c+\left(F_s-F_c\right)\exp \left({\left|\frac{v}{V_s}\right|}^{\delta }\right)\right)+\sigma v$$

其中包含了 vsicous friction，且：

• $F_c$ 代表 Coulomb friction
• $F_s$ 代表 Static friction
• $V_s$ 代表 stribeck velocity
• $\delta$ 代表 shape factor
• $\sigma$ 代表 viscous coefficient

这一模型经常被称为 static 的因为该模型的参数是可以直接通过常值速度下的试验测量得到的。这一模型有一个大的缺点在于其 0 点不连续性，从而无法解释：

• friction lag
• rate-dependent breakaway force
• hysteresis with non-local memory

^img-fig3

扩展模型——GMS

为了解决上面提出的问题，提出了 GMS 模型

$$\begin{array}{l}\frac{\mathrm{d}{F}_i}{\mathrm{d}t}=k_{i}v,\mathrm{if}stick\\ \frac{\mathrm{d}{F}_i}{\mathrm{d}t}=\text{sgn}\left(v\right)C\left({\alpha }_i-\frac{F_i}{s\left(v\right)}\right),\mathrm{if}slip\\ F_f={\sum }_{i=1}^N{F}_i\left(t\right)+\sigma v\left(t\right)\end{array}$$

其中 C 是一个 attraction factor 决定了 slipping dynamics 跟随速度曲线的变化速率

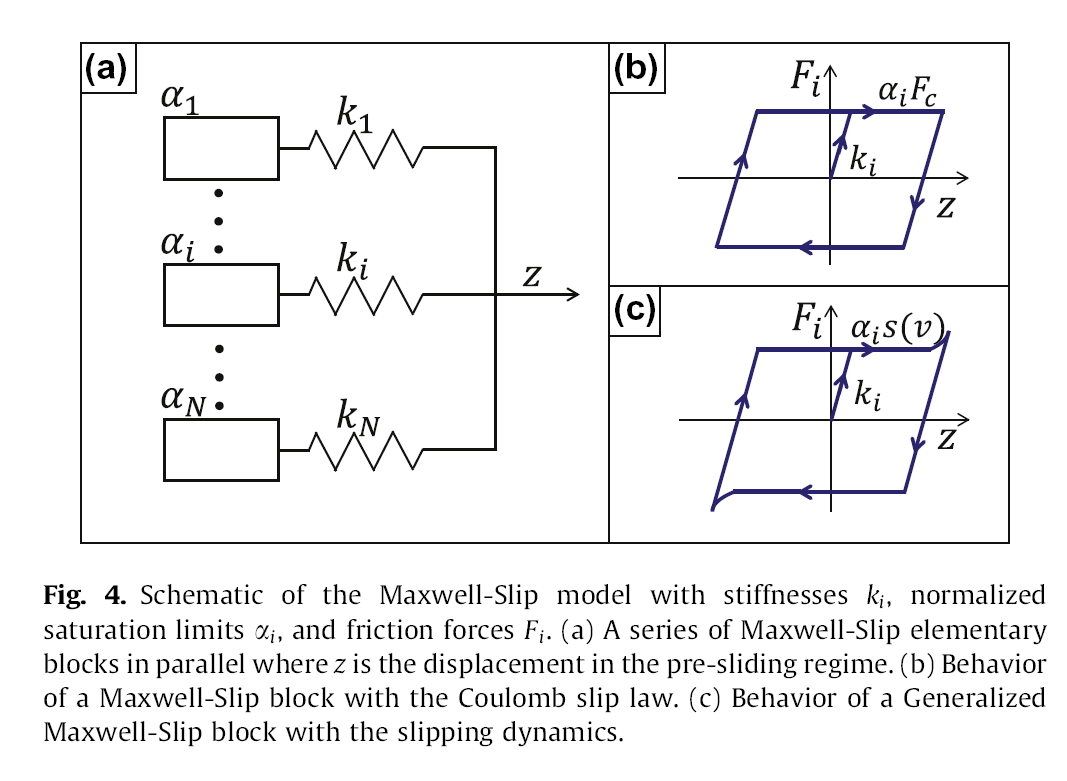
其参数辨识和具体细节可以参考：

@yoonFrictionModelingIdentification2014

经典模型——形式 2

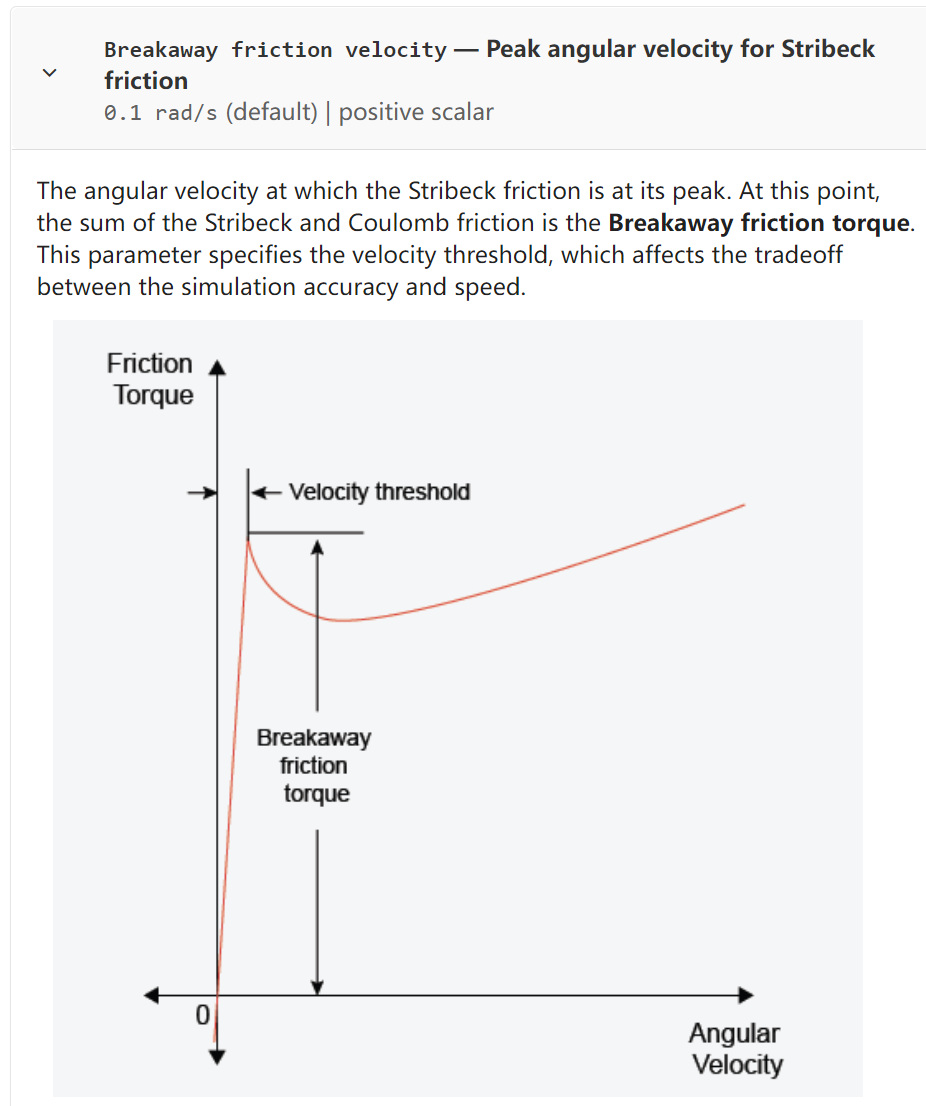
转动摩擦的动力学模型被写为下面的形式：

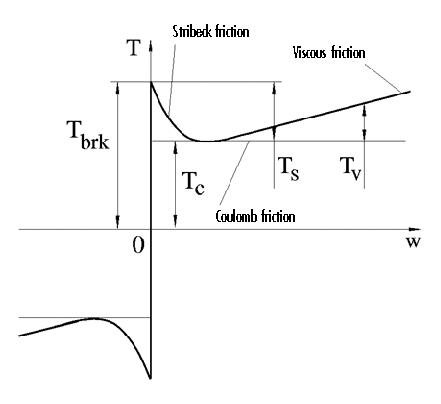
其中可以分为 3 个部分：

• Stribeck friction $T_S$ ：在低速情况下的反向曲线
• Coulomb friction $T_C$ ：在任何速度下的恒定力矩
• Viscous friction $T_V$ ：和相对速度成正比的力矩

完整的摩擦力力矩表达式为：

$$\begin{array}{rl}T& =\sqrt{2e}\left(T_{brk}-T_C\right)\cdot \exp \left(-{\left(\frac{\omega }{{\omega }_{St}}\right)}^2\right)\cdot \frac{\omega }{{\omega }_{St}}+T_C\cdot \tanh \left(\frac{\omega }{{\omega }_{Coul}}\right)+f\omega \\ {\omega }_{St}& ={\omega }_{brk}\sqrt{2}\\ w_{Coul}& ={\omega }_{brk}/10\\ \omega & ={\omega }_R-{\omega }_C\end{array}$$

其中：

• $T$ 是摩擦力矩
• $T_C$ 是 Coluomb 摩擦力矩
• $T_{brk}$ 是启动的 breakaway 力矩
• $w_{brk}$ 是 breakaway friction velocity
  • 
• $w_{St}$ 是 Stribeck velocity threshold
• $w_{Coul}$ 是 Coulomb velocity threshold
• $w_R,w_C$ 是相对的两物体 R 和 C 的角速度
• $w$ 是相对速度
• $f$ 是 viscous friction 系数

其相关的数值模拟可以参考：

• Mechanical Rotational System with Stick-Slip Motion - MATLAB & Simulink - MathWorks 中国

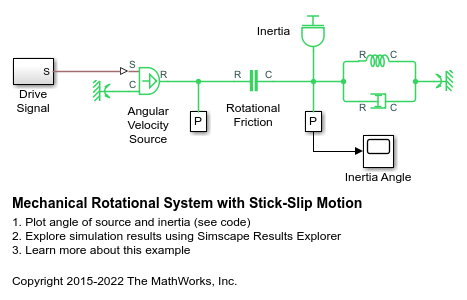
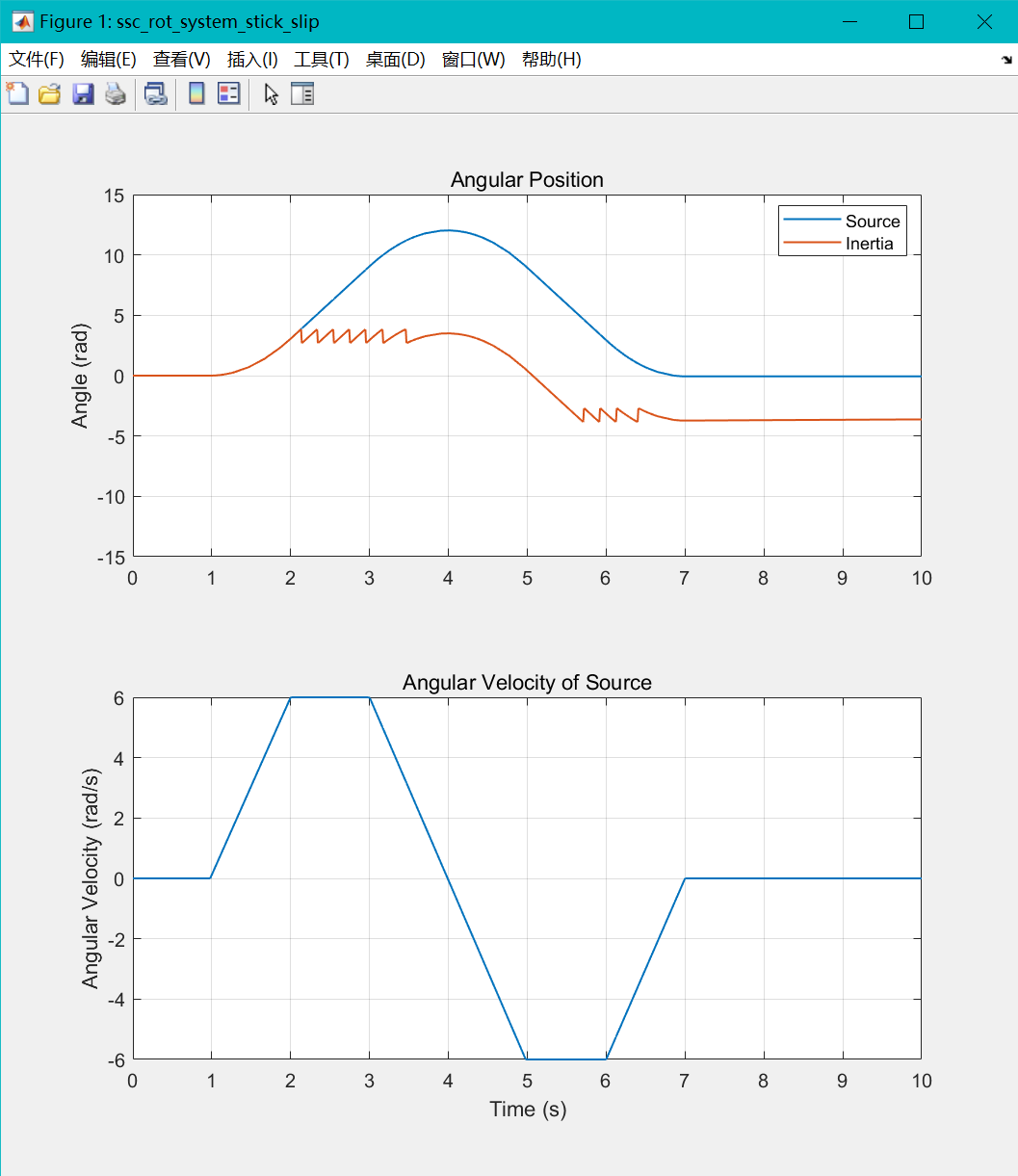
摩擦辨识测试

根据提供的摩擦力式子，构造摩擦力如下：

P.Tbrk = 50;
P.Tc = 20;
P.wbrk = 0.2;
P. f = 0.1;

w = -20:1e-3:20;
T = arrayfun(@(x) fm1(x, P), w);
plot(w, T)

其中函数为：

function T = fm1(w, P)
Tbrk = P.Tbrk;
Tc = P.Tc;
wbrk = P.wbrk;
f = P.f;

wst = wbrk/sqrt(2);
wcoul = wbrk/10;

T = sqrt(2*exp(1))*(Tbrk-Tc)*exp(-(w/wst)^2)*w/wst + Tc*tanh(w/wcoul) + f*w;

end

用于拟合的函数为：

sqrt(2*exp(1))*(Tbrk-Tc)*exp(-(w/(wbrk/sqrt(2)))^2)*w/(wbrk/sqrt(2))+ Tc*tanh(w/(wbrk/10)) + f*w;

做出的摩擦力图为：

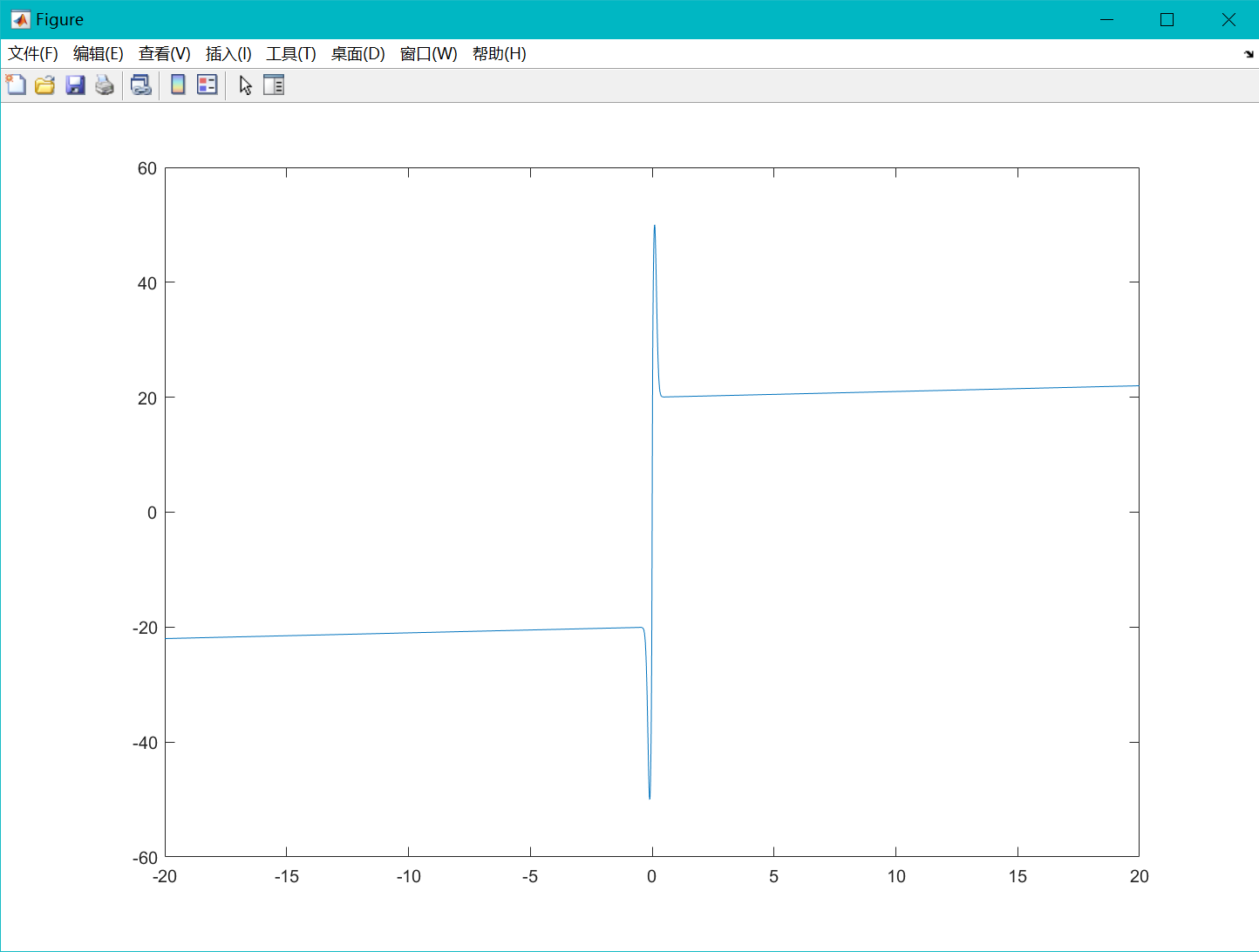
使用 matlab 的曲线拟合工具的自定义曲线拟合，结果如下：

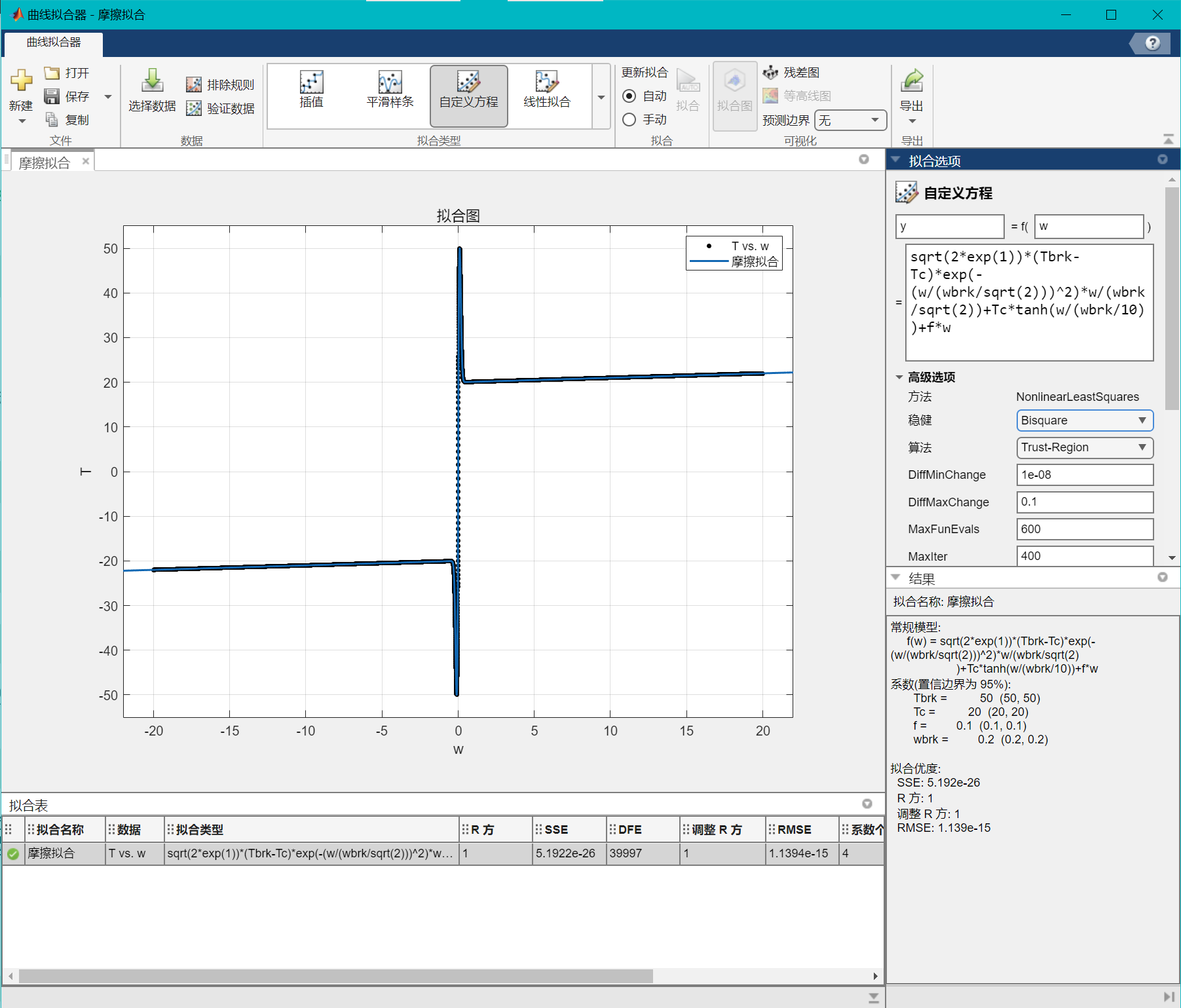
可以发现精度很好，牛的

代码参考：

• 摩擦拟合
• frictionCalibration

参考

引文

• @yoonFrictionModelingIdentification2014
• Friction in contact between rotating bodies - MATLAB - MathWorks 中国

脚注