Ch1 偏微分方程问题

Ch1 偏微分方程问题

波动方程

弦振动

问题建模如下：假定沿着 u 方向位移的函数为 $u(x,t)$，

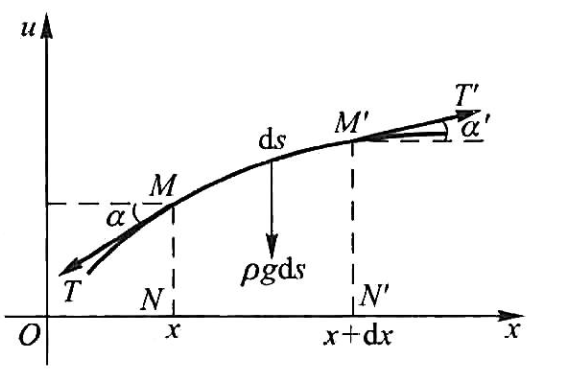
考虑水平方向力平衡：

$$T\cos \alpha =T^{\prime }\cos {\alpha }^{\prime }\Rightarrow T=T^{\prime }$$

考虑竖直方向力平衡，结合达朗贝尔原理：

$$\begin{array}{c}\frac{{\partial }^{2}u}{\partial t^2}\mathrm{d}m+T\sin \alpha +g\mathrm{d}m=T^{\prime }\sin {\alpha }^{\prime }\\ \Rightarrow \frac{{\partial }^{2}u}{\partial t^2}\rho \mathrm{d}s=T\left(\tan {\alpha }^{\prime }-\tan \alpha \right)-\rho g\mathrm{d}s\\ \Rightarrow \frac{{\partial }^{2}u}{\partial t^2}\rho \mathrm{d}s=T\left(\frac{\partial u\left(x+\mathrm{d}x,t\right)}{\partial x}-\frac{\partial u\left(x,t\right)}{\partial x}\right)-\rho g\mathrm{d}s\\ \Rightarrow \frac{{\partial }^{2}u}{\partial t^2}\rho =T\frac{{\partial }^{2}u}{\partial x^2}-\rho g\end{array}$$

忽略重力得到：

$$\frac{{\partial }^{2}u}{\partial t^2}=a^2\frac{{\partial }^{2}u}{\partial x^2},a=\sqrt{\frac{T}{\rho }}$$

这就是著名的 波动方程，这里是一维情形。补充受到外力作用情形时有：

$$\frac{{\partial }^{2}u}{\partial t^2}=a^2\frac{{\partial }^{2}u}{\partial x^2}+f\left(x,t\right),f\left(x,t\right)=\frac{1}{\rho }F\left(x,t\right)$$

这里 $f$ 代表 t 时刻单位质量的弦在 x 点处收到分布外力 F 作用下的外力密度。

note

注意，这里$F(x,t)$是分布外力，如果存在集中一点的力，可以使用狄拉克函数$\delta (x-x_0)$来代表，也就是说：

$$\begin{array}{c}\delta \left(x-x_0\right)=0,x\ne x_0\\ \delta \left(x-x_0\right)=\infty ,x=x_0\\ {\int }_{-\infty }^{\infty }\delta \left(x-x_0\right)\mathrm{d}x=1\end{array}$$

这里方程 (3) 和 (4) 之间的差别在于 (4) 右端多了一项与未知函数 u 无关的 f，这一项被称为 自由项，包含这种非零自由项的方程被称为 非齐次方程，自由项为 0 的被称为 齐次方程。

更进一步的，研究薄膜振动、声波空气中传播，可以得到二维 or 三维波动方程，如下式：

$$\begin{gathered} \frac{{\partial }^{2}u}{\partial t^2}=a^2\Delta u+f \\ \Delta u=\sum _{i=1}^n\frac{{\partial }^{2}u}{{\partial x_i}^2} \end{gathered}$$

其中 n 为维数，$\Delta$ 被称为 拉普拉斯算子。

电磁场方程

电磁场特性满足 麦克斯韦 方程组：

$$\begin{gathered} \mathbf{rot}\mathbf{H}=\mathbf{J}+\frac{\partial \mathbf{D}}{\partial \mathbf{t}} \\ \mathbf{rot}\mathbf{E}=-\frac{\partial \mathbf{B}}{\partial \mathbf{t}} \\ \mathbf{div}\mathbf{B}=0 \\ \mathbf{div}\mathbf{D}=\mathbf{\rho } \end{gathered}$$

其中 $J$ 代表传输电流的面密度，$\rho$ 代表电荷的体密度。

上面的方程结合下面场的物质方程：

$$\begin{gathered} \mathbf{D}=\mathbf{\epsilon E} \\ \mathbf{B}=\mathbf{\mu H} \\ \mathbf{J}=\mathbf{\sigma E} \end{gathered}$$

其中 $\epsilon$ 是介质的介电常数，$\mu$ 是磁导率，$\sigma$ 是电导率，假定介质时均匀且各向同的，那么此时 $\epsilon ，\mu ，\sigma$ 都是常数。

从上面两个式子中联立可以消除 H,E：

$$\begin{gathered} \Delta \mathbf{H}=\mathbf{\epsilon \mu }\frac{{\partial }^2\mathbf{H}}{\partial {\mathbf{t}}^2}+\mathbf{\sigma \mu }\frac{\partial \mathbf{H}}{\partial \mathbf{t}} \\ \Delta \mathbf{E}=\mathbf{\epsilon \mu }\frac{{\partial }^2\mathbf{E}}{\partial {\mathbf{t}}^2}+\mathbf{\sigma \mu }\frac{\partial \mathbf{E}}{\partial \mathbf{t}} \end{gathered}$$

如果介质不导电，那么 $\sigma =0$，有：

$$\begin{gathered} \frac{1}{\mathbf{\epsilon \mu }}\Delta \mathbf{H}=\frac{{\partial }^2\mathbf{H}}{\partial {\mathbf{t}}^2} \\ \frac{1}{\mathbf{\epsilon \mu }}\Delta \mathbf{E}=\frac{{\partial }^2\mathbf{E}}{\partial {\mathbf{t}}^2} \end{gathered}$$

这便是三维的波动方程。

泊松方程

式子 (7) 的后面两式可以导出静电场的点位满足的微分方程：

$$\begin{array}{c}\mathrm{div}D=\mathrm{div}\epsilon E=\epsilon \mathrm{div}E=\rho \\ E=-\mathrm{grad}u\\ \Rightarrow \mathrm{divgrad}u=-\frac{\rho }{\epsilon }\Rightarrow \Delta u=-\frac{\rho }{\epsilon }\end{array}$$

上面式子就是 泊松方程(Possion)，如果 $\rho =0$，即静电场无源，那么方程变为：

$$\Delta u=0$$

被称为 拉普拉斯方程

热传导方程

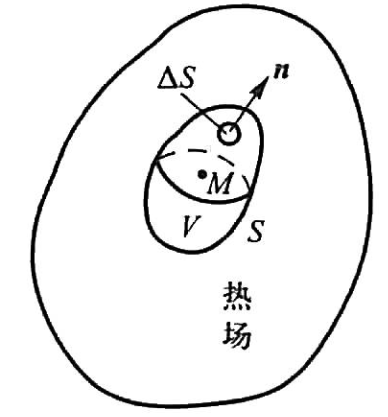
问题如上图所示，由传热学中 傅里叶实验定律 有，在时间段 $dt$ 内，通过面积微元 dS 的热量 dQ 与 s 时间 dt，曲面面积 dS，物体温度 u 沿着 dS 的法线方向导数成正比，有：

$$\begin{array}{c}dQ=-k\frac{\partial u}{\partial \mathbf{n}}dSdt\\ =-k{\left(\mathbf{grad}u\right)}_{\mathbf{n}}dSdt\\ =-k\mathbf{grad}u\cdot d\mathbf{S}dt,d\mathbf{S}=dS\mathbf{n}\end{array}$$

因此在一段时间内建立能量平衡有：

$${\iiint }_{V}c\rho \left[u\left(x,y,z,t_2\right)-u\left(x,y,z,t_1\right)\right]dV={\int }_{t_1}^{t_2}\left({\iint }_{S}k\mathbf{grad}u\cdot d\mathbf{S}\right)dt$$

左边的体积分可以写成：

$$\begin{array}{c}{\iiint }_{V}c\rho \left[u\left(x,y,z,t_2\right)-u\left(x,y,z,t_1\right)\right]dV\\ ={\iiint }_{V}c\rho \left[{\int }_{t_1}^{t_2}\frac{\partial u}{\partial t}dt\right]dV={\int }_{t_1}^{t_2}\left({\iiint }_{V}c\rho \frac{\partial u}{\partial t}dV\right)dt\end{array}$$

右边的面积分使用 高斯公式(Gauss) 将其化为三重积分：

$$\begin{gathered} {\iint }_{S}k\mathbf{grad}u\cdot d\mathbf{S}={\iiint }_{V}k\mathrm{div}\mathbf{grad}udV \\ ={\iiint }_{V}k\Delta udV \end{gathered}$$

因此有：

$$\begin{array}{c}{\int }_{t_1}^{t_2}\left({\iiint }_{V}c\rho \frac{\partial u}{\partial t}dV\right)dt={\int }_{t_1}^{t_2}{\iiint }_{V}k\Delta udVdt\\ \Rightarrow \frac{\partial u}{\partial t}=a^2\Delta u=a^2\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right),a^2=\frac{k}{c\rho }\end{array}$$

上式被称为 三维热传导方程

如果物体内部存在热源，那么需要添加自由项：

$$\frac{\partial u}{\partial t}=a^2\Delta u+f\left(x,y,z,t\right),f=\frac{F}{c\rho }$$

可以发现，如果时稳恒温度场，那么温度场与时间 t 无关，那么热传导方程转化为了拉普拉斯方程。

初值条件和边界条件

描述问题的条件存在两种形式，初值条件 和 边界条件

初值条件

• 弦振动类似的波动方程

  一般来说，这类方程的初值条件就是开始时刻的位移和速度，即：

$$\{\begin{array}{l}u{|}_{t=0}=\varphi \left(x\right)\\ \frac{\partial u}{\partial t}{|}_{t=0}=\psi \left(x\right)\end{array}$$

• 热传导方程

  初值条件指的是在开始时刻的物体温度分布情况，假设 $\varphi (M)$ 代表在 t=0 时刻物体内任意一点 M 的温度，那么热传导方程的初值条件为：

$$u\left(M,t\right){|}_{t=0}=\varphi \left(M\right)$$

• 泊松方程和拉普拉斯方程

  这两个方程描述的是稳恒状态的情况，因此不存在初值条件

边界条件

• 弦振动的波动方程

  一般存在三种端点约束类型：

  • 固定边界

    在弦振动过程中这个端点保持不动，这代表着边界条件：

$$u{|}_{x=a}=0$$

• 自由端

  这表示弦在这个端点不受位移方向的外力，从而在这个端点弦在位移返方向的张力为 0：

$$T\frac{\partial u}{\partial x}{|}_{x=a}=0\Rightarrow \frac{\partial u}{\partial x}{|}_{x=a}=0$$

• 弹性支撑端

  这表示弦在这个端点被某个弹性体所支撑，对端点使用胡克定律，有张力和外力平衡：

$$T\frac{\partial u}{\partial x}{|}_{x=a}=-ku{|}_{x=a}$$

• 热方程类似存在三种端点约束

• 总结

  • 第一类边界条件：$u{|}_{x=a}=f_1$

  • 第二类边界条件：$\frac{\partial u}{\partial x}{|}_{x=a}=f_2$

  • 第三类边界条件：$\left(\frac{\partial u}{\partial x}+\sigma u\right){|}_{x=a}=f_3$

  • 其中所有 $f_i$ 定义在边界 S 上，这些函数如果不依赖 u，那么称边界亦为齐次的，否则非齐次

定解问题

• 只有初值条件 (IC)，没有边界条件 (BC) 的问题称为 初值问题/柯西问题

• 只有 BC，没有 IC 的问题称为 边值问题

• BC+IC->混合问题

讨论偏微分方程的解从数学角度满足三个性质

• 解的存在性
• 解的唯一性
• 解的 稳定性

存在唯一稳定的解，那么问题为 适定的，By the way，一般的工程上偏微分问题都是适定的，已经证明

线性偏微分方程有一个重要性质：叠加原理

若 $u_i$ 是方程 $L{u}_i=f_i$ 的解，且级数 $u={\sum }_{i=1}^{\infty }{C}_i{u}_i$ 收敛，且可以逐项微分两次，$C_i$ 是任意常数，那么 $u$ 也是方程 $Lu={\sum }_{i=1}^{\infty }{C}_i{f}_i$ 的解

这一性质是 Ch2 分离变量法的基础 (事实上是线性空间那一套)